《机器学习实战》KMeans均值聚类算法
一、引言
聚类是一种无监督学习，对一些没有标签的数据进行分类。
二、K均值聚类算法
2.1 算法过程:
随机确定K个初始点为质心（簇个数k由用户给定），计算数据集中每个点到每个质心的距离
本次采用的是欧式距离，
完成后，每个簇的质心更新为该簇所有点的平均值。
进行迭代，直到相邻结果得到最终的质心误差在允许范围内。
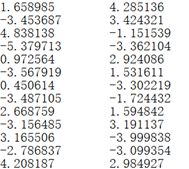
2.2 对testSet.txt进行数据可视化:
2.3 聚类结果（K=4）:+表示聚类中心点
2.4 后处理提高聚类性能
K是一个用户预先定义的参数，但我们并不清楚K的选择是否正确，也不知道这样生成的簇是否是最好的，如果有比较偏离的一小簇点，也会导致质心偏移，达不到好的聚类效果。
例如在书中10-2的图中，可以看出点的簇分类结果没有那么准确，原因是K均值算法收敛到了局部最小，而非全局最小值。
在包含簇分配结果的矩阵保存着每个点到簇质心的距离平方值，可以利用该值来评价聚类质量的方法。一类用于度量聚类效果的指标是SSE（误差平方和），对应我们在clusterAssment矩阵的第一列之和，SSE值越小表明数据点接近于他们的质心，聚类效果越好。
图10-2
这里介绍一下误差平方和：
对象
误差的平方和表示为：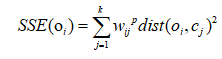
参数
控制隶属度的影响.p的值越大，隶属度影响越大。
由于一个对象可能参与多个簇，所以用隶属度加权到簇中心的距离之和代表对象拟合聚类的程度。
簇 
的SSE是：
聚类C的SSE的定义：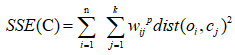
，用来度量模糊聚类对数据集合的拟合程度
对图10-2的优化：
将具有最大SSE的簇划分为两个簇，实现时可以将最大簇包含的点过滤出来并在这些点上运行K均值算法，K=2。
为了保证簇的总数不变，可以将某两个簇进行合并。
对原图中即是，将两个出错的质心进行合并。
那么在多维空间中如何合并最近的质心呢？我们可以计算所有质心之间的距离，然后合并距离最近的两个点来实现，又或者合并两个簇后计算两次总SSE值，在所有簇上重复执行，知道找到合并最佳的两个簇。
2.3 K均值聚类主函数程序
def kMeans(dataSet, k, distMeas=distEclud,createCent=randCent):
m= shape(dataSet)[0]
clusterAssment = mat(zeros((m,2)))#create mat to assign data points
#存储每个点的簇分配结果（两列，存储簇索引值，存储误差（当前点到簇质心的距离））
centroids = createCent(dataSet, k)
clusterChanged = True #标志变量，true就继续迭代
while clusterChanged:
clusterChanged = False
for i in range(m):#for each data point assign it to the closest centroid
minDist = inf; minIndex = -1
for j in range(k):
distJI =distMeas(centroids[j,:],dataSet[i,:])
if distJI < minDist:
minDist = distJI; minIndex= j
if clusterAssment[i,0] != minIndex: clusterChanged = True
clusterAssment[i,:] = minIndex,minDist**2
print(centroids)
for cent in range(k):#recalculate centroids
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A==cent)[0]]#get allthe point in this cluster
centroids[cent,:] = mean(ptsInClust, axis=0) #assign centroid to mean
return centroids, clusterAssment
三、二分K均值算法
3.1 算法原理
为了克服K均值收敛于局部最小值，二分K均值算法首先将所有点作为一个粗，然后将簇一分为二，之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值，基于SSE的划分过程不断重复，直到得到用户指定的簇数目为止。
3.2 对testSet2.txt数据集进行测试
得到最终的质心结果：centList
画图：
得到较好的聚类效果。
3.3 实验代码
def biKmeans(dataSet, k,distMeas=distEclud):
m= shape(dataSet)[0]
clusterAssment = mat(zeros((m,2)))
centroid0= mean(dataSet, axis=0).tolist()[0]
centList =[centroid0] #create a list with one centroid
for j in range(m):#calc initial Error
clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
while (len(centList) < k):
lowestSSE = inf
for i in range(len(centList)):
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]#getthe data points currently in cluster i
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
sseSplit = sum(splitClustAss[:,1])#compare the SSE to the currrentminimum
sseNotSplit =sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
print("sseSplit, and notSplit: ",sseSplit,sseNotSplit)
if (sseSplit + sseNotSplit)< lowestSSE:
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss =splitClustAss.copy()
lowestSSE = sseSplit +sseNotSplit
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList)#change 1 to 3,4, or whatever
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
print('the bestCentToSplit is: ',bestCentToSplit)
print('the len of bestClustAss is: ', len(bestClustAss))
centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0]#replace acentroid with two best centroids
centList.append(bestNewCents[1,:].tolist()[0])
clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]=bestClustAss#reassign new clusters, and SSE
return mat(centList), clusterAssment
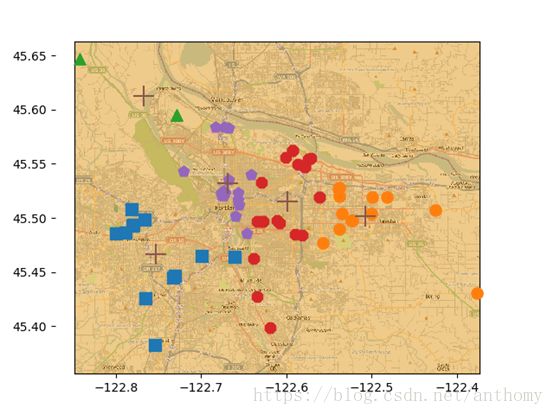
四、程序实例（对地图上的点聚类）
4.1 采用算法：二分K均值
数据集：地图
4.2 使用Yahoo PlaceFinder API获得地图上的每个点的经纬度
4.3 实验结果
五、总结与体会
优点：容易实现
缺点：可能收敛到局部最小值，在大规模数据集上收敛较慢
六、参考文献
【1】《机器学习实战》Peter Harrington
【2】《数据挖掘-概念与技术》JiaWei Han、Micheline Kamber、Jian Pei
非常感谢阅读！如有不足之处，请留下您的评价和问题。