深度学习（二）——深度学习常用术语解释, Neural Network Zoo, CNN, Autoencoder

Dropout（续）

除了Dropout之外，还有DropConnect。两者原理上类似，后者只隐藏神经元之间的连接。

总的来说，Dropout类似于机器学习中的L1、L2规则化等增加稀疏性的算法，也类似于随机森林、模拟退火之类的增加随机性的算法。

参考：

https://zhuanlan.zhihu.com/p/23178423

Dropout解决过拟合问题

深度学习常用术语解释

深度学习中epoch、batch size、iterations的区别

one epoch：所有的训练样本完成一次Forword运算以及一次BP运算。

batch size：一次Forword运算以及BP运算中所需要的训练样本数目，其实深度学习每一次参数的更新所需要损失函数并不是由一个{data：label}获得的，而是由一组数据加权得到的，这一组数据的数量就是[batch size]。当然batch size越大，所需的内存就越大，要量力而行。

iterations（迭代）：每一次迭代都是一次权重更新，每一次权重更新需要batch size个数据进行Forward运算得到损失函数，再BP算法更新参数。

最后可以得到一个公式one epoch = numbers of iterations = N = 训练样本的数量/batch size

Vanilla

Vanilla是神经网络领域的常见词汇，比如Vanilla Neural Networks、Vanilla CNN等。Vanilla本意是香草，在这里基本等同于raw。比如Vanilla Neural Networks实际上就是BP神经网络，而Vanilla CNN实际上就是最原始的CNN。

weight decay

weight decay（权值衰减）的使用既不是为了提高收敛精确度，也不是为了提高收敛速度，其最终目的是防止过拟合。在损失函数中，weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，若weight decay很大，则复杂的模型损失函数的值也就大。

https://mp.weixin.qq.com/s/W4d2fkiJig–PuDPM11ozA

Batch Normalization

Batch Normalization是Google提出的一种神经网络优化技巧。

原始论文：

《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》

上图是Hinton在2015年的讲座中的例子。从中可以看出，反向传递的梯度大小不仅和激活函数有关，也和每一层的权值大小有关。

通常来说，越靠近输出层，由于该层网络已被充分训练，其权值越大，反之则越小。这实际上也是梯度消失的一种原因。

更一般的，如果一层的权值显著异于相邻的层，从系统的角度出发，这一层也是不稳定的。Batch Normalization将各层的权值归一化，从而改善了神经网络的性能。它的优点有：

1.提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1]，这样在反向传播时候的梯度都是在1左右，避免了梯度消失现象。

2.提升学习速率。归一化后的数据能够快速的达到收敛。

3.减少模型训练对初始化的依赖。

类似的概念还有Weight Normalization和Layer Normalization。

以下是它们的特点：

Batch Normalization

对于batch size比较小的时候，效果非常不好，而batch size越大，那么效果则越好，因为其本质上是要通过mini-batch得到对整个数据集的无偏估计；

在训练阶段和推理阶段的计算过程是不一样的；

在CNN上表现较好，而不适用于RNN甚至LSTM

Weight Normalization

计算简单，易于理解

相比于其他两种方法，其训练起来不太稳定，非常依赖于输入数据的分布。

Layer Normalization

不依赖于batch size的大小，即使对于batch size为1的在线学习，也可以完美适应；

训练阶段和推理阶段的计算过程完全一样。

适用于RNN或LSTM，而在CNN上表现一般。

参考：

http://www.cnblogs.com/neopenx/p/5211969.html

从Bayesian角度浅析Batch Normalization

https://www.zhihu.com/question/38102762

深度学习中 Batch Normalization为什么效果好？

http://jiangqh.info/Batch-Normalization%E8%AF%A6%E8%A7%A3/

Batch Normalization详解

https://mp.weixin.qq.com/s/OAn8y_uJTgyrtS2ZCyudlg

Batch Normalization原理及其TensorFlow实现

https://mp.weixin.qq.com/s/EBRYlCoj9rwf0NQY0B4nhQ

Layer Normalization原理及其TensorFlow实现

鞍点

鞍点（Saddle point）在微分方程中，沿着某一方向是稳定的，另一条方向是不稳定的奇点，叫做鞍点。在泛函中，既不是极大值点也不是极小值点的临界点，叫做鞍点。在矩阵中，一个数在所在行中是最大值，在所在列中是最小值，则被称为鞍点。在物理上要广泛一些，指在一个方向是极大值，另一个方向是极小值的点。

上图是 z=x2−y2 的曲面图，其中的原点就是鞍点。上图形似马鞍，故名。

LeCun和Bengio的研究表明，在high-D(高维)的情况下，局部最小会随着维度的增加，指数型的减少，在深度学习中，一个点是局部最小的概率非常小，同时鞍点无处不在。

欠拟合和过拟合

在DL领域，欠拟合意味着神经网络没有学到该学习的特征，而过拟合则意味着神经网络学习到了不该学习的特征。

在之前的描述中，我们一直强调过拟合的风险，然而实际上，欠拟合才是DL最大的敌人。

首先，神经网络对于学习样本数量的要求非常高，基本比浅层模型多2～3个数量级，因此过拟合的风险并不太大。

其次，过拟合的危害也没有欠拟合那么高。比如下面的场景：

1.对同一训练样本集 T1 ，进行两次训练，分别得到模型 M1,M2 。

2.使用 M1,M2 对同一测试样本集 T2 进行预测，得到预测结果集 P1,P2 。

3.如果 P1,P2 的结论基本相反的话，则说明发生了欠拟合现象。而过拟合则并没有这么夸张的效果。

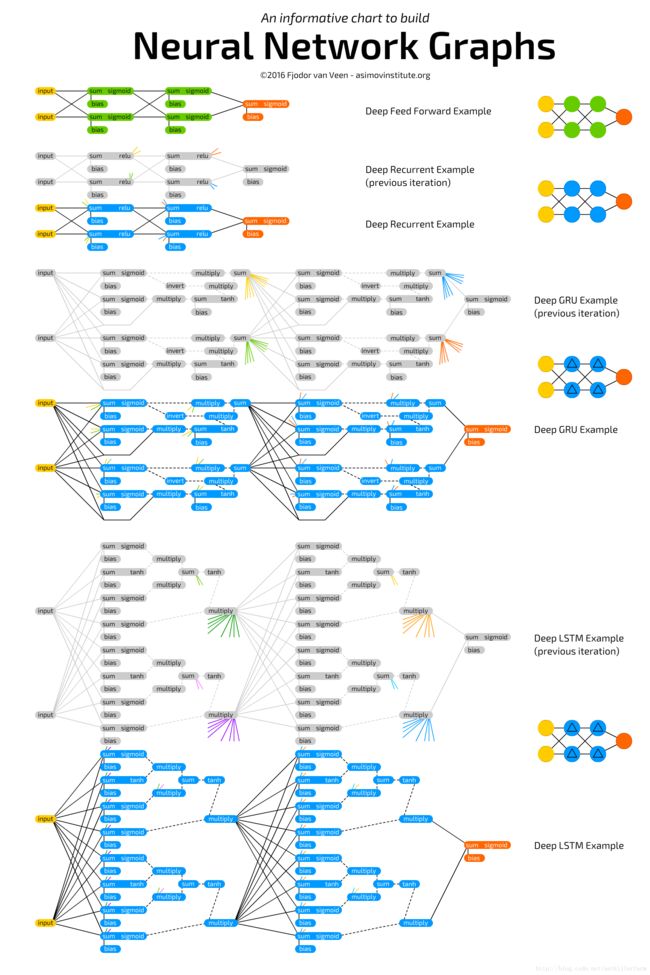
Neural Network Zoo

在继续后续讲解之前，我们首先给出常见神经网络的结构图：

上图的原地址为：

http://www.asimovinstitute.org/neural-network-zoo/

单元结构：

层结构：

上图的原地址为：

http://www.asimovinstitute.org/neural-network-zoo-prequel-cells-layers/

CNN

概述

卷积神经网络（Convolutional Neural Networks，ConvNets或CNNs）属于神经网络的范畴，已经在诸如图像识别和分类的领域证明了其高效的能力。

CNN的开山之作是Yann LeCun的论文：

《Gradient-Based Learning Applied to Document Recognition》

注：科学界的许多重要成果的开山之作，其名称往往和成果的最终名称有一定的差距。比如LeCun的这篇文章的名称中，就没有CNN。类似的还有Vapnik的SVM，最早被称为Support Vector Network。

英文不好的，推荐以下文章：

http://www.hackcv.com/index.php/archives/104/

CNN的直观解释

关键点

这里以最经典的LeNet-5为例，提点一下CNN的要点。

LeNet-5的caffe模板：

https://github.com/BVLC/caffe/blob/master/examples/mnist/lenet.prototxt

卷积

在《数学狂想曲（五）》中我们讨论了卷积的数学含义，结合《 图像处理理论（一）》和《 图像处理理论（二）》，不难看出卷积或者模板（算子），在前DL时代，几乎是图像处理算法的基础和灵魂。为了实现各种目的，人们手工定义或发现了一系列算子。

到了DL时代，卷积仍然起着非常重要的作用。但这个时候，不再需要人工指定算子，算子本身也将由学习获得。我们需要做的只不过是指定算子的个数而已。

比如，LeNet-5的C1:6@28*28，其中的6就是算子的个数。显然算子的个数越多，计算越慢。但太少的话，又会导致提取的特征数太少，神经网络学不到东西。

除此之外，卷积还包含了图片的空间二维信息，它和后面的Pooling操作一道，起到了空间降维的作用。

实际上，传统的MLP（MultiLayer Perceptron）网络，就是由于1D全连接的神经元控制了太多参数，而不利于学习到稀疏特征。

CNN网络中，2D全连接的神经元则控制了局部感受野，有利于解离出稀疏特征。

池化

Pooling操作（也称Subsampling）使输入表示（特征维度）变得更小，并且网络中的参数和计算的数量更加可控的减小，因此，可以控制过拟合。

它还可使网络对于输入图像中更小的变化、冗余和变换变得不变性。

Gaussian Connections

LeNet-5最后一步的Gaussian Connections是一个当年的历史遗迹，目前已经被Softmax所取代。它的含义在上面提到的Yann LeCun的原始论文中有描述。

其他

上图展示了不同分类的图片特征在特征空间中的分布，可以看出在CNN的低层中，这些特征是混杂在一起的；而到了CNN的高层，这些特征就被区分开来了。

上图是若干ML、DL算法按照不同维度划分的情况。

CNN的反向传播算法

由于卷积和池化两层，不是一般的神经网络结构。因此CNN的反向传播算法实际上也是很有技巧的。

参见：

http://www.cnblogs.com/pinard/p/6494810.html

卷积神经网络(CNN)反向传播算法

卷积的反向传播，有时也被称为反卷积。

上图是Deep convolutional inverse graphics networks的结构图。DCIGN实际上是一个正向CNN连上一个反向CNN，以实现图片合成的目的。

参考

http://lib.csdn.net/article/deeplearning/58185

BP神经网络与卷积神经网络

http://blog.csdn.net/Fate_fjh/article/details/52882134

卷积神经网络系列blog

http://mp.weixin.qq.com/s/YRwGwelyA3VOYZ4XGAjUBw

CNN 感受野首次可视化：深入解读及计算指南

http://mp.weixin.qq.com/s/dvuX3Ih_DZrv0kgqFn8-lg

卷积神经网络结构变化——可变形卷积网络deformable convolutional networks

Autoencoder

Bengio在2003年的《A neural probabilistic language model》中指出，维度过高，会导致每次学习，都会强制改变大部分参数。

由此发生蝴蝶效应，本来很好的参数，可能就因为一个小小传播误差，就改的乱七八糟。

因此，数据降维是数据预处理中，非常重要的一环。常用的降维算法，除了线性的PCA算法之外，还有非线性的Autoencoder。

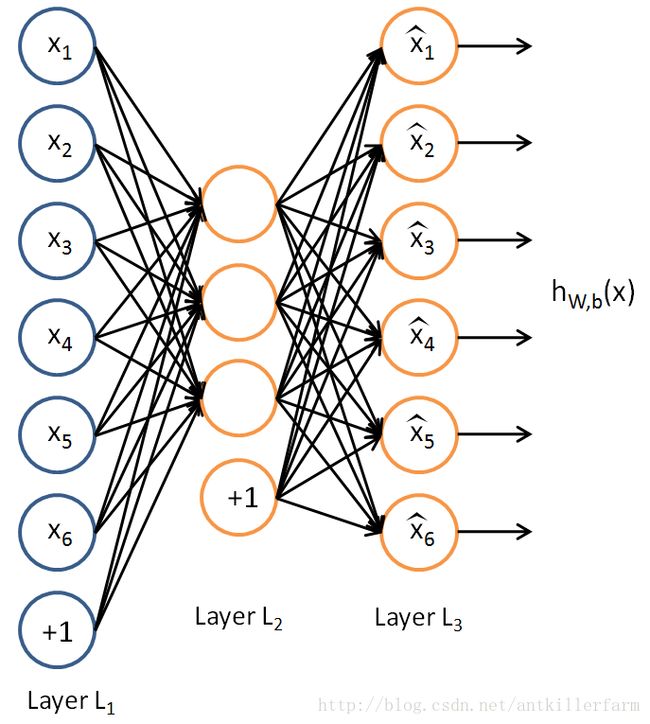
Autoencoder的结构如上图所示。它的特殊之处在于：

1.输入样本就是输出样本。

2.隐藏层的神经元数量小于样本的维度。