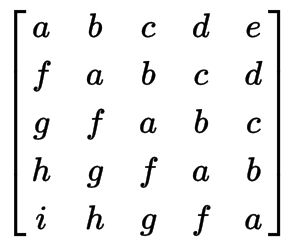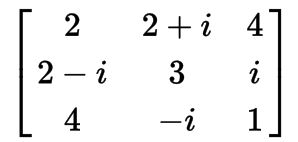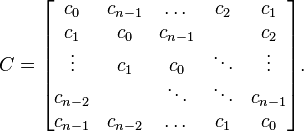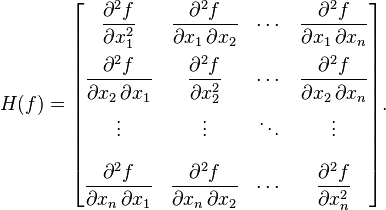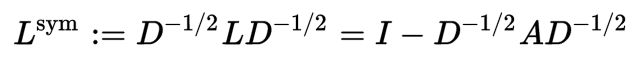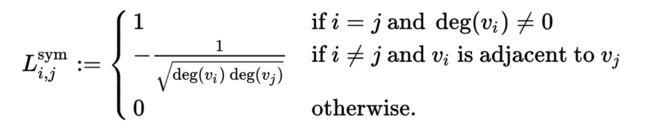数学中的各种矩阵大总结
1、单位矩阵(Identity Matrix)
如果A矩阵可逆,其逆矩阵为A-1,那么AA-1 = I,这里 I 就是单位矩阵。形式上,单位矩阵 I 是一个n×n的方阵,其主对角线上的元素都是1,其余位置的元素都为0。因此,单位矩阵也可以记为: In = diag(1, 1, ..., 1)。
2、上三角矩阵/下三角矩阵
在线性代数中,三角矩阵是方形矩阵的一种,如下图所示,该矩阵的下三角(不包括主对角线)的元素均为常数0,则称其为一个上三角矩阵。
与上三角矩阵相反,如果一个矩阵的主对角线上方均为常数0,则称该矩阵为下三角矩阵,例如:
3、Toeplitz 矩阵
Toeplitz矩阵又叫做常对角矩阵(diagonal-constant matrix),指矩阵中每条自左上至右下的斜线上之元素都为同一常数的矩阵。例如下面就是一个Toeplitz矩阵的例子:
任意n×n的Toeplitz矩阵具有如下形式:
最常见的Toeplitz矩阵是对称Toeplitz矩阵,这种矩阵仅由第一行元素就可以完全确定。
4、Hermitian 矩阵
对于一个复矩阵A,其共轭转置记为A*。如果A = A*,则称为Hermitian矩阵。例如,
显然,如果一个实矩阵是对称的,那么它也是一个Hermitian矩阵。
此外,如果一个复Toeplitz矩阵中之元素满足复共轭对称关系,则称其为Hermitian Toeplitz矩阵。
5、循环矩阵(Circulant Matrix)
循环矩阵是Toeplitz矩阵的一种特殊形式,如下所示,当给定矩阵的第一行时,矩阵的后一行都是由前一行向右循环移位得到的。
6、酉矩阵(Unitary Matrix)与正交矩阵
A ∈ Mn×n(C), A*A = AA* = I, then A is unitary; A ∈ Mn×n(R), ATA = AAT = I, then A is orthogonal。
7、Hessian 矩阵
形如下面样子的矩阵,具体请参考《Hessian矩阵与多元函数极值》。
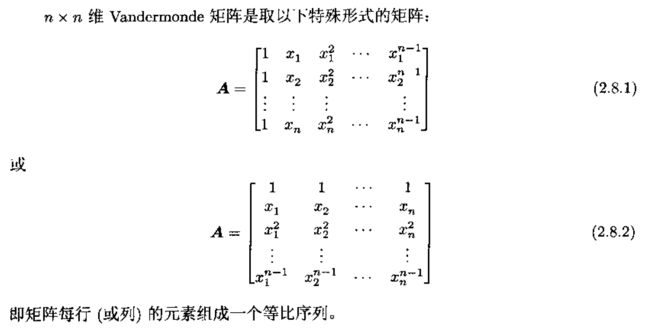
8、Vandermonde 矩阵
10、拉普拉斯矩阵(Laplacian matrix)
拉普拉斯矩阵是图论中用到的一种重要矩阵,给定一个有n个顶点的图 G=(V,E),其拉普拉斯矩阵被定义为 L = D-A,其中为图的度矩阵,为图的邻接矩阵。例如,给定一个简单的图,如下(例子来自wiki百科):
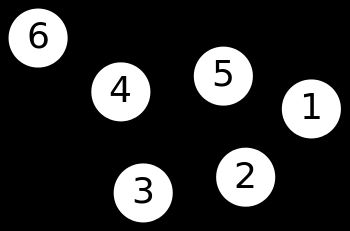
把此“图”转换为邻接矩阵的形式,记为A:

把W的每一列元素加起来得到N个数,然后把它们放在对角线上(其它地方都是零),组成一个N×N的对角矩阵,记为度矩阵D,如下图所示。其实度矩阵(对角线元素)表示的就是原图中每个点的度数,即由该点发出的边之数量。

根据拉普拉斯矩阵的定义L = D-A,可得拉普拉斯矩阵L 为:

显然,拉普拉斯矩阵都是对称的。此外,另外一种更为常用的拉普拉斯矩阵形式是正则化的拉普拉斯矩阵(Symmetric normalized Laplacian),定义为:
该矩阵中的元素由下面的式子给出:
附录、循环矩阵的对角化
前面Part 5中介绍的循环矩阵有一个很特殊的性质,即它可以被Fourier矩阵对角化,即有:
* 8-9 来自《矩阵分析与应用》(张贤达 著)
* 补充循环矩阵对角化的一个英文资料 (Iterative Methods for Toeplitz Systems, Michael K. Ng, Oxford University Press)
(本文完)