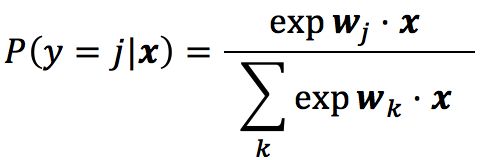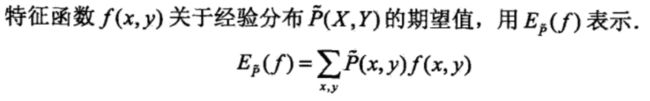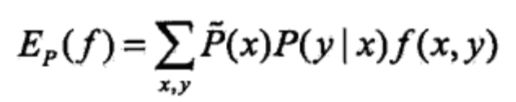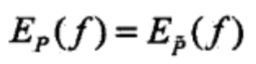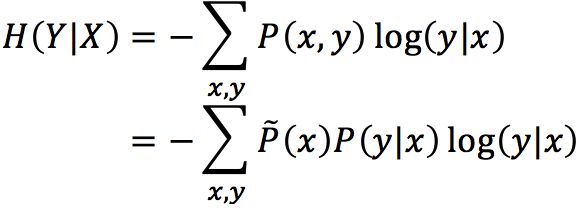最大熵模型(MaxEnt):万法归宗(上)
引言:文献【1】中第88页,给出了最大熵模型的一般形式(其中的f为特征函数,后面我们还会讲到):
而文献【5】中我们从另外一种不同的角度也得出了多元逻辑回归的一般形式:
可见,尽管采用的方法不同,二者最终是殊途同归、万法归宗了。 所以我们说无论是多元逻辑回归,还是最大熵模型,又或者是Softmax,它们本质上都是统一的。本文就将从最大熵原理这个角度来推导上述最大熵模型的一般形式。
最大熵原理
首先,关于熵这个概念的一些解读,可以参考【6】和【7】。简单地说,假设离散随机变量X的概率分布是P(X),则其熵是
而且熵满足下列不等式:
0≤H(P)≤log|X|
其中,|X|是X的取值个数,当且仅当X的分布是均匀分布时右边的等号成立。也就是说,当X服从均匀分布时,熵最大。
直观地,最大熵原理认为要选择的概率模型首先必须满足已有的事实,即约束条件。在没有更多信息的情况下,那些不确定的部分都是“等可能的”。最大熵原理通过熵的最大化来表示等可能性。“等可能性”不容易操作,而熵则是一个可以优化的数值指标。
吴军博士在其所著的《数学之美》一书中曾经谈到:“有一次,我去AT&T实验室作关最大熵模型的报告,随身带了一个骰子。我问听众‘每个面朝上的概率分別是多少’,所有人都说是等概率,即各种点数的概率均为1/6。这种猜测当然是对的。我问听众为什么,得到的回答是一致的:对这个‘一无所知’的骰子,假定它毎一面朝上概率均等是最安全的做法。(你不应该主观假设它像韦小宝的骰子—样灌了铅。)从投资的角度看,就足风险最小的做法。从信息论的角度讲,就足保留了最大的不确定性,也就是说让熵达到最大。
接着我又告诉听众,我的这个骰子被我特殊处理过,已知四点朝上的概率是1/3,在这种情况下,每个面朝上的概率是多少?这次,大部分人认为除去四点的概率是1/3,其余的均是2/15,也就是说已知的条件(四点概率为1/3)必须满足,而对于其余各点的概率因为仍然无从知道,因此只好认为它们均等。注意,在猜测这两种不同情况下的概率分布时,大家都没有添加任何主观的假设,诸如四点的反面一定是三点等等。(事实上,有的骰子四点的反面不是三点而是一点。)这种基于直觉的猜测之所以准确,是因为它恰好符合了最大熵原理。”
通过上面关于骰子的例子,我们对最大熵原理应该已经有了一个基本的认识,借用文献【8】中的话就是“model all that is known and assume nothing about that which is unknown”。
约束条件
最大熵原理是统计学习理论中的一般原理,将它应用到分类任务上就会得到最大熵模型。假设分类模型是一个条件概率分布P(Y|X),X ∈ Input ⊆ Rn表示输入(特征向量),Y∈ Output 表示输出(分类标签),Input和Output分别是输入和输出的集合。这个模型表示的是对于给定的输入X,输出为Y的概率是P(Y|X)。
给定一个训练数据集
我们现在的目标是利用最大熵原理来选择最好的分类模型。首先来考虑模型应该满足的条件。给定训练数据集,便可以据此确定联合分布P(X,Y)的经验分布![]() ,以及边缘分布P(X)的经验分布
,以及边缘分布P(X)的经验分布![]() 。关于经验分布,你可以参考【4】以了解更多。此处,我们有
。关于经验分布,你可以参考【4】以了解更多。此处,我们有
其中,v(X=x, Y=y)表示训练数据集中样本(x,y)出现的频率(也就是计数);v(X=x)表示训练数据集中输入x出现的频率(也就是计数),N是训练数据集的大小。
举个例子,在英汉翻译中,take有多种解释例如下文中存在7种:
在没有任何限制的条件下,最大熵原理认为翻译成任何一种解释都是等概率的,即
P(t1|x)=P(t2|x)=...=P(t7|x)=1/7
实际中总有或多的限制条件,例如t1,t2比较常见,假设满足
P(t1|x)+P(t2|x)=2/5
同样根据最大熵原理,可以得出
P(t1|x)=P(t2|x)=1/5
P(t3|x)=P(t4|x)=P(t5|x)=P(t6|x)=P(t7|x)=3/25
通常可以用特征函数f(x,y)来描述输入x和输出y之间的某一个事实。一般来说,特征函数可以是任意实值函数,下面我们采用一种最简单的二值函数来定义我们的特征函数
它表示当x和y满足某一事实时,函数取值为1,否则取值为0。
实际的统计模型中,我们通过引入特征(以特征函数的形式)提高准确率。例如take翻译为乘坐的概率小,但是当后面跟着交通工具的名词“bus",概率就变得非常大。于是有
同理,Ep( f )表示f(x,y)在模型上关于实际联合分布P(X,Y)的数学期望,类似地则有
注意到P(x,y)是未知的,而建模的目标是生成P(y|x),因此我们希望将P(x,y)表示成P(y|x) 的函数。于是,利用贝叶斯公式,有P(x, y)=P(x)P(y|x),但P(x)仍然是未知的。此时,只得利用![]() 来近似。于是,我们便可以将Ep( f )重写成
来近似。于是,我们便可以将Ep( f )重写成
对于概率分布P(y|x),我们希望特征函数f的期望 应该与 从训练数据集中得到的特征期望值相一致,因此提出约束:
即
我们把上式作为模型学习的约束条件。假如有n个特征函数 fi(x,y),i=1,2,...,n,那么就相应有n个约束条件。
最大熵模型
给定训练数据集,我们的目标是:利用最大熵原理选择一个最好的分类模型,即对于任意给定的输入x ∈ Input,可以以概率P(y|x)输出y ∈ Output。要利用最大熵原理,我们还需要一个熵的定义。由于我们的目标是获取一个条件分布,因此要采用相应的条件熵H(Y|X),或者记作H(P),更多关于条件熵的细节可以参考【9】
至此,我们就可以给出最大熵模型的完整描述了。对于给定的训练数据集以及特征函数 fi(x,y),i=1,2,...,n,最大熵模型就是求解
或者按照最优化问题的习惯,可以将上述求最大值的问题等价地转化为下面这个求最小值的问题:
其中的条件∑P(y|x)=1是为了保证P(y|x)是一个合法的条件概率分布。
现在便得到了一个带等式约束的最优化问题,显然需要使用拉格朗日乘数法。这部分数学推导,我们留到下一篇文章中再详细介绍。
【1】李航,统计学习方法,清华大学出版社
【2】https://www.cnblogs.com/wxquare/p/5858008.html
【3】http://blog.csdn.net/itplus/article/details/26550273
【4】经验分布函数(Empirical Distribution Functions)
【5】http://blog.csdn.net/baimafujinji/article/details/51703322
【6】http://blog.csdn.net/baimafujinji/article/details/6469645
【7】http://blog.csdn.net/baimafujinji/article/details/6471675
【8】Adam Berger. A Brief Maxent Tutorial, 1996
【9】图像处理中的数学修炼,清华大学出版社
(本文完)