排序算法总结Sorting Algo

Backto Algo Index

综述

对于一个 Sorting Algo 的评价，一般有以下几个标准

1. Time Complexity：Best，Worst, Average
   不仅要知道三个时间复杂度，还要知道对应的数据情形。通常对于基于比较的 Sorting Algo，Best 就是顺序排列的，Worst 就是 逆序排列的，Average 就是随机排列的。因为不同的 Algo 在不同的情形下表现可能大不同个，因为我们需要根据业务的实际情况，pick the right one.
2. 时间复杂度的系数，常数，低阶
   当用 Big-O 分析的时候，通常忽略这些细节，但是 Big-O 针对的是数据规模很大的情况下的增长趋势。而排序算法，很多情况下是限定规模的， 比如 10， 1000， 100万，因此这些被忽略的项需要加上才能比较不同algo 的优劣。
3. 比较次数和交换（或移动）的次数
   尤其是对于基于比较的排序算法，核心就两步，比较–交换， 统计次数尤为重要。
4. algo 的内存消耗
   也就是空间复杂度啦，如果是原地排序（sorted in place），空间复杂度就是 $O(1)$.
5. algo 的稳定性
   一个sorting algo 具有稳定性指的是，排序前后相等的元素相对位置不变。否则，就是不稳定的 sorting algo。例如对于一组数据3,5,6,3,1, 排序后是1,3,3,5,6 这里面两个相等的 3 相对位置是否改变了,决定了使用的algo 是否具有稳定性. 这个在实际业务中很重要, 因为我们总是需要根据多个不同的度量多层次排序, 可不希望一个层次排好了,其他层次全乱了.

经典的排序算法

Sorting Algo	Time Complexity	Based on comparsion?	DESC
BubbleSort 冒泡排序	$O(n^2)$	Yes	依次比较, 大的往后换
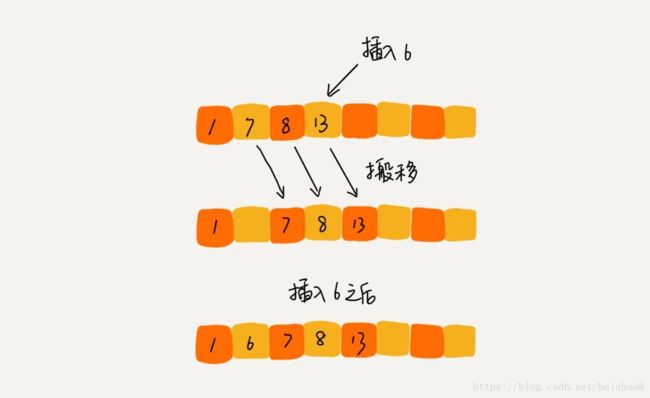
InsertionSort 插入排序	$O(n^2)$	Yes	左边已排序,右边未排序.把未排序部分依次insert到排序部分中去
SelectionSort 选择排序	$O(n^2)$	Yes	左边已排序,右边未排序.在右边select最小值,和右边第一个数swap.左边+1,右边-1.
QuickSort 快排	$O(n\log n)$	Yes	在数组的头尾之间任意选取一个pivot,然后遍历数组小于pivot的放左边,大于pivot的放右边.pivot居中间.然后左右再分别QuickSort.
MergeSort 归并排序	$O(n\log n)$	Yes	打散成小组,小组排好序. 再把小组结果merge成完整的排序序列.
BucketSort 桶排序	$O(n)$	No
CountingSort 计数排序	$O(n)$	No
RadixSort 基排序	$O(n)$	No

BubbleSort

void Swap(int& a, int& b) {
	int temp = a;
	a = b;
	b = temp;
}

//the bigger one move backward
void BubbleSort(int* a, int n) {
	if(n <= 1)
		return;
	bool hasSorted = true;
	for (int i = 0; i < n; ++i) { //controls bubble times
		for (int j = 0; j < n-1-i; ++j) { // move the biger backward
			if (a[j+1]>a[j]) {
				Swap(a[j+1], a[j]);
				hasSorted = false;
			}
		}
		if (hasSorted)
			break;
	}
}

InsertionSort

// Pick element in unsorted region and Insert it Into sorted region 
void InsertionSort(int* a, int n) {
	if(n <= 1)
		return;
	for(int i = 1; i < n; ++i) { //the 1st is in order, insert the last (n-1) elements
		int value = a[i]; // value to insert
		int j = i -1;
		for(;j>=0;--j) { //compare with left elements to find the insertion postion
			if(a[j] > value) { // greater than value
				a[j+1] = a[j]; //move right-ward
			} else { //less than value
				break; // pos to insert is found = (j+1), stop moving
			}
		}
		a[j+1] = value;
	}
}

SelectionSort

// Select the smallest element from the unsorted region and 
// append it to the tail of sorted region.
// unstable, less used
void  SelectionSort(int* a, int n) {

}

MergeSort

//interface
void MergeSort(int* a, int n) {
	MergeSort(a, 0, n-1);
}
//real worker
void MergeSort(int* a, int idx_head, int idx_tail) {
	//terminate condition
	if(idx_head >= idx_tail)
		return;
	//find the middle pos
	int idx_mid = (idx_head + idx_tail)/2;
	//divide into 2 sub-tasks with recursion
	MergeSort(a, idx_head, idx_mid);
	MergeSort(a, idx_mid+1, idx_tail);
	//merge results
	Merge(a, idx_head, idx_mid, idx_tail);
}
// Merge phase
void Merge(int* a, int idx_head, int idx_mid, int idx_tail) {
	int i = idx_head; //  iter over elems in the 1st part
	int j = idx_mid + 1; //  iter over elems in the 2nd part
	int k = 0; // iter over tmp array
	int* tmp = new int[idx_tail - idx_head + 1];
	while(i <= idx_mid && j <= idx_tail) { // either one hits the end, stop comp
		if(a[i] > a[j]) // NOT `>=`. if `=` is added, the algo is not stable anymore
			tmp[k++] = a[j++];
		else
			tmp[k++] = a[i++];
	}
	//judge which array remains elems
	int head = i; // 1st array remains
	int end = idx_mid;
	if(j <= idx_tail) { //2nd array remains
		head = j;
		end = idx_tail;
	}
	//copy remained elems
	while(start <= end)
		tmp[k++] = a[start++];
	// copy tmp back to a
	for(i=0; i <= idx_tail- idx_head; ++i)
		a[i] = tmp[i];
	SafeDelete(tmp);
}

QuickSort

//public interface
void QuickSort(int* a, int n) {
	QuickSort(a, 0, n-1);
}
// real worker
void QuickSort(int* a, int idx_head, int idx_tail) {
	if(idx_head >= idx_tail)
		return;
	int idx_mid = Partition(a, idx_head, idx_tail);
	QuickSort(a, idx_head, idx_mid);
	QuickSort(a, idx_mid+1, idx_tail);
}
//Version 1: Clear, Short, 
// e.g.
// a = [5,1,4,2,3], idx_head=0, idx_tail=4
// j = 0, do nothing, 5-1-4-2-3, i = 0;
// j=1, swap(a[0], a[1]), 1-5-4-2-3, i=1;
// j=2, do nothing, 1-5-4-2-3, i=1;
// j=3, swap(a[1],a[3]), 1-2-4-5-3, i=2;
// iter over, i=2, swap(a[2],a[4]), 1-2-3-5-4, i=2
// return 2
int Partition(int* a, int idx_head, int idx_tail) {
	int pivot = a[idx_tail]; 
	int i = idx_head; //iter grows to find the mid
	int j = idx_head; //iter over a to find elems less than pivot
	for(; j < idx_tail; ++j) {
		if(a[j] < pivot) { // find an elem less than pivot
			Swap(a[i], a[j]); //swap it front
			++i; //smaller elems count + 1
		}
	}
	Swap(a[i], a[idx_tail]);
	return i;
}