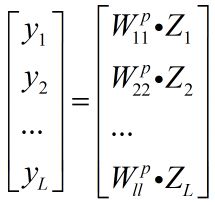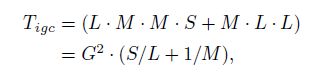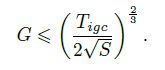深度学习10篇文章之Interleaved Group Convolution
本文主要讲解Ting Zhang的Interleaved Group Convolutions for Deep Neural Networks,该文对Group convolution有较为详细的讲解。
Abstract
文章开篇引出了 IGCNets —— IGCNets 将两个个完整的卷积块打乱重组成一对连续的交错卷积,一个叫主卷积(primary group convolution),另一个叫从卷积(secondary group convolution),它们最主要的特点是:
(i) the convolution on each partition in primary group convolution is a spatial convolution, while on each partition in secondary group convolution, the convolution is a point-wise convolution; (ii) the channels in the same secondary partition come from different primary partitions.
- 在主群卷积内的所有卷积都是空间域卷积,而在第二组卷积(或者可以对应叫次群卷积)则是一个 point-wise 卷积,也就是 1$\times$1 卷积。
(ii) the channels in the same secondary partition come from different primary partitions.
- 次群卷积内的同一通道来自不同的主群卷积。
这是对于该网络独有结构的高度集中概括。
Introduction
这一部分首先讲到了一个许多模型都存在的问题——卷积核冗余(redundancy of convolutional kernels)。这一类冗余来自于两方面,第一方面是空域卷积,另一方面则是来自于多通道的问题。
the spatial extent, small kernels are developed, such as 3$\times 3 , 3 3, 3 3,3\times 1 , 1 1, 1 1,1\times$3. In the channel extent, group convolutions and channel-wise convolutions or separable filters, have been studied.
目前来看,空域冗余可以用小卷积核解决(small kernels),通道冗余则用通道可分离卷积来做,本文主要工作是后者。
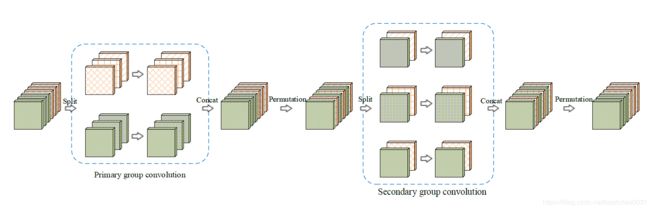
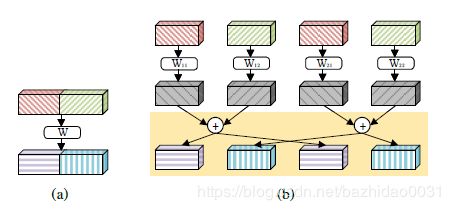
接下来就是介绍模型中最为重要的卷积交错组块(如下图):
主群卷积的输入来自于直接分割图像的通道,像上图有绿和黄两个主分区,每个主分区又依照通道有三个次分区,在主组卷积中,卷积完全是空域的,而次组卷积的1$\times$1卷积则是为了把主组卷积结果的不同通道混合。
原文中提到相同数量的参数/计算复杂度下,IGC块比常规的卷积的空间内核要大得多,换句话讲则是相同卷积核大小下,参数和计算复杂度小得多。并且,具有深刻意义的是:
It is known that a group convolution is equivalent to a regular convolution with sparse kernels: there is no connections across the channels in different partitions. Accordingly,
an IGC block is equivalent to a regular convolution with the kernel composed from the product of two sparse kernels, resulting in a dense kernel.
IGC块等价于由两个稀疏卷积核的乘积组成的常规卷积卷积,是一个密核,这一点在下面的文章里多次被提到,并进行了证明。
related work
这一节主要就组卷积与多分支结构、稀疏卷积核、张量分解三方面来描述了一下 IGCNets 的主要技术。
Group convolutions and multi-branch
Group convolution最初在AlexNet中提出,其初衷在于克服早期硬件计算资源不足的问题,将feature maps分到多张GPU上进行运算,有点类似于现在的分布式运算。
而 Multi-branch 则是
Our approach further improves parameter efficiency and adopts primary and secondary group convolutions, where secondary group convolution acts as a role of blending the channels outputted by primary group convolution.
文章在此处的重点就在于这最后一句,本模型的的对于原有模型的改进在于采用主次两级组卷积,其中次级组卷积用于混合不同通道输入。
Sparse convolutional kernels
稀疏卷积核部分,原文并没有讲的很详细,笔者结合自己查阅的知识来详细讲解(此节部分内容来自于网络)。

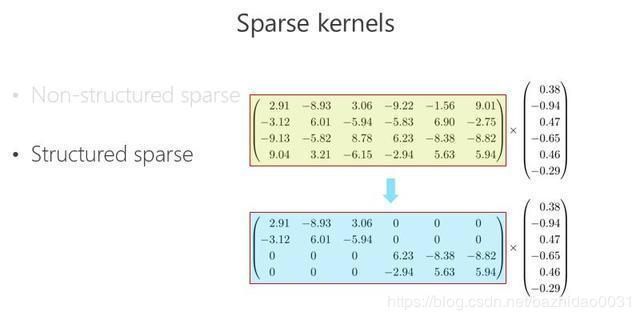
稀疏卷积核的本意也是想把矩阵跟向量相乘变得快一点、模型的参数少一点,于是有人想到了一种最简单的方法——把里面的有些数变成 0,比如 2.91 变成 0,3.06 变成 0,变成 0 以后就成了稀疏的矩阵,这个稀疏矩阵存储量会变小,如果你足够稀疏的话,计算量会小,因为直接是 0 就不用乘了。还有一种 Structured sparse(结构化稀疏),比如这种对角形式,矩阵跟向量相乘,可以优化得很好。正如下图所示,这里 Structured sparse 就是本文组卷积(Group convolution)所用到的。
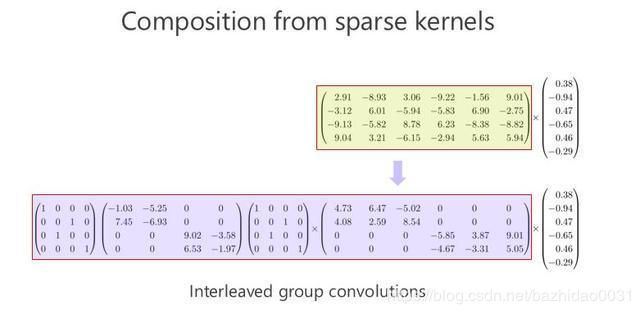
这也就是文章中多次提到的一句话:一个密矩阵可以由过多个稀疏矩阵相乘来近似。
Decomposition
对于张量分解,可以理解为矩阵分解向多维的延伸,也可以理解为对高维数据的一种低秩逼近或者特征提取,可以减少冗余和加速运算,除了文章中的方法,主要有 CP 分解和 Tucker 分解两种。
Rather than compressing previouslytrained networks by approximating a convolution kernel using the product of two sparse kernels corresponding to our primary and secondary group convolutions, we train our network from scratch and show that our network can improve parameter efficiency and classification accuracy.
本节最后也提到本文不是通过用两个稀疏的内核来近似一个卷积核来压缩以前训练过的网络,而是用我们的主次和次组卷积来计算我们的网络,并证明我们的网络可以提高参数效率和分类精度。
Our Network
Interleaved Group Convolutions
Definition
在这里,文章又一次提到了 IGC 块与稀疏卷积核的关系,说明这一点很重要,因此笔者将此处原文贴出:
A group convolution can be viewed as a regular convolution with a sparse block-diagonal convolution kernel, where each block corresponds to a partition of channels and there are no connections across the partitions.
最后一段提到的比较重要的的信息是原文作者建议主级组卷积采用 3$\times 3 的 卷 积 核 , 而 次 级 组 卷 积 为 了 混 合 输 入 的 图 像 的 通 道 自 然 只 能 选 择 1 3 的卷积核,而次级组卷积为了混合输入的图像的通道自然只能选择 1 3的卷积核,而次级组卷积为了混合输入的图像的通道自然只能选择1\times$1 卷积核。
Primary group convolutions
在讲这部分内容之前,我们先明确几组参数的意义。
- L 代表分区数。
- M 代表通道数。
- S 代表卷积核尺寸,比如 3$\times$3 卷积核的尺寸 S 就是9。
- Z L是 (M S) 维向量。
- Wpll是一个 M × \times ×(M S)大小类的矩阵。
下面就是主级组卷积的数学表达式:
其中,x = [ ZT1 ZT2 … ZTL ]T 就是整个模型在各个分区各个通道的输入;Wpll 是对应第 L 分区的卷积核。
把上式展开就可以看出来该式的含义无非是对每一分区的图做不同的映射处理:
Secondary group convolutions
根据上面我们提到的理论,我们可以清楚的直到文章作者在次组卷积所采用的策略:次组卷积的第 m 个分区来自于主组卷积的第 m 个输出通道。
P 在这里就是负责把输入的多个矩阵重新排列的矩阵。
而第m个次组卷积分区的操作就是:
![]()
Wdmm是对应于第m个次组卷积分区的 1 × 1 1\times1 1×1 卷积核,其本身是一个大小为 L × L L \times L L×L 的矩阵。次组卷积的输出结果需要作为下一个 IGC 块的输入,因此必然会经历一个与主组卷积之后镜像的过程,以达到使次组卷积输出回到原有输出的形式:
这里因为原文描述比较详细,就没有过多重复,其实笔者觉得这里的过程结合上面的 IGC 结构图来看很清楚明白。
(这里的部分原文中没有,是笔者结合自己查阅的内容对最后一个式子进行补充描述。)
最后一个式子按原文作者话讲是为了引进一个严格的互补条件:如果有两个通道在第一组卷积里面,落在同一个Branch(分支),就希望在第二组里面落在不同的Branch(分支)。第二组里面比如一个Branch(分支)里面的若干个通道,要来自于第一个组卷积里面的所有Branches(分支),这个称为互补条件。这个互补条件会带来什么?它会带来(任何一对输入输出通道之间存在)path,也就是说相乘矩阵是密集矩阵。并且重要的是,任何一个 input 和 output 之间有一条path,而且有且只有一条path。
好处显而易见是模型变宽,坏处就是模型在这个地方可能会过于稀疏,反而导致整体不会达到一个最优的效果。
Analysis
Wider than regular convolutions
考虑到次组卷积的卷积核大小是 1 × \times × 1,那么整个 IGC 块的参数量是:
其中,G = ML 就是这节重点要讨论的 IGC 块的宽度。
对于大小为S卷积核的普通卷积而言,如果输入与输出的宽度是C,那么参数量就是:Tigc=Trc=T ,则我们得到:
C 2 = T / S C^2=T/S C2=T/S, G 2 = 1 S L + 1 M T G^2=\dfrac{1}{\tfrac{S}{L}+\tfrac{1}{M}}T G2=LS+M11T
顺势可以推得:
考虑到主组卷积的核大小 3 × 3 3\times3 3×3,我们可以得出当 L > 1 L>1 L>1时, G > C G>C G>C。也就是说除了 L = 1 L=1 L=1这种特殊情况,IGC 块都要比普通卷积组要宽。
When is the widest?
这节主要讨论主次组卷积的 L 和 M 参数如何来影响最终的 IGC 块宽度。从 IGC 块参数量的公式我们可以推得:
这个式子第三行的不等式意味着宽度 G 是有上限的:
当 L = M S L=MS L=MS 时,宽度是最好的。
Wider leads to better performance?
前面说到了一个 IGC块等于一个由两个稀疏卷积组成的普通卷积: W = P W d P T W p W=PW^dP^TW^p W=PWdPTWp ,也就是说从参数角度来讲有下面的约束:
∣ ∣ W P ∣ ∣ 0 + ∣ ∣ W d ∣ ∣ 0 = T ||W^P||_0+||W^d||_0=T ∣∣WP∣∣0+∣∣Wd∣∣0=T
( ∣ ∣ ⋅ ∣ ∣ 0 ||·||_0 ∣∣⋅∣∣0 是矩阵的 l 0 l_0 l0 范数)
This equation means that when the IGC is wider (or the dimension of the input x is higher), Wp and Wd are larger but more sparse.
IGC 块越宽,主次组卷积的一二级卷积矩阵越稀疏。这样也就是说,并非 IGC 块的宽度越宽,性能就更好,这是一个权衡的过程。
Discussions and Connections
这一章节主要讨论 IGC 块与普通组卷积、ResNet 和 Xception 结构的联系。
Connection to regular convolutions
对于普通组卷积而言,空域上单个点的映射过程是 X`=Wx。IGC 块以 L = 4 L=4 L=4 举例而言(就像最开始的结构图那样):
W p W^p Wp是块对角矩阵:
W p = d i a g ( W 11 , W 12 , W 21 , W 22 ) W^p=diag(W_{11},W_{12},W_{21},W_{22}) Wp=diag(W11,W12,W21,W22)
W i j W_{ij} Wij是 W 的 2 × 2 2\times2 2×2分块矩阵。
W = [ W 11 W 12 W 21 W 22 ] W=\begin{bmatrix}{W_{11}}&{W_{12}}\\{W_{21}}&{W_{22}}\\\end{bmatrix} W=[W11W21W12W22]
W d W^d Wd 也是一个块对角矩阵,只不过它的大小是 L × L L \times L L×L,并且所有的 W d W^d Wd 都是一样的:
W 11 d = W 22 d = ⋯ = W M M d = [ 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 ] W^d_{11}=W^d_{22}=\cdots=W^d_{MM}=\begin{bmatrix} {1}&{1}&{0}&{0}\\ {0}&{0}&{1}&{1}\\ {1}&{1}&{0}&{0}\\ {0}&{0}&{1}&{1}\\ \end{bmatrix} W11d=W22d=⋯=WMMd=⎣⎢⎢⎡1010101001010101⎦⎥⎥⎤
附注: 从这里, W d W^d Wd 和 W p W^p Wp 的结构和量值我们就可以清楚地印证上文所讲的内容—— W p W^p Wp 是主组卷积中的同分区内卷积过程,而 W d W^d Wd 是次组卷积中为了混合不同通道的卷积过程。
Connection to summation fusion
(a图是普通组卷积,b图是summation fusion)
summation fusion 的代表性结构是 ResNet ,其重要的操作是求和接收所有的输入,并将它们加在一起作为多个输出:
这个用交叉组卷积的形式来表示的话, W m m d W^d_{mm} Wmmd 就是一个全1卷积核。在有4个主分区的情况下:
W 11 d = W 22 d = ⋯ = W M M d = [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ] W^d_{11}=W^d_{22}=\cdots=W^d_{MM}=\begin{bmatrix}{1}&{1}&{1}&{1}\\{1}&{1}&{1}&{1}\\{1}&{1}&{1}&{1}\\ {1}&{1}&{1}&{1}\\ \end{bmatrix} W11d=W22d=⋯=WMMd=⎣⎢⎢⎡1111111111111111⎦⎥⎥⎤
Xception is an extreme case
这一节我们讨论两个极端情况:L=1 和 M=1。
在L=1的情况下,主组卷积变成了一个常规的卷积,而次组卷积的行为就像分配不同权重(weight)的每个通道。
在M=1的情况下,主组卷积变成了一个极端的组卷积:一个 channel-wise 组卷积,而第二组卷积变成了一个 1 × 1 1\times1 1×1的卷积。
这两个极端情况很接近于 Xception —— 在一个 channel-wise 空间卷积前放置一个 1 × 1 1\times1 1×1 卷积。而在 Xception: Deep learning with depthwise separable convolutions. 一文中指出 1 × 1 1\times1 1×1 卷积放置在 channel-wise 空间卷积前后都没有影响。
而原文中的这张表也显示出这两种极端情况都不是最优结果,换句话而言,Xception 作为 IGCNets 的极端情况是不如 IGCNets 本身的。
Extensions and variants
三点补充:
- 主组卷积和次组卷积并不是固定的,二者之间可以交换位置。
- 次组卷积可以用线性映射或者普通空间卷积代替,只要其可以完成通道分配任务。但是原文中没有提到,因为考虑到额外的参数和计算复杂度的原因。
- 文章中介绍的 IGC 块可以作为现有模型的补充。比如其他模型采用的 1 × 3 1\times3 1×3 和 3 × 1 3\times1 3×1 卷积也可以用到主组卷积中。
GITHUB:https://blog.csdn.net/bazhidao0031/article/details/81937653(非笔者所写,后面有空再补)