神经网络梯度下降优化算法及初始化方法小结

An overview of gradient descent optimization algorithms and Weight initialization methods.

神经网络重要的一点就是调参炼丹，这里复习一下网络的初始化方法及优化方法。
然而知道这些并没有什么用， 平时多实验才是王道

1 网络优化方法

这里主要说明一些关于梯度下降的方法，梯度下降顾名思义就是按照梯度来更新参数

优化方法有很多，caffe中支持下面几种：

• SGD stochastic gradient descent
• AdaDelta
• Adam
• Nesterov
• RMSProp

这里我们会结合其他课程或者博客比如 cs231n或者 https://arxiv.org/pdf/1609.04747.pdf

1.1 SGD

梯度下降的方法有很多
其中用全部数据来进行梯度下降的称为Batch Gradient Descent，这种方法的缺点是更新慢而且内存需求大
其优化方式可以看为：

params = params - learning_rate * params_grad

显然上面的数据使用方法不适合大数据的使用，于是可以每次只取一个或者一部分样本进行训练，现在我们常用是Mini Batch Gradient Descent 但是下文仍然称为SGD，SGD有些时候是用来描述每次只取一个样本的方法，Mini Batch Gradient Descent 比起每次随机取一个样本的方法 训练波动更小，更加稳定，更加高效，这基本上是最常用的一种优化方法，虽然没有很多技巧但是比较稳定

1.2 Momentum

其更新公式如下：

vt=γvt−1+η∇θJ(θ)

θ=θ−vt

sgd的公式可以看为

θ=θ−η∇θJ(θ)

可以看出momentum考虑了之前一次更新，如果每次更新方向一致，那么其更新的速度会越来越快，如果方向改变，则会降低更新速度，eta可以看成摩擦因子一样的因子，相比sgd，理论上momentum可以减少动荡，加快收敛

1.3 Nesterov

Nesterov 认为我们更新的时候应该考虑前面的位置

θ2=θ−γvt−1

vt=γvt−1+η∇θJ(θ2)

θ=θ−vt

与moment的区别可以视为：

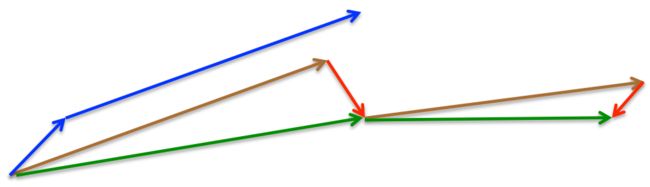
momentum首先计算一个梯度(短的蓝色向量)，然后在加速更新梯度的方向进行一个大的跳跃(长的蓝色向量)，nesterov项首先在之前加速的梯度方向进行一个大的跳跃(棕色向量)，计算梯度然后进行校正(绿色梯向量)

1.4 Adagrad

之前每次更新所有参数的学习率都是一样的，Adagrad是用不同的学习率更新不同的参数

gt,i=∇θJ(θi)

θt+1,i=θt,i−ηGt,ii+ϵ−−−−−−−√⋅gt,i

\epsilon 常取1e-8等数用来避免分母为0
G_t 是一个对角矩阵，对应\theta_i梯度的平方和
可以看出式中分母是不断增加的，随着梯度的增多学习率逐渐减少

1.5 Adadelta

adadelta将adagred分母中的平方累加替换为了权重均值

θt+1=θt+Δθt

Δθt=−ηE[g2]t+ϵ−−−−−−−−√gt

E[g2]t=γE[g2]t−1+(1−γ)g2t

这样一来分母中累计项离当前时间点比较近的项，同时论文中利用近似的牛顿法生成了下式，不在需要手动设置eta：

θt+1=θt+Δθt

Δθt=−E[Δθ2]t−1−−−−−−−−√E[g2]t+ϵ−−−−−−−−√gt

E[Δθ2]t=γE[Δθ2]t−1+(1−γ)Δθ2t

E[g2]t=γE[g2]t−1+(1−γ)g2t

1.6 RMSprop

RMSprop 出自 Geoff Hinton的课件

http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf

可以看成是adadelta的特例

E[g2]t=0.9E[g2]t−1+0.1g2t

θt+1=θt−ηE[g2]t+ϵ−−−−−−−−√gt

1.7 Adam

前面是对于每个参数的学习率的自适应调整，这里添加了对于每个参数的动量自适应调整

mt=β1mt−1+(1−β1)gt

vt=β2vt−1+(1−β2)g2t

m^t=mt1−βt1

v^t=vt1−βt2

θt+1=θt−ηv^t−−√+ϵm^t

注m_t对应均值 v_t对应偏心方差 β1 and β2 are close to 1

1.8 AdaMax

此处将adam中的v_t泛化了：

vt=βp2vt−1+(1−βp2)|gt|p

Kingma and Ba发现p取正无穷的时候，效果不错
于是

ut=β∞2vt−1+(1−β∞2)|gt|∞

=max(β2⋅vt−1,|gt|)

θt+1=θt−ηutm^t

1.9 Nadam

Nadam (Nesterov-accelerated Adaptive Moment Estimation)= Adam + NAG（ Nesterov accelerated gradient）

nag：

gt=∇θtJ(θt−γmt−1)

mt=γmt−1+ηgt

θt+1=θt−mt

modify nag

gt=∇θtJ(θt)

mt=γmt−1+ηgt

θt+1=θt−(γmt+ηgt)

“`

adam 引入nag：

mt=β1mt−1+(1−β1)gt

m^t=mt1−βt1

θt+1=θt−ηv^t−−√+ϵm^t

2 网络初始化方法

网络初始化
1. 首先应该要注意不能全部初始为相同的值
2. 其次不可以太大，太大易对输入更敏感或者容易在梯度反向传播引起大的波动

这里摘取DeepLearning中文版中的一段话

我们几乎总是初始化模型的权重为高斯或均匀分布中随机抽取的值。高斯或均
匀分布的选择似乎不会有很大的差别，但也没有被详尽地研究。然而，初始分布的
大小确实对优化过程的结果和网络泛化能力都有很大的影响

随着bn等新的层的提出对于初始化的方法现在网络有更强的容忍度了，不过还是有影响的

主要介绍几种常用的初始化方法

• Gaussian
• uniform
• Xavier
• MSRA

除此之外也有很多对于初始化的探索，比如将权重初始化为正交矩阵等等

https://keras-cn.readthedocs.io/en/latest/other/initializations/

2.1 高斯

高斯初始化给定均值与标准差 比如均值一般为0，标准差为 0.01 或0.001

2.2 uniform

取均匀分布的数值比如从0到1之间随机取 Xavier也是属于均匀分布的一种

2.3 Xavier

为了保证前传和反传过程中不会遇到输出方差越来越大或者越来越小的情况，将其初始化为均匀分布：

U(-sqrt(6/(m+n)),sqrt(6/(m+n)))

上式中n为输入神经元个数，m为输出神经元的个数
默认的时候
这部分冯超同学已经写的很好了，愿意看公式推导的请移步：
https://zhuanlan.zhihu.com/p/22028079

caffe默认只考虑输入个数，即控制前传

2.4 MSRA

https://arxiv.org/pdf/1502.01852.pdf

推导思路与xariver，只不过针对ReLU和PReLU做了了特殊的计算，只考虑前传时 ReLU对应的初始化为均值为0 标准差为sqrt(2/n)的高斯分布
并且可以认为靠考虑前传或者反传得到的初始化模型都可以保证网络在两个过程输出的结果不会大或者太小。
PReLU时要做相应的改变：

mean=0
std=sqrt(2/(1+a**2))
a是小于时的斜率

偷来一些干货

https://zhuanlan.zhihu.com/p/22028079
1. sigmoid在压缩数据幅度方面有优势，对于深度网络，使用sigmoid可以保证数据幅度不会有问题，这样数据幅度稳住了就不会出现太大的失误。
2. 但是sigmoid存在梯度消失的问题，在反向传播上有劣势，所以在优化的过程中存在不足
3. relu不会对数据做幅度压缩，所以如果数据的幅度不断扩张，那么模型的层数越深，幅度的扩张也会越厉害，最终会影响模型的表现。
4. 但是relu在反向传导方面可以很好地将“原汁原味”的梯度传到后面，这样在学习的过程中可以更好地发挥出来。（这个“原汁原味”只可意会，不必深究）这么来看，sigmoid前向更靠谱，relu后向更强。