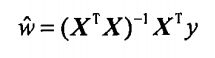LinearRegression
线性回归
f(x) = wx + b
这个函数的导数就是3, 斜率 代表增长率
import numpy as np
import matplotlib.pyplot as pltx = np.linspace(0, 3 * np.pi, 100)
# 正弦函数
y = np.sin(x)
plt.plot(x, y)
# 余弦
y_daoshu = np.cos(x)
plt.plot(x, y_daoshu, c='green')[]
【关键词】最小二乘法,线性
一、普通线性回归
import numpy as np#原矩阵
x = np.array([[1,2,3],[4,5,6]])
x输出
array([[1, 2, 3],
[4, 5, 6]])
#要求矩阵的逆,满秩矩阵才有 逆矩阵
#3x3的方阵 * 3x3.T = 3x3#x不是反正
#np.linalg.inv(x)#(原矩阵 * 矩阵的转置矩阵 )
#x现在的x不满足方阵的条件
#让x * X.T,变为方阵
XT = x.T
XT输出
array([[1, 4],
[2, 5],
[3, 6]])
#转变为方阵了
xXT = np.dot(x,XT)
xXT输出
array([[14, 32],
[32, 77]])
#求矩阵的逆
#方阵* 方阵的逆 = 单位矩阵
inv_ = np.linalg.inv(xXT)
inv_输出
array([[ 1.42592593, -0.59259259],
[-0.59259259, 0.25925926]])
eye_ = np.dot(inv_,xXT)
eye_输出
array([[1., 0.],
[0., 1.]])
np.dot(eye_,x)输出
array([[1., 2., 3.],
[4., 5., 6.]])
np.dot(xXT,eye_)输出
array([[14., 32.],
[32., 77.]])
np.dot(eye_,xXT)输出
array([[14., 32.],
[32., 77.]])
#( y-x*w)**2
#x是个矩阵,y当做常数
#求导
(y - x*w) ** 2 = 0
#求导的初步公式
2 * (y - x * w) * (0 - x * 1 * 1 ) = 0
#化简
#1.
2 * (y - x * w) * (- x ) = 0
#2.同除2
(y - x * w) * (- x ) = 0
#3.同乘以-1
(y - x * w) * x = 0
#4.两边同乘以 x 的转置矩阵, 记为 XT
(y - x * w) * (x * XT) = 0
#5.两边同乘以 (x * XT) 的逆矩阵 ,逆矩阵记为 INV
y - x * w= 0
#6.
x * w = y
#7.x是一个矩阵,就逆,转为单位矩阵
x * XT * w = XT * y
#8.乘以x * XT 的逆
(x * XT) * INV * w = INV * XT * y
#解开
w^ = (x * XT)^-1 * XT *y1、原理
分类的目标变量是标称型数据,而回归将会对连续型的数据做出预测。
应当怎样从一大堆数据里求出回归方程呢?
假定输人数据存放在矩阵X中,而回归系数存放在向量W中。那么对于给定的数据X1, 预测结果将会通过
Y=X*W
给出。现在的问题是,手里有一些X和对应的Y,怎样才能找到W呢?
一个常用的方法就是找出使误差最小的W。这里的误差是指预测Y值和真实Y值之间的差值,使用该误差的简单累加将使得正差值和负差值相互抵消,所以我
们采用平方误差。
最小二乘法
平方误差可以写做:
对W求导,当导数为零时,平方误差最小,此时W等于:
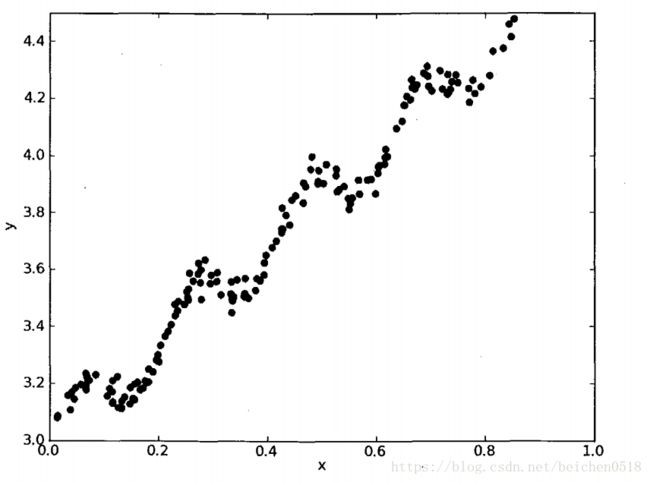
例如有下面一张图片:
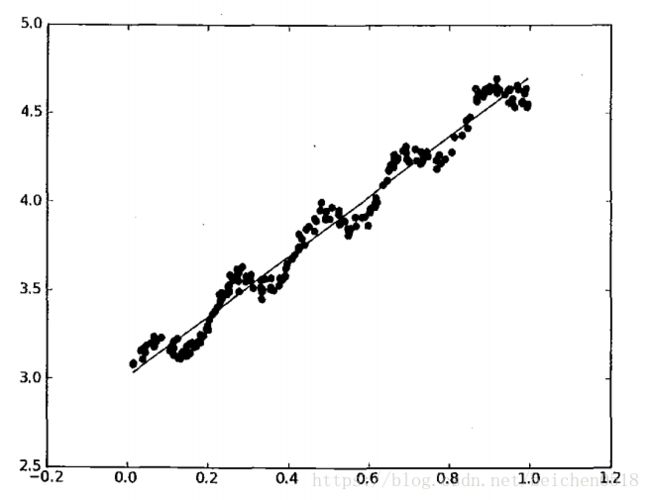
求回归曲线,得到:
2、实例
不那么准确
使用线性回归分析糖尿病数据
from sklearn.linear_model import LinearRegression
import sklearn.datasets as datasets# 获取数据
diabetes = datasets.load_diabetes()
diabetes输出
{‘DESCR’: ‘Diabetes dataset\n================\n\nNotes\n—–\n\nTen baseline variables, age, sex, body mass index, average blood\npressure, and six blood serum measurements were obtained for each of n =\n442 diabetes patients, as well as the response of interest, a\nquantitative measure of disease progression one year after baseline.\n\nData Set Characteristics:\n\n :Number of Instances: 442\n\n :Number of Attributes: First 10 columns are numeric predictive values\n\n :Target: Column 11 is a quantitative measure of disease progression one year after baseline\n\n :Attributes:\n :Age:\n :Sex:\n :Body mass index:\n :Average blood pressure:\n :S1:\n :S2:\n :S3:\n :S4:\n :S5:\n :S6:\n\nNote: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times
n_samples(i.e. the sum of squares of each column totals 1).\n\nSource URL:\nhttp://www4.stat.ncsu.edu/~boos/var.select/diabetes.html\n\nFor more information see:\nBradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) “Least Angle Regression,” Annals of Statistics (with discussion), 407-499.\n(http://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)\n’,
‘data’: array([[ 0.03807591, 0.05068012, 0.06169621, …, -0.00259226,
0.01990842, -0.01764613],
[-0.00188202, -0.04464164, -0.05147406, …, -0.03949338,
-0.06832974, -0.09220405],
[ 0.08529891, 0.05068012, 0.04445121, …, -0.00259226,
0.00286377, -0.02593034],
…,
[ 0.04170844, 0.05068012, -0.01590626, …, -0.01107952,
-0.04687948, 0.01549073],
[-0.04547248, -0.04464164, 0.03906215, …, 0.02655962,
0.04452837, -0.02593034],
[-0.04547248, -0.04464164, -0.0730303 , …, -0.03949338,
-0.00421986, 0.00306441]]),
‘feature_names’: [‘age’,
‘sex’,
‘bmi’,
‘bp’,
‘s1’,
‘s2’,
‘s3’,
‘s4’,
‘s5’,
‘s6’],
‘target’: array([151., 75., 141., 206., 135., 97., 138., 63., 110., 310., 101.,
69., 179., 185., 118., 171., 166., 144., 97., 168., 68., 49.,
68., 245., 184., 202., 137., 85., 131., 283., 129., 59., 341.,
87., 65., 102., 265., 276., 252., 90., 100., 55., 61., 92.,
259., 53., 190., 142., 75., 142., 155., 225., 59., 104., 182.,
128., 52., 37., 170., 170., 61., 144., 52., 128., 71., 163.,
150., 97., 160., 178., 48., 270., 202., 111., 85., 42., 170.,
200., 252., 113., 143., 51., 52., 210., 65., 141., 55., 134.,
42., 111., 98., 164., 48., 96., 90., 162., 150., 279., 92.,
83., 128., 102., 302., 198., 95., 53., 134., 144., 232., 81.,
104., 59., 246., 297., 258., 229., 275., 281., 179., 200., 200.,
173., 180., 84., 121., 161., 99., 109., 115., 268., 274., 158.,
107., 83., 103., 272., 85., 280., 336., 281., 118., 317., 235.,
60., 174., 259., 178., 128., 96., 126., 288., 88., 292., 71.,
197., 186., 25., 84., 96., 195., 53., 217., 172., 131., 214.,
59., 70., 220., 268., 152., 47., 74., 295., 101., 151., 127.,
237., 225., 81., 151., 107., 64., 138., 185., 265., 101., 137.,
143., 141., 79., 292., 178., 91., 116., 86., 122., 72., 129.,
142., 90., 158., 39., 196., 222., 277., 99., 196., 202., 155.,
77., 191., 70., 73., 49., 65., 263., 248., 296., 214., 185.,
78., 93., 252., 150., 77., 208., 77., 108., 160., 53., 220.,
154., 259., 90., 246., 124., 67., 72., 257., 262., 275., 177.,
71., 47., 187., 125., 78., 51., 258., 215., 303., 243., 91.,
150., 310., 153., 346., 63., 89., 50., 39., 103., 308., 116.,
145., 74., 45., 115., 264., 87., 202., 127., 182., 241., 66.,
94., 283., 64., 102., 200., 265., 94., 230., 181., 156., 233.,
60., 219., 80., 68., 332., 248., 84., 200., 55., 85., 89.,
31., 129., 83., 275., 65., 198., 236., 253., 124., 44., 172.,
114., 142., 109., 180., 144., 163., 147., 97., 220., 190., 109.,
191., 122., 230., 242., 248., 249., 192., 131., 237., 78., 135.,
244., 199., 270., 164., 72., 96., 306., 91., 214., 95., 216.,
263., 178., 113., 200., 139., 139., 88., 148., 88., 243., 71.,
77., 109., 272., 60., 54., 221., 90., 311., 281., 182., 321.,
58., 262., 206., 233., 242., 123., 167., 63., 197., 71., 168.,
140., 217., 121., 235., 245., 40., 52., 104., 132., 88., 69.,
219., 72., 201., 110., 51., 277., 63., 118., 69., 273., 258.,
43., 198., 242., 232., 175., 93., 168., 275., 293., 281., 72.,
140., 189., 181., 209., 136., 261., 113., 131., 174., 257., 55.,
84., 42., 146., 212., 233., 91., 111., 152., 120., 67., 310.,
94., 183., 66., 173., 72., 49., 64., 48., 178., 104., 132.,
220., 57.])}
"""
'age', 年龄
'sex', 性别
'bmi', 体重指数
'bp', 血压
's1', 血清
's2',
's3',
's4',
's5',
's6'
"""
data = diabetes['data']
target = diabetes['target']
# 年龄越大,几率越高
data.shape输出
(442, 10)
抽取训练数据和预测数据
# 选择2个条件作为预测的数据
data_part = data[:, [0, 2]]
# 实例化
lrg = LinearRegression()# 对数据进行训练
# 训练一组数据
lrg.fit(data[:,[0]], target)输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
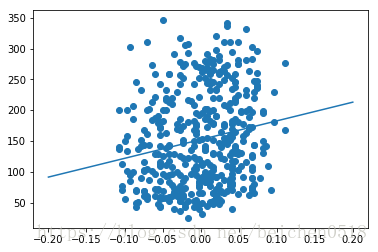
#散点图
plt.scatter(data[:,[0]], target)
创建数学模型
# 预测数据
X_test = np.linspace(-0.2, 0.2, 1000).reshape(1000,1)
y_ = lrg.predict(X_test)
plt.scatter(data[:,[0]], target)
plt.plot(X_test, y_)[]
lrg.fit(data, target)- 输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# 回归求的是系数
# 10个属性, 442个样本就是442个方程, 10w
lrg.coef_输出
array([ -10.01219782, -239.81908937, 519.83978679, 324.39042769,
-792.18416163, 476.74583782, 101.04457032, 177.06417623,
751.27932109, 67.62538639])
lrg.score(data, target)输出
0.5177494254132934
斜率,截距
# 线性回归的数据
x = np.arange(0, 10).reshape((10,1))
y = 3 * x + 15
lrg = LinearRegression()
lrg.fit(x, y)输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# 斜率
lrg.coef_输出
array([[3.]])
# 截距
lrg.intercept_输出
array([15.])
更复杂
x1 = np.arange(0, 10).reshape((10, 1))
x2 = np.random.randint(0, 30, size=(10, 1))
y = 3 * x1 + 5 * x2 + 15
lrg = LinearRegression()
# np.c_[]
X_train = np.c_[x1, x2]
X_train输出
array([[ 0, 22],
[ 1, 13],
[ 2, 27],
[ 3, 26],
[ 4, 27],
[ 5, 28],
[ 6, 22],
[ 7, 9],
[ 8, 19],
[ 9, 17]])
lrg.fit(X_train,y)输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
lrg.coef_输出
array([[3., 5.]])
lrg.intercept_输出
array([15.])
5个属性
x = np.random.randint(0, 50 , size=(10, 5))
# 系数
w = np.random.randint(0,10, size=5)
y = np.dot(x, w)display(x, w, y)输出
array([[14, 25, 23, 14, 22],
[12, 19, 46, 10, 16],
[19, 5, 6, 15, 9],
[17, 6, 18, 40, 13],
[41, 44, 19, 13, 17],
[10, 0, 30, 6, 13],
[42, 46, 39, 21, 49],
[38, 15, 7, 31, 14],
[24, 25, 37, 34, 11],
[18, 27, 20, 43, 32]])array([3, 5, 0, 3, 7])
array([363, 273, 190, 292, 501, 139, 762, 380, 376, 542])
lrg = LinearRegression()
lrg.fit(x, y)输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
lrg.coef_输出
array([ 3.00000000e+00, 5.00000000e+00, -2.22044605e-15, 3.00000000e+00,
7.00000000e+00])
lrg.intercept_输出
1.7053025658242404e-13
二、岭回归
岭回归
x输出
array([[1, 2, 3],
[4, 5, 6]])
#x的转置矩阵
X_T = x.T
X_T输出
array([[1, 4],
[2, 5],
[3, 6]])
#转置矩阵 * 原矩阵
XTx = np.dot(X_T,x)
XTx输出
array([[17, 22, 27],
[22, 29, 36],
[27, 36, 45]])
#加入惩罚项 入 lambda
lam = 0.00001
_eye = np.eye(3)
lam_eye=np.dot(lam,_eye)
lam_eye输出
array([[1.e-05, 0.e+00, 0.e+00],
[0.e+00, 1.e-05, 0.e+00],
[0.e+00, 0.e+00, 1.e-05]])
#加上惩罚项目
XTx_ = XTx + lam_eye
XTx_输出
array([[17.00001, 22. , 27. ],
[22. , 29.00001, 36. ],
[27. , 36. , 45.00001]])
#对加入惩罚项的方阵求逆
_inv = np.linalg.inv(XTx_)
_inv
# 奇异矩阵->非满秩:非满秩矩阵是不能逆的输出
array([[ 16667.75615415, -33333.17901392, 16665.88581511],
[-33333.17901392, 66666.69135574, -33333.43826881],
[ 16665.88581511, -33333.43826881, 16667.23764437]])
b = np.dot(_inv,XTx_)
b输出
array([[ 1.00000000e+00, 1.89174898e-10, 2.53936434e-10],
[-1.01863407e-10, 1.00000000e+00, -6.85794835e-11],
[ 6.91215973e-11, 1.45519152e-11, 1.00000000e+00]])
np.dot(x,b)输出
array([[1., 2., 3.],
[4., 5., 6.]])
x输出
array([[1, 2, 3],
[4, 5, 6]])
# 引入岭回归的包
from sklearn.linear_model import Ridgex = np.random.randint(0, 10, size=(2, 2))
w = np.array([1, 2])
y = np.dot(x, w)
display(x, w, y)输出
array([[0, 9],
[2, 1]])array([1, 2])
array([18, 4])
1、原理
缩减系数来“理解”数据
如果数据的特征比样本点还多应该怎么办?是否还可以使用线性回归和之前的方法来做预测?
答案是否定的,即不能再使用前面介绍的方法。这是因为输入数据的矩阵X不是满秩矩阵。非满秩矩阵在求逆时会出现问题。
为了解决这个问题,统计学家引入了岭回归(ridge regression)的概念
# 特征 = 属性(未知数), 样本 = 方程
# 未知数 > 方程 : 这个题无解
x = np.random.randint(0, 20, size=(10, 15))
w = np.random.randint(0, 15, size=15)
y = np.dot(x, w)
display(x, w, y)输出
array([[ 5, 3, 3, 11, 5, 19, 17, 17, 4, 7, 13, 13, 16, 2, 8],
[14, 15, 12, 18, 12, 19, 17, 12, 5, 18, 2, 8, 14, 5, 0],
[ 4, 5, 15, 0, 3, 17, 14, 15, 8, 4, 7, 0, 1, 5, 16],
[18, 3, 8, 13, 4, 11, 13, 1, 3, 18, 8, 19, 11, 7, 4],
[ 0, 14, 10, 16, 16, 12, 16, 14, 15, 14, 5, 6, 3, 5, 14],
[13, 7, 1, 19, 18, 4, 8, 2, 14, 4, 18, 11, 10, 16, 3],
[ 3, 6, 11, 19, 5, 14, 17, 6, 3, 14, 5, 10, 19, 12, 13],
[14, 16, 5, 15, 12, 17, 0, 8, 5, 1, 17, 6, 10, 3, 14],
[11, 1, 18, 6, 13, 9, 19, 15, 2, 11, 9, 19, 19, 11, 6],
[ 8, 0, 15, 2, 5, 2, 7, 16, 4, 13, 17, 6, 3, 2, 5]])array([13, 14, 13, 7, 7, 13, 9, 7, 11, 1, 11, 1, 13, 13, 8])
array([1282, 1592, 1165, 1190, 1404, 1406, 1430, 1467, 1506, 904])
# 先用线性回归
lrg = LinearRegression()
lrg.fit(x, y)输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
lrg.coef_输出
array([ 17.27327749, 7.72251335, -9.07052537, -8.58340761,
18.58514717, -0.93375352, 1.60685402, 5.59240136,
8.93420804, 3.47956082, -13.95656433, -11.3409328 ,
28.61977273, 4.10839164, 13.88337218])
满秩矩阵
# np帮我们识别是不是一个满秩矩阵
nd = np.array([[1, 2],[2, 3]])
nd输出
array([[1, 2],
[2, 3]])
# matrix_rank 求出来的是秩
np.linalg.matrix_rank(nd)输出
2
奇异矩阵
nd1 = np.array([[1, 2],[2, 4]])矩阵求逆
AB = BA岭回归计算
x = np.random.randint(0, 20, size=(10, 15))
w = np.random.randint(0, 15, size=15)
y = np.dot(x, w)
display(x, w, y)输出
array([[ 1, 11, 3, 14, 16, 19, 13, 5, 7, 15, 1, 4, 13, 5, 19],
[ 2, 11, 14, 9, 7, 0, 15, 16, 17, 10, 19, 2, 14, 14, 17],
[ 1, 1, 9, 12, 11, 4, 8, 14, 12, 19, 17, 8, 17, 19, 2],
[12, 14, 2, 13, 2, 18, 10, 18, 2, 11, 8, 0, 6, 19, 10],
[17, 16, 1, 7, 17, 11, 13, 10, 15, 14, 17, 11, 16, 6, 12],
[ 8, 14, 12, 6, 0, 17, 17, 12, 7, 6, 15, 9, 7, 6, 0],
[ 5, 2, 16, 17, 18, 1, 7, 17, 8, 1, 3, 11, 3, 4, 14],
[19, 6, 10, 11, 13, 10, 8, 9, 9, 11, 8, 3, 6, 0, 11],
[ 7, 10, 18, 8, 5, 8, 15, 8, 9, 2, 7, 9, 8, 13, 17],
[ 5, 6, 10, 6, 15, 17, 12, 13, 18, 11, 11, 5, 8, 8, 2]])array([ 1, 7, 8, 6, 12, 10, 1, 4, 0, 7, 11, 1, 13, 14, 8])
array([1112, 1203, 1219, 1079, 1230, 864, 808, 841, 978, 1012])
np.linalg.matrix_rank(x)输出
10
缩减方法可以去掉不重要的参数,因此能更好地理解数据。此外,与简单的线性回归相比,缩减法能取得更好的预测效果。
岭回归是加了二阶正则项(单位矩阵)的最小二乘,主要适用于过拟合严重或各变量之间存在多重共线性的时候,岭回归是有bias的,这里的bias是为了让variance更小。
# alpha 代表lambda
ridge = Ridge(alpha=0.001, fit_intercept=False)
ridge.fit(x, y)输出
Ridge(alpha=0.001, copy_X=True, fit_intercept=False, max_iter=None,
normalize=False, random_state=None, solver=’auto’, tol=0.001)
ridge.coef_输出
array([ 2.367746 , 4.37173185, 4.14640671, 7.70974142, 6.76429806,
7.32726997, 6.74328557, 5.59257023, 5.43193281, 10.73855648,
5.71339423, 4.59714618, 10.47201182, 13.11569657, 8.06191868])
绘制岭迹线
# 绘制岭迹线 ,选取最优值
x = 1 / (np.arange(0,10) + np.arange(1, 11).reshape((10,1)))
y = np.ones(10)
display(x, y)输出
array([[1. , 0.5 , 0.33333333, 0.25 , 0.2 ,
0.16666667, 0.14285714, 0.125 , 0.11111111, 0.1 ],
[0.5 , 0.33333333, 0.25 , 0.2 , 0.16666667,
0.14285714, 0.125 , 0.11111111, 0.1 , 0.09090909],
[0.33333333, 0.25 , 0.2 , 0.16666667, 0.14285714,
0.125 , 0.11111111, 0.1 , 0.09090909, 0.08333333],
[0.25 , 0.2 , 0.16666667, 0.14285714, 0.125 ,
0.11111111, 0.1 , 0.09090909, 0.08333333, 0.07692308],
[0.2 , 0.16666667, 0.14285714, 0.125 , 0.11111111,
0.1 , 0.09090909, 0.08333333, 0.07692308, 0.07142857],
[0.16666667, 0.14285714, 0.125 , 0.11111111, 0.1 ,
0.09090909, 0.08333333, 0.07692308, 0.07142857, 0.06666667],
[0.14285714, 0.125 , 0.11111111, 0.1 , 0.09090909,
0.08333333, 0.07692308, 0.07142857, 0.06666667, 0.0625 ],
[0.125 , 0.11111111, 0.1 , 0.09090909, 0.08333333,
0.07692308, 0.07142857, 0.06666667, 0.0625 , 0.05882353],
[0.11111111, 0.1 , 0.09090909, 0.08333333, 0.07692308,
0.07142857, 0.06666667, 0.0625 , 0.05882353, 0.05555556],
[0.1 , 0.09090909, 0.08333333, 0.07692308, 0.07142857,
0.06666667, 0.0625 , 0.05882353, 0.05555556, 0.05263158]])array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
lrg = LinearRegression(fit_intercept=False)
lrg.fit(x, y)输出
LinearRegression(copy_X=True, fit_intercept=False, n_jobs=1, normalize=False)
r = lrg.coef_
r输出
array([-9.99828937e+00, 9.89853083e+02, -2.37568861e+04, 2.40211807e+05,
-1.26112598e+06, 3.78341267e+06, -6.72611884e+06, 7.00070032e+06,
-3.93791626e+06, 9.23713318e+05])
np.dot(x, r)输出
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
岭回归
ridge = Ridge(alpha=1, fit_intercept=False)
ridge.fit(x, y)输出
Ridge(alpha=1, copy_X=True, fit_intercept=False, max_iter=None,
normalize=False, random_state=None, solver=’auto’, tol=0.001)
r_ = ridge.coef_np.dot(x ,r_)输出
array([1.30187411, 0.8693616 , 0.67735459, 0.56190875, 0.4829164 ,
0.4247503 , 0.37981691, 0.34390419, 0.31445808, 0.2898268 ])
# logspace()alphas = np.logspace(-10, -2, 10000)
ridge = Ridge(fit_intercept=False)
# 用循环来添加alpha的值
result_ = []
for alpha in alphas:
ridge.set_params(alpha=alpha)
ridge.fit(x, y)
w_ = ridge.coef_
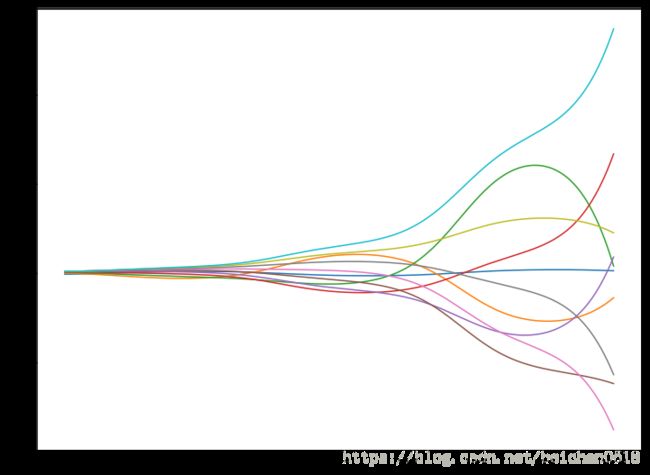
result_.append(w_)# 离散图
plt.figure(figsize=(12, 9))
plt.plot(alphas, result_)
# 将X轴的刻度,改为以log的形式呈现
plt.xscale('log')
# 获取轴面
axes = plt.axes()
# xlim
plt.xlim(axes.get_xlim()[::-1])输出
(0.025118864315095822, 3.9810717055349695e-11)
三、lasso回归
1、原理
# Lasso也在这个linear_model
from sklearn.linear_model import Lasso【拉格朗日乘数法】
对于参数w增加一个限定条件,能到达和岭回归一样的效果:
缩减系数, 缩进不重要的系数
w = [0.1, 10, 0.2, -5.5] <= 15.7(lambda)
- 最终变成[0,10, 0.2, -5.5]
- 比如说相亲,外貌,身高, 体重, 籍贯, 资产, 职业, 收入
[10, 8, 8, 1, 11, 5, 99] <= x - 数字越大,就越重要
- lasso 和 岭回归可以实现一样的效果
# Lasso alpha 取值 和 ridge 中的alpha取值是一样的
# normalize = True 可以解决数值比较大的问题
lasso = Lasso()2、实例
四、普通线性回归、岭回归与lasso回归比较
导包,导入sklearn.metrics.r2_score用于给模型打分
# 自己生成一组数据
# 现在有50行,200列,50个方程, 200个未知数,无解
sample = 50
feature = 200
x = np.random.randn(sample, feature)# 系数自己添加
w = np.random.randn(200)
# 把数据给打乱
inds = np.arange(0, 200)
np.random.shuffle(inds)
# 选取190个系数,把它变成0
w[inds[:190]] = 0
w输出
array([ 0. , 0.17755688, 0. , 0. , -1.73059122,
0. , 0. , 0.88589454, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0.19649968, 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0.66780357, 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , -0.58486057, 0. ,
0. , 0. , 0. , -1.96586347, 0. ,
0. , 0. , 0. , 0. , 0. ,
0.49664703, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0.89525249,
0.66021298, 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. ])
# y
y = np.dot(x, w)
lrg = LinearRegression()
lrg.fit(x ,y)输出
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
lrg_coef = lrg.coef_ridge = Ridge(alpha=0.1)
ridge.fit(x, y)输出
Ridge(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=None,
normalize=False, random_state=None, solver=’auto’, tol=0.001)
ridge_coef = ridge.coef_lasso = Lasso(alpha=0.1)
lasso.fit(x, y)输出
Lasso(alpha=0.1, copy_X=True, fit_intercept=True, max_iter=1000,
normalize=False, positive=False, precompute=False, random_state=None,
selection=’cyclic’, tol=0.0001, warm_start=False)
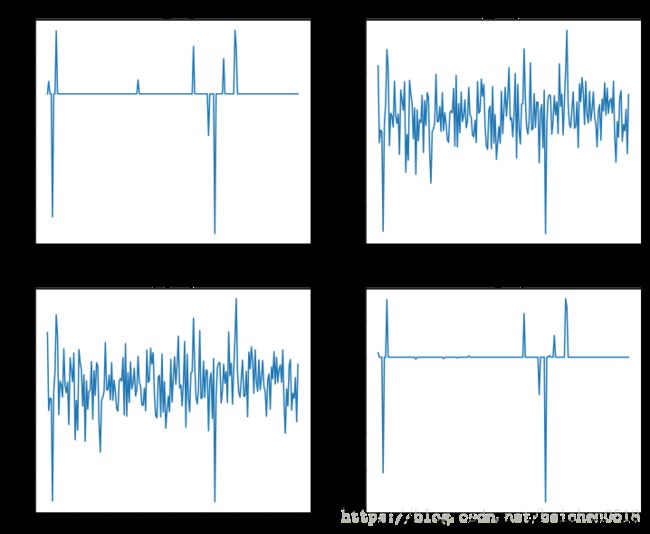
lasso_coef = lasso.coef_# 画图,原来的系数,线性回归得到的系数
# 岭回归得到的系数, 罗斯回归得到系数
plt.figure(figsize=(2 * 6, 2 * 5))
# 真实的值
axes = plt.subplot(2,2,1)
axes.plot(w)
axes.set_title('True_weight')
# 线性回归的到系数
axes1 = plt.subplot(2,2,2)
axes1.plot(lrg_coef)
axes1.set_title('lrg_weight')
# 岭回归的到系数
axes1 = plt.subplot(2,2,3)
axes1.plot(ridge_coef)
axes1.set_title('ridge_weight')
# 罗斯回归的到系数
axes1 = plt.subplot(2,2,4)
axes1.plot(lasso_coef)
axes1.set_title('lasso_weight')Text(0.5,1,'lasso_weight')