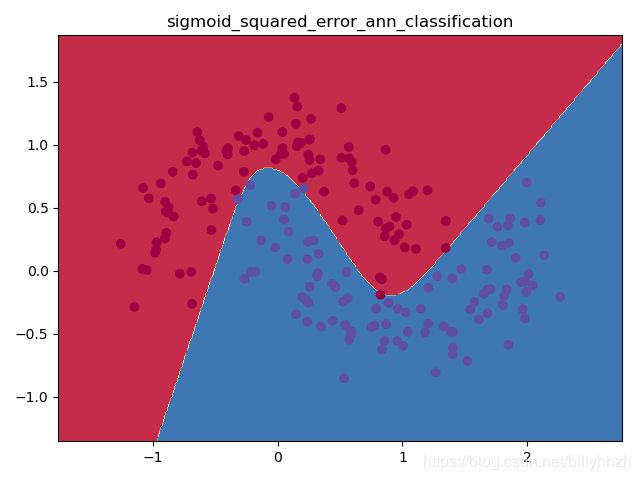
Python3神经网络,经典简单示例sigmoid激活函数

选用了sigmoid作为激活函数，作为输出层的计算(多分类版本的logistic回归)，影响输出层的delta计算；

选用了squared-error作为损失函数(注：会影响calculate_loss函数的计算以及输出层的delta计算)

 

__author__ = 'http://clayandgithub.github.io/'
import numpy as np
from sklearn import datasets, linear_model
import matplotlib.pyplot as plt

class NNModel:
    Ws = [] # params W of the whole network
    bs = [] # params b of the whole network
    layers = [] # number of nodes in each layer
    epsilon = 0.01 # default learning rate for gradient descent
    reg_lambda = 0.01 # default regularization strength

    def __init__(self, layers, epsilon = 0.01, reg_lambda = 0.01):
        self.layers = layers
        self.epsilon = epsilon
        self.reg_lambda = reg_lambda
        self.init_params()

    # Initialize the parameters (W and b) to random values. We need to learn these.
    def init_params(self):
        np.random.seed(0)
        layers = self.layers
        hidden_layer_num = len(layers) - 1
        Ws = [1] * hidden_layer_num
        bs = [1] * hidden_layer_num
        for i in range(0, hidden_layer_num):
            Ws[i] = np.random.randn(layers[i], layers[i + 1]) / np.sqrt(layers[i])
            bs[i] = np.zeros((1, layers[i + 1]))
        self.Ws = Ws
        self.bs = bs

    # This function learns parameters for the neural network from training dataset
    # - num_passes: Number of passes through the training data for gradient descent
    # - print_loss: If True, print the loss every 1000 iterations
    def train(self, X, y, num_passes=20000, print_loss=False):
        num_examples = len(X)
        expected_output = self.transform_output_dimension(y)

        # Gradient descent. For each batch...
        for i in range(0, num_passes):

            # Forward propagation
            a_output = self.forward(X)

            # Backpropagation
            dWs, dbs = self.backward(X, expected_output, a_output)

            # Update parameters of the model
            self.update_model_params(dWs, dbs, num_examples)

            # Optionally print the loss.
            # This is expensive because it uses the whole dataset, so we don't want to do it too often.
            if print_loss and i % 1000 == 0:
                print("Loss after iteration %i: %f" % (i, self.calculate_loss(X, expected_output)))

    # Helper function to evaluate the total loss on the dataset
    def calculate_loss(self, X, expected_output):
        output_shape = expected_output.shape
        num_output = output_shape[0]#training set size
        dimension_output =  output_shape[1]# output dimension

        # Forward propagation to calculate our predictions
        a_output = self.forward(X)
        current_output = a_output[-1]

        # Calculating the loss
        data_loss = np.sum(np.square(current_output - expected_output) / 2)
        # Add regulatization term to loss (optional)
        for W in self.Ws:
            data_loss += self.reg_lambda / 2 * np.sum(np.square(W))
        return 1. / num_output * data_loss

    # Forward propagation
    def forward(self, X):
        Ws = self.Ws
        bs = self.bs
        hidden_layer_num = len(Ws)
        a_output = [1] * hidden_layer_num
        current_input = X

        for i in range(0, hidden_layer_num - 1):
            w_current = Ws[i]
            b_current = bs[i]
            z_current = current_input.dot(w_current) + b_current
            a_current = sigmoid(z_current)
            a_output[i] = a_current
            current_input = a_current

        #output layer(logistic)
        z_current = current_input.dot(Ws[hidden_layer_num - 1]) + bs[hidden_layer_num - 1]
        a_current = sigmoid(z_current)
        a_output[hidden_layer_num - 1] = a_current
        return a_output

    # Predict the result of classification of input x
    def predict(self, x):
        a_output = self.forward(x)
        return np.argmax(a_output[-1], axis=1)

    # Backpropagation
    def backward(self, X, expected_output, a_output):
        Ws = self.Ws
        bs = self.bs
        hidden_layer_num = len(Ws)
        num_examples = len(X)
        ds = [1] * hidden_layer_num

        # output layer
        a_current = a_output[-1]
        d_current = -(expected_output - a_current) * a_current * (1 - a_current)
        ds[hidden_layer_num - 1] = d_current

        #other hidden layer
        for l in range(hidden_layer_num - 2, -1, -1):
            w_current = Ws[l + 1]
            a_current = a_output[l]
            d_current = np.dot(d_current, w_current.T) * a_current * (1 - a_current)
            ds[l] = d_current

        #calc dW && db
        dWs = [1] * hidden_layer_num
        dbs = [1] * hidden_layer_num
        a_last = X
        num_output = len(X)
        for l in range(0, hidden_layer_num):
            d_current = ds[l]
            dWs[l] = np.dot(a_last.T, d_current)
            dbs[l] = np.sum(d_current, axis=0, keepdims=True)
            a_last = a_output[l]
        return dWs, dbs

    # Update the params (Ws and bs) of the netword during Backpropagation
    def update_model_params(self, dWs, dbs, num_examples):
        Ws = self.Ws
        bs = self.bs
        hidden_layer_num = len(Ws)
        for l in range(0, hidden_layer_num):
            Ws[l] = Ws[l] - self.epsilon * (dWs[l] + self.reg_lambda * Ws[l])
            bs[l] = bs[l] - self.epsilon * (dbs[l])
            #Ws[l] = Ws[l] - self.epsilon * (dWs[l] / num_examples + model.reg_lambda * Ws[l])
            #bs[l] = bs[l] - self.epsilon * (dbs[l] / num_examples)
        self.Ws = Ws
        self.bs = bs

    # tranform the label matrix to output matrix (i.e. [0, 1, 1]->[[1, 0], [0, 1], [0, 1]])
    def transform_output_dimension(self, y):
        class_num = np.max(y) + 1 # start with 0
        examples_num = len(y)
        output = np.zeros((examples_num, class_num))
        output[range(examples_num), y] += 1
        return output

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def generate_data(random_seed, n_samples):
    np.random.seed(random_seed)
    X, y = datasets.make_moons(n_samples, noise=0.20)
    return X, y

def visualize(X, y, model):
    plt.title("sigmoid_squared_error_ann_classification")
    plot_decision_boundary(lambda x:model.predict(x), X, y)

def plot_decision_boundary(pred_func, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole gid
    Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)
    plt.show()

class Config:
    # Gradient descent parameters
    epsilon = 0.01  # learning rate for gradient descent
    reg_lambda = 0.01  # regularization strength
    layers = [2, 4, 2] # number of nodes in each layer

def main():
    X, y = generate_data(6, 200)
    model = NNModel(Config.layers, Config.epsilon, Config.reg_lambda)
    model.train(X, y, print_loss=True)
    visualize(X, y, model)

if __name__ == "__main__":
    main()

 

结果：

Loss after iteration 0: 0.251743
Loss after iteration 1000: 0.085999
Loss after iteration 2000: 0.043758
Loss after iteration 3000: 0.031237
Loss after iteration 4000: 0.028426
Loss after iteration 5000: 0.027443
Loss after iteration 6000: 0.027016
Loss after iteration 7000: 0.026799
Loss after iteration 8000: 0.026676
Loss after iteration 9000: 0.026602
Loss after iteration 10000: 0.026555
Loss after iteration 11000: 0.026525
Loss after iteration 12000: 0.026505
Loss after iteration 13000: 0.026491
Loss after iteration 14000: 0.026481
Loss after iteration 15000: 0.026474
Loss after iteration 16000: 0.026468
Loss after iteration 17000: 0.026464
Loss after iteration 18000: 0.026461
Loss after iteration 19000: 0.026458