二叉树的遍历方式（递归）

二叉树的遍历方式（递归）

博客摘要：

博客链接：非递归遍历二叉树

1.什么是二叉树的遍历？ 四种遍历是什么?
2.递归的实现二叉树的遍历； （下一篇博客将讲述三种遍历的非递归实现）

一. 什么是二叉树

简述：二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。

例如下图：

二.四种遍历

本篇博客讲述二叉树的四种遍历：前序遍历，中序遍历，后序遍历，层序遍历；

1.前序遍历：先访问当前结点，再访问当前结点的左子树结点，最后访问当前结点的右子树的结点；
2.中序遍历：先左再中（代表当前结点的意思）最后右结点；
3.后序遍历：先左再右最后中；
4.层序遍历：望文生义，就是一层一层的遍历，默认每层左到右遍历；

例如：

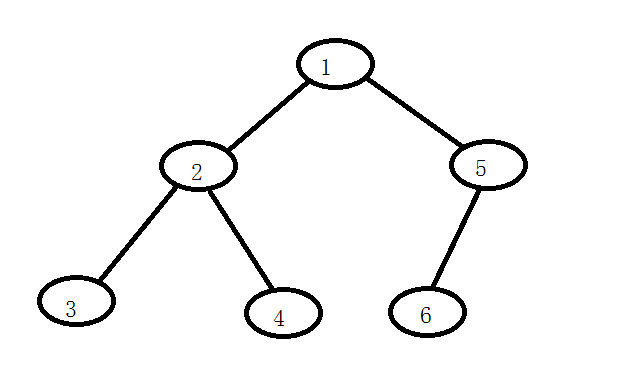
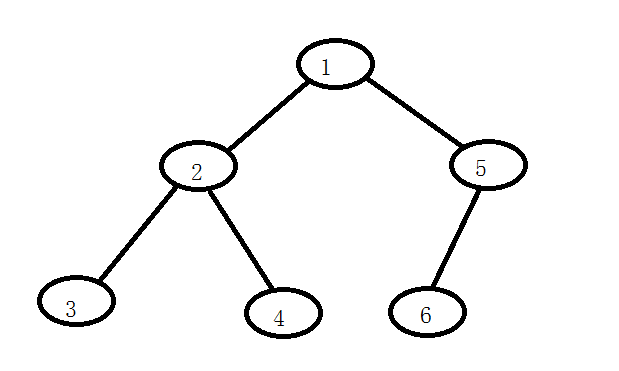
这棵二叉树的四种遍历结果：
//前序遍历：1 2 3 4 5 6
//中序遍历：3 2 4 1 6 5
//后序遍历：3 4 2 6 5 1
//层序遍历：1 2 5 3 4 6

三.递归的实现遍历

首先，我们得有一棵二叉树，我们给出一个序列，先通过这个序列构造出一颗二叉树：

int array[10] = {1,2,3,’#’,’#’,4,’#’,’#’,5, 6 };

//构造出结点
template<class T> //模板
struct BinaryNode
{
    T _data;             //数据
    BinaryNode* _left;   //左孩子
    BinaryNode* _right;  //右孩子

    BinaryNode (const T& x)
        :_data(x)
        ,_left (NULL)
        ,_right (NULL)
    {}

};

然后需要构造出二叉树，构造二叉树时我们也需要一种顺序来构造，一般默认为前序；
template
class BinaryTree
{
public:
typedef BinaryNode* Node; //重命名，为了敲代码方便

BinaryTree ()  
    :_root(NULL)
{}
//带参数的构造函数
BinaryTree (T* a, size_t size, const T& invalid)
{
    assert(a);
    size_t index = 0;
    //在这里我先不实现具体代码，GreateTree()函数代表构造好一颗二叉树；
    _root = GreateTree(a, size, invalid, index);
}

//拷贝构造；
BinaryTree (const BinaryTree & tree)
{

    _root = new BinaryNode (tree._root->_data);

    Node root = tree._root ;
    //_BinarryTree()代表拷贝构造好一颗二叉树（具体代码在最后面）；
    _BinaryTree(_root,root);
}

private:
Node _root;
}

//为什么我在这里不先实现构造的具体代码，是因为，我们要讲几种遍历，现在只需要了解大体框架就好；

看了上面的大体框架之后，我们就可以开始递归遍历的具体算法实现了；

//下面的这些函数都是实现在protected修饰的下面的，都需要用公有的方法去调用，为了安全；
比如：

public:

void PosOrder()
{
     _PosOrder(_root);//调用
     cout<

//前三种遍历的递归实现很简单，我就直接写下来了，可以根据遍历的概念理解；

//后序遍历
    void _PosOrder(Node root)
    {
        if(root == NULL)
            return;
        _PosOrder (root->_left );//先左孩子
        _PosOrder (root->_right );//再右孩子
        cout<<root->_data <<" ";//最后中；
    }

//中序遍历
    void _InOrder(Node root)
    {
        if(root ==  NULL)
            return;

        _InOrder(root->_left);
        cout<<root->_data <<" ";
        _InOrder(root->_right);
    }

//前序遍历
    void _PrevOrder(Node root)
    {
        if(root == NULL)
            return;

        cout<<root->_data <<" ";

        _PrevOrder(root->_left);
        _PrevOrder (root->_right );
    }

//层序遍历的话就需要具体的说一下了，层序遍历需要用队列来辅助实现；

//首先，层序遍历：一层一层的遍历，就例如上面给出的那个例子，层序遍历的结果是：1，2，5，3，4，6；
可以看出来是先把1访问了，再访问它的左右孩子，然后再以2为父节点访问它的左右孩子，然后是5的组有孩子；

依据这个规律我们可以借助队列来实现，队列是先进先出的，那么，我们先让1进入队列，然后将1的左右孩子依次放进队列，访问队头结点，以此类推；

过程如下：

先把根结点（最顶层的那个结点）放入队列；

如果队列不为空；
queue(队列)：1；
访问队头元素；
1 的左右孩子（如果不为NULL）依次放入队列：
queue:1 2 5;
删除队头；

如果队列不为空；
queue：2 5；
访问队头元素2；
2的左右孩子（如果不为NULL）依次放入队列：
queue: 5 3 4;
删除队头；

如果队列不为空；
queue：5 3 4；
访问队头元素5；
5的左右孩子（如果不为NULL）依次放入队列：
queue: 5 3 4 6;
删除队头；

如果队列不为空；
queue：3 4 6；
访问队头元素3；
3的左右孩子（如果不为NULL）依次放入队列：
queue: 3 4 6;
删除队头；

如果队列不为空；
queue：4 6；
访问队头元素4；
4的左右孩子（如果不为NULL）依次放入队列：
queue: 4 6;
删除队头；

如果队列不为空；
queue：6；
访问队头元素6；
6的左右孩子（如果不为NULL）依次放入队列：
queue: ;
删除队头；

如果队列不为空；
此时队列为空，结束！

层序遍历
    void LevelOrder1()
    {
        queue q;
        q.push (_root);

        while(!q.empty ())
        {
            Node top = q.front ();
            cout<_data <<" ";
            q.pop ();
            if(top->_left )
                q.push (top->_left );
            if(top->_right )
                q.push (top->_right );


        }
    }