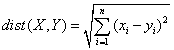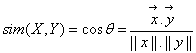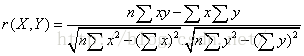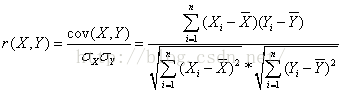浅谈聚类&层次聚类

浅谈聚类

引言

         聚类分析的目标就是在相似的基础上收集数据来分类。即聚类是我们在面对于大量数据时，所常采用的一种数据处理方式。通过，使用聚类方法有助于将原有数据进行划分，初步将其分为不同部分，提升对于数据的宏观认识，为深入理解数据打下基础。

         聚类算法在工业界有着巨大的应用，如在<数学之美>一书中，即举Google将其应用于新闻分类的例子。近年，尤其随着机器学习的火热，聚类算法在学术界与工业界均得到了极大的重视。如2015年初，Science即发表一kmeans聚类改进算法。

         从统计学的观点看，聚类分析是通过数据建模简化数据的一种方法。

         从机器学习的角度讲，簇相当于隐藏模式。聚类是搜索簇的无监督学习过程。

 

 

 

聚类与分类(判别)

         单从名字中来看，聚类与分类差别不大。但不论放之于统计或机器学习中其差别巨大。用一句常语"物以类聚，人以群分"，则是对于聚类分析与分类的最直观简明的诠释。

         从理论上而言，在机器学习中，聚类与分类最大的区别在于是否有监督的学习，即是否存在训练集，即分类(判别)方法具有训练集，通过训练集训练模型进而得到分类模型，再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现分类的目的，也就具有了对未知数据进行分类的能力。而聚类则常不具有训练集，也即是说事先没有任何训练样本，而需要直接对数据进行建模。

         在统计学中，聚类分析。根据研究对象特征对研究对象进行分类的一种多元分析技术, 把性质相近的个体归为一类, 使得同一类中的个体都具有高度的同质性, 不同类之间的个体具有高度的异质性。而分类(判别) 是一种进行统计判别和分组的技术手段。根据一定量案例的一个分组变量和相应的其他多元变量的已知信息, 确定分组与其他多元变量之间的数量关系, 建立判别函数, 然后便可以利用这一数量关系对其他未知分组类型所属的案例进行判别分组。

         也即是随聚类与分类名称类似，但实际其为完全不同的两个概念，所处理的数据也是截然不同的。

主要聚类思想与方法

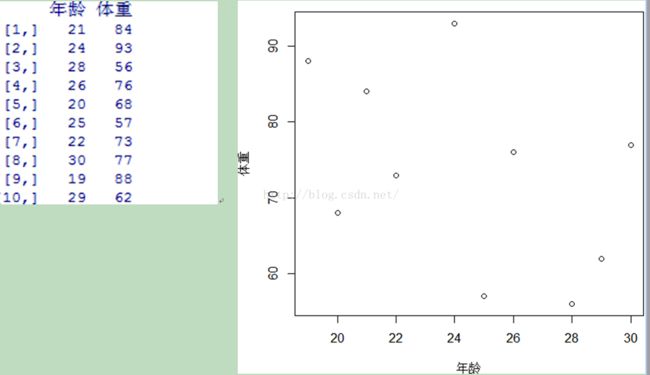
         谈起聚类，首先，在此我们假设一个简单的情景即假设我们需要将某一体育课程学生进行聚类，那么我们将如何完成对于所选学生的划分呢？在此，为简单过程，我们在此假设学生仅具有两种属性即年龄与体重。下面本文将结合各主要聚类思想与算法基于R语言给大家详细介绍：

1 层次聚类

        

         层次聚类是我们在聚类过程中常用的一种方法，其主要思想是：

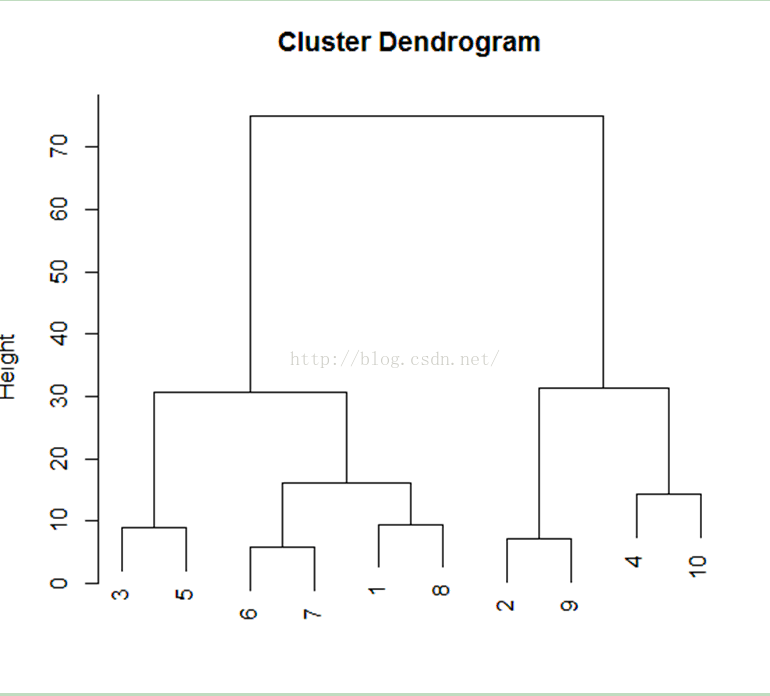
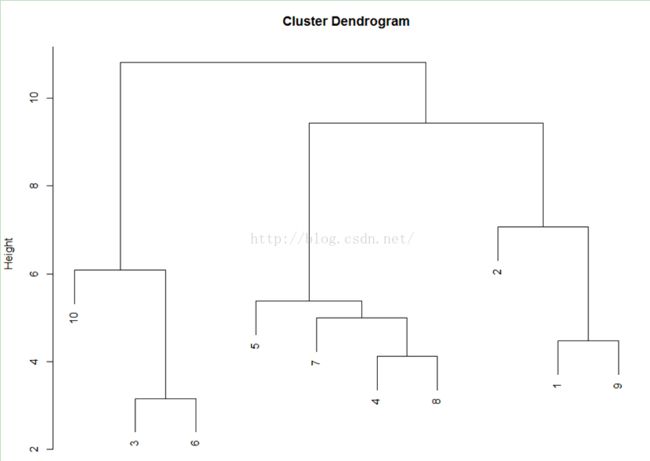
         即将聚类样本中的个体间关系远近使用距离来进行代替,将距离相近的样本放之于一类，重复此过程即可完成聚类。一般采取的聚类过程为自下而上，上图即为一层次聚类过程图，所谓自下而上，也即是一开始样本比如在y轴0层时，都是各自的个体，随着聚类的进行，样本逐渐聚合知道最后形成一类。（另一种为自顶而下，大家可以百度一下）。

         在具体计算中为了寻找距离最近/远和均值，都需要对所有的距离计算个遍，需要用到双重循环，且每次迭代都只能合并两个子类，这是非常慢的，但此方法一般满足日常使用，R中自带的层次聚类函数hclust即此种方法。

         在此，我们提到了距离，那么这里的距离指的是什么呢？在此我们引入统计学中计算样本相似性的各种距离:

1.1相似度计算

1.11距离概念

         欧几里得距离(EuclideanDistance)

　　欧氏距离是最常见的距离度量，衡量的是多维空间中各个点之间的绝对距离。公式如下：

　　因为计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标使用欧式距离可能使结果失效。

 

明可夫斯基距离(Minkowski Distance)

　　明氏距离是欧氏距离的推广，是对多个距离度量公式的概括性的表述。公式如下：

　　这里的p值是一个变量，当p=2的时候就得到了上面的欧氏距离。

 

曼哈顿距离(Manhattan Distance)

　　曼哈顿距离来源于城市区块距离，是将多个维度上的距离进行求和后的结果，即当上面的明氏距离中p=1时得到的距离度量公式，如下：

 

切比雪夫距离(Chebyshev Distance)

　　切比雪夫距离起源于国际象棋中国王的走法，我们知道国际象棋国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格(x1, y1)走到B格(x2, y2)最少需要走几步？扩展到多维空间，其实切比雪夫距离就是当p趋向于无穷大时的明氏距离：

　　其实上面的曼哈顿距离、欧氏距离和切比雪夫距离都是明可夫斯基距离在特殊条件下的应用。

 

1.12相似度度量

　　相似度度量（Similarity），即计算个体间的相似程度，与距离度量相反，相似度度量的值越小，说明个体间相似度越小，差异越大。

 

向量空间余弦相似度(Cosine Similarity)

　　余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量，余弦相似度更加注重两个向量在方向上的差异，而非距离或长度上。公式如下：

 

皮尔森相关系数(Pearson Correlation Coefficient)

　　即相关分析中的相关系数r，分别对X和Y基于自身总体标准化后计算空间向量的余弦夹角。公式如下：

也即为

        

 

1.2聚类过程

         假设有N个待聚类的样本，对于层次聚类来说，基本步骤就是：

       1、（初始化）把每个样本归为一类，计算每两个类之间的距离，也就是样本与样本之间的相似度；

       2、按一定规则选取符合距离要求的类别，完成类间合并；

       3、重新计算新生成的这个类与各个旧类之间的相似度；

       4、重复2和3直到所有样本点都归为一类，结束。

 

         在这里如果细心会发现在步骤二过程中出现了按一定规则选取这一细节，在此我们简单介绍一下聚类过程中常用的选取规则。

 

Single 方法：

         选取两类与中，距离最短的节点x与y，然后以此距离作为此两类的距离。然后将具有最短距离的类别相合并。

Complete方法：

         选取两类与中，距离最长的节点x与y，然后以此距离作为此两类的距离。然后将具有最短距离的类别相合并。

Average 方法：

         选取两类与中，所有节点的平均距离，然后以此距离作为此两类的距离。然后将具有最短距离的类别相合并。

Centorid方法：

         选取两类与的类中中心点(即重心)，计算两类中心的差的平方，以此作为距离。

Ward最小方差法：

         此方法并类时总是使得并类导致的类内离差平方和增量最小。即首先,n个样本各程一类，每次类合并则总离差平方和就要增加，选择使离差平方和增加最小的两类进行合并。

         在R中，此方法被分为两种分别为Ward与Ward.D2两种方法，此两种的差别在于Ward.D2方法在类更新前将离差进行了平方。

 

一般我们在应用中，选择的主要方式为ward与Average方法

 

 

选择好，适合的方法后，那么我们接下来就可以开始完成聚类了。

 

以本文前面的例子为基础，在此我们进行聚类

首先，我们求取数据的距离矩阵

 

我们在R中使用的函数为dist(),其默认采用的距离为欧氏距离

dist(x,method = "euclidean", diag = FALSE, upper = FALSE, p = 2)

在此x代表所要计算距离的数据，method代表计算距离所要使用的方法，diag代表是否为包含对角线元素,upper代表是否为上三角矩阵，p则代表Minkowski距离中的p取值大小。

 

得到了距离矩阵后，为了便于理解我们使用最简单的single方法完成聚类过程，即按类间最小距离完成聚类。

在此我们使用的函数为hclust()

其默认参数为：

hclust(d, method = "complete", members = NULL)

其中d代表所要提供的距离矩阵，method代表所要使用的聚类手段，更详细的介绍可在R中?hclust查看帮助。

rect.hclust(plot,k=3)同时，可使用此函数在图中获取所需要类。其中plot代表聚类结果，k=n代表需要的类别。

通过距离矩阵，我们知道最小的距离首先为3到6的3.162287，也即是我们在上图中HEIGHT所对应2得到的第一类。然后仅次于其距离最小的为4到8的4.123106。依照此原理，逐步合并点，直至将其合并为一类则完成聚类过程。

分析。

参考文献：
邓海燕. 聚类分析与判别分析的区别[J]. 武汉学刊, 2006, (1).

Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191):1492-1496.

数学之美  吴军

数据挖掘：概念与技术（英文版·第3版） (英语) 韩家炜 (作者), 坎伯(Kamber.M.) (作者), 裴健 (作者)

图灵程序设计丛书:R语言实战  卡巴科弗 (RobertI.Kabacoff) (作者),  高涛 (译者) 

博客：http://blog.csdn.net/jwh_bupt/article/details/7685809

博客：http://www.cnblogs.com/emanlee/archive/2012/02/28/2371273.html

博客：http://blog.csdn.net/yillc/article/details/6746509