机器学习算法之Boosting算法原理和GBDT原理推导

针对Boosting的基本介绍在我的这篇文章中详细介绍了https://blog.csdn.net/blank_tj/article/details/82229322

简单总结Boosting：初始对每个样本分配相同的权重，每次经过分类，把对的结果的权重降低，错的结果权重增高，如此往复，直到阈值或者循环次数。

梯度提升算法首先给定一个目标损失函数，它的定义域是所有可行的弱函数集合(基函数)；提升算法通过迭代的选择一个负梯度方向上的基函数来逐渐逼近局部极小值。这种在函数域的梯度提升观点对机器学习的很多领域有深刻影响。

提升的理论意义：如果一个问题存在弱分类器,则可以通过提升的办法得到强分类器。

简单理解GBDT：假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

---

Boosting算法推导：

给定输入向量X和输出变量Y组成的若干训练样本， (x1,y1),(x2,y2),...,(xn,yn) ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) ，目标是找到近似函数 F^(x⃗ ) F ^ ( x → ) ，使得损失函数 L(y,F(x⃗ )) L ( y , F ( x → ) ) 的损失值最小。

L(y,F(x⃗ )) L ( y , F ( x → ) ) 的典型定义为：

L(y,F(x⃗ ))=12(y−F(x⃗ ))2 L ( y , F ( x → ) ) = 1 2 ( y − F ( x → ) ) 2

L(y,F(x⃗ ))=|y−F(x⃗ )| L ( y , F ( x → ) ) = | y − F ( x → ) |

假定最优函数为 F∗(x⃗ ) F ∗ ( x → ) ，即：

F∗(x⃗ )=argminE(x,y)[L(y,F(x⃗ ))] F ∗ ( x → ) = a r g m i n E ( x , y ) [ L ( y , F ( x → ) ) ]

假定 F(x⃗ ) F ( x → ) 是一组基函数 fi(x⃗ ) f i ( x → ) 的加权和：

F(x⃗ )=∑Mi=1γifi(x⃗ )+C F ( x → ) = ∑ i = 1 M γ i f i ( x → ) + C

梯度提升方法寻找最优解 F(x⃗ ) F ( x → ) ，使得损失函数在训练集上的期望最小。
首先，给定常函数 F0(x⃗ ) F 0 ( x → ) ：

F0(x⃗ )=argmin∑ni=1L(yi,c) F 0 ( x → ) = a r g m i n ∑ i = 1 n L ( y i , c )

以贪心思路扩展到 Fm(x⃗ ) F m ( x → )

Fm(x⃗ )=Fm−1(x⃗ )+argmin∑ni=1L(yi,Fm−1(x⃗ i)+f(x⃗ i) F m ( x → ) = F m − 1 ( x → ) + a r g m i n ∑ i = 1 n L ( y i , F m − 1 ( x → i ) + f ( x → i )

贪心法每次选择最优基函数 f f 时仍然困难，使用梯度下降的方法近似计算。将样本带入基函数 f f 得到 f(x⃗ 1),f(x⃗ 2),...,f(x⃗ n) f ( x → 1 ) , f ( x → 2 ) , . . . , f ( x → n ) ，从而 L L 退化为向量 L(y1,f(x⃗ 1)),L(y2,f(x⃗ 2)),...,L(yn,f(x⃗ n)) L ( y 1 , f ( x → 1 ) ) , L ( y 2 , f ( x → 2 ) ) , . . . , L ( y n , f ( x → n ) )

Fm(x⃗ )=Fm−1(x⃗ )+γm∑ni=1ΔfL(yi,Fm−1(x⃗ i)) F m ( x → ) = F m − 1 ( x → ) + γ m ∑ i = 1 n Δ f L ( y i , F m − 1 ( x → i ) )

上式中的权值 γ γ 为梯度下降的步长，使用线性搜索求最优步长：

γm=argmin∑ni=1L(yi,Fm−1(x⃗ i)−γ∗ΔfL(yi,Fm−1(x⃗ i))) γ m = a r g m i n ∑ i = 1 n L ( y i , F m − 1 ( x → i ) − γ ∗ Δ f L ( y i , F m − 1 ( x → i ) ) )

步骤如下：
（1）初始给定模型为常数 F0(x⃗ ) F 0 ( x → ) ，对于 m=1 m = 1 到 M M ：
（2）计算伪残差：

γim=[∂L(yi,F(x⃗ i))∂F(x⃗ i)]F(x⃗ )=Fm−1 (x⃗ ) γ i m = [ ∂ L ( y i , F ( x → i ) ) ∂ F ( x → i ) ] F ( x → ) = F m − 1   ( x → ) ， i=1,2,...,n i = 1 , 2 , . . . , n

（3）使用数据 (x⃗ i,γim)ni=1 ( x → i , γ i m ) i = 1 n 计算拟合残差的基函数 fm(x) f m ( x )
（4）计算步长

γm=argmin∑ni=1L(yi,Fm−1(x⃗ i)−γ∗fm(x⃗ i)) γ m = a r g m i n ∑ i = 1 n L ( y i , F m − 1 ( x → i ) − γ ∗ f m ( x → i ) )

（5）更新模型

Fm(x⃗ )=Fm−1(x⃗ )−γmfm(x⃗ i) F m ( x → ) = F m − 1 ( x → ) − γ m f m ( x → i )

GBDT算法推导

用公式来表达：在 GBDT G B D T 的迭代中，假设我们前一轮迭代得到的强学习器是 ft−1(x) f t − 1 ( x ) , 损失函数是 L(y,ft−1(x)) L ( y , f t − 1 ( x ) ) , 我们本轮迭代的目标是找到一个 CART C A R T 回归树模型的弱学习器 ht(x) h t ( x ) ，让本轮的损失 L(y,ft(x)=L(y,ft−1(x)+ht(x)) L ( y , f t ( x ) = L ( y , f t − 1 ( x ) + h t ( x ) ) 最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。

GBDT选取了平方损失，并用损失函数的负梯度来拟合本轮损失的近似值。第t轮的第i个样本的损失函数的负梯度为：

rti=−[∂L(yi,f(xi))∂f(xi)]f(x)=ft−1(x) r t i = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f t − 1 ( x )

经过负梯度拟合得到了 y−fxi y − f x i ，这就是我们最终要去拟合的，也叫作残差。

算法图：

GBDT算法流程：

1）初始化弱学习器：

f0(x)=argminγ∑Ni=1L(yi,γ) f 0 ( x ) = a r g m i n γ ∑ i = 1 N L ( y i , γ )

2）对迭代轮数m=1,2,…M有：
对每个样本 i=1,2,...,N i = 1 , 2 , . . . , N ，计算负梯度，即残差：

rim=−[∂L(yi,f(xi))∂f(xi)]f(x)=fm−1 (x) r i m = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f m − 1   ( x )

将上步得到的残差作为样本新的真实值，并将数据 (xi,rim)(i=1,2,...,N) ( x i , r i m ) ( i = 1 , 2 , . . . , N ) 作为下棵树的训练数据，得到一颗新的回归树 fm(x) f m ( x ) 其对应的叶子结点区域为 Rjm,j=1,2,...,J R j m , j = 1 , 2 , . . . , J 。其中 J J 为回归树t的叶子节点的个数。

对叶子区域 j=1,2,..,J j = 1 , 2 , . . , J 计算最佳拟合值：

γjm=argmin∑xi∈RjmL(yi,fm−1(xi)+γ) γ j m = a r g m i n ∑ x i ∈ R j m L ( y i , f m − 1 ( x i ) + γ )

更新强学习器：

fm(x)=fm−1(x)+∑Jj=1γjmI(x∈Rjm) f m ( x ) = f m − 1 ( x ) + ∑ j = 1 J γ j m I ( x ∈ R j m )

3）得到强学习器

f(x)=fM(x)=f0(x)+∑Mm=1∑Jj=1γjmI(x∈Rjm) f ( x ) = f M ( x ) = f 0 ( x ) + ∑ m = 1 M ∑ j = 1 J γ j m I ( x ∈ R j m )

---

GBDT 算法的实例讲解

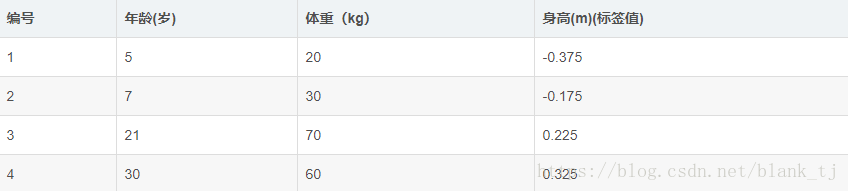
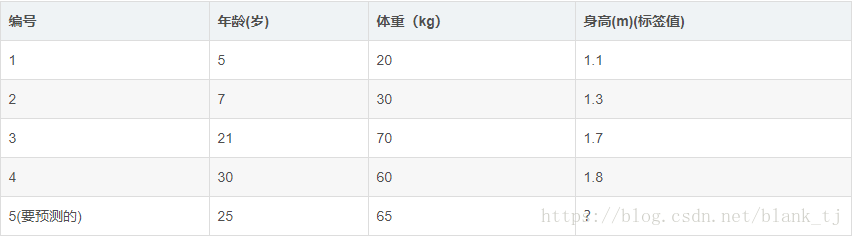
如下表所示：一组数据，特征为年龄、体重，身高为标签值。共有5条数据，前四条为训练样本，最后一条为要预测的样本。

1：初始化弱学习器：

f0(x)=argminγ∑Ni=1L(yi,γ) f 0 ( x ) = a r g m i n γ ∑ i = 1 N L ( y i , γ )

由于此时只有根节点，样本1,2,3,4都在根节点，此时要找到使得平方损失函数最小的参数Υ，怎么求呢？平方损失显然是一个凸函数，直接求导，倒数等于零，得到Υ。

∂L(yi,γ)∂γ=∂(12|y−γ|2)∂γ=γ−y ∂ L ( y i , γ ) ∂ γ = ∂ ( 1 2 | y − γ | 2 ) ∂ γ = γ − y
令 γ−y=0 γ − y = 0 ，得 γ=y γ = y 。

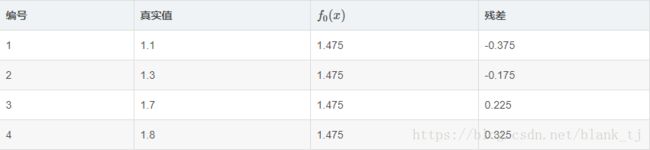
所以初始化时， γ γ 为所有训练样本标签值的均值。 γ=(1.1+1.3+1.7+1.8)/4=1.475 γ = ( 1.1 + 1.3 + 1.7 + 1.8 ) / 4 = 1.475 ，此时得到的初始学习器 f0(x) f 0 ( x )
f0(x)=γ=1.475 f 0 ( x ) = γ = 1.475

---

2:对迭代轮数m=1：
计算负梯度——残差

ri1=−[∂L(yi,f(xi))∂f(xi)]f(x)=f0 (x) r i 1 = − [ ∂ L ( y i , f ( x i ) ) ∂ f ( x i ) ] f ( x ) = f 0   ( x )

说白了，就是残差，在此例中，残差在下表列出：

此时将残差作为样本的真实值训练 f1(x) f 1 ( x ) ，即下表数据

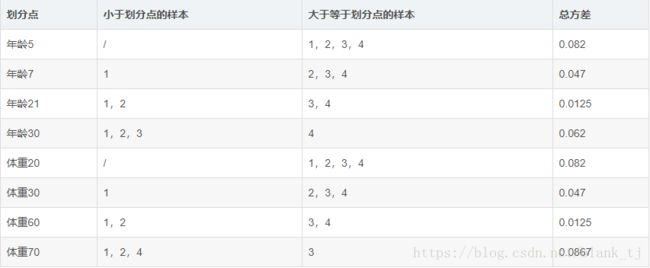
接着，寻找回归树的最佳划分节点，遍历每个特征的每个可能取值。从年龄特征的5开始，到体重特征的70结束，分别计算方差，找到使方差最小的那个划分节点即为最佳划分节点。
例如：以年龄7为划分节点，将小于7的样本划分为一类，大于等于7的样本划分为另一类。样本1为一组，样本2，3，4为一组，两组的方差分别为0，0.047，两组方差之和为0.047。所有可能划分情况如下表所示：

以上划分点是的总方差最小为0.0125有两个划分点：年龄21和体重60，所以随机选一个作为划分点，这里我们选年龄21。
此时还需要做一件事情，给这两个叶子节点分别赋一个参数，来拟合残差。

γj1=argmin∑xi∈Rj1L(yi,f0(xi)+γ) γ j 1 = a r g m i n ∑ x i ∈ R j 1 L ( y i , f 0 ( x i ) + γ )

这里其实和上面初始化学习器是一个道理，平方损失，求导，令导数等于零，化简之后得到每个叶子节点的参数Υ，其实就是标签值的均值。
根据上述划分节点：
样本1，2为左叶子节点， (x1,x2∈R11) ( x 1 , x 2 ∈ R 11 ) ，所以 γ11=(−0.375−0.175)/2=−0.275。 γ 11 = ( − 0.375 − 0.175 ) / 2 = − 0.275 。
样本3，4为左叶子节点， (x3,x4∈R11) ( x 3 , x 4 ∈ R 11 ) ，所以 γ21=(0.225+0.325)/2=0.275。 γ 21 = ( 0.225 + 0.325 ) / 2 = 0.275 。
此时可更新强学习器

f1(x)=f0(x)+∑2j=1γj1I(x∈Rj1) f 1 ( x ) = f 0 ( x ) + ∑ j = 1 2 γ j 1 I ( x ∈ R j 1 )

---

3：对迭代轮数m=2,3,4,5,…,M：
循环迭代M次，M是人为控制的参数，迭代结束生成M棵树

---

4：得到最后的强学习器：
为了方别展示和理解，我们假设Ｍ＝１，根据上述结果得到强学习器：

f(x)=fM(x)=f0(x)+∑Mm=1∑Jj=1γjmI(x∈Rjm)=f0(x)+∑2j=1γj1I(x∈Rj1) f ( x ) = f M ( x ) = f 0 ( x ) + ∑ m = 1 M ∑ j = 1 J γ j m I ( x ∈ R j m ) = f 0 ( x ) + ∑ j = 1 2 γ j 1 I ( x ∈ R j 1 )

如图所示得到只迭代一次，只有一颗树的GBDT：

---

5：预测样本5：

样本5在根节点中（即初始学习器）被预测为1.475，样本5的年龄为25，大于划分节点21岁，所以被分到了右边的叶子节点，同时被预测为0.275。此时便得到样本5的最总预测值为1.75。

---

参考了一篇非常不错的博客：https://blog.csdn.net/zpalyq110/article/details/79527653