Deep Learning（深度学习）之（六）【深度神经网络压缩】Deep Compression （ICLR2016 Best Paper）

      Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman coding

这篇论文是Stanford的Song Han的 ICLR2016 的 best paper，Song Han写了一系列网络压缩的论文，这是其中一篇，更多论文笔记也会在后续博客给出。

首先，给这篇论文的清晰结构点赞，论文题目就已经概括了文章的三个重点，而且每个部分图文并茂，文章看起来一点都不费力，不愧是 ICLR 2016 best paper !

摘要

为什么要压缩网络？

做过深度学习的应该都知道，NN大法确实效果很赞，在各个领域轻松碾压传统算法，不过真正用到实际项目中却会有很大的问题：

1. 计算量非常巨大；
2. 模型特别吃内存；

这两个原因，使得很难把NN大法应用到嵌入式系统中去，因为嵌入式系统资源有限，而NN模型动不动就好几百兆。所以，计算量和内存的问题是作者的motivation；

如何压缩？

论文题目已经一句话概括了：

1. Prunes the network：只保留一些重要的连接；
2. Quantize the weights：通过权值量化来共享一些weights；
3. Huffman coding：通过霍夫曼编码进一步压缩；

效果如何？

Pruning：把连接数减少到原来的 1/13~1/9； 
Quantization：每一个连接从原来的 32bits 减少到 5bits；

最终效果： 
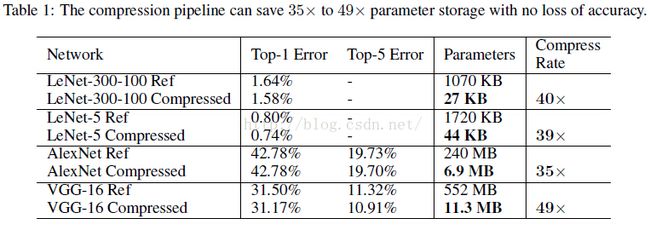
- 把AlextNet压缩了35倍，从 240MB，减小到 6.9MB； 
- 把VGG-16压缩了49北，从 552MB 减小到 11.3MB； 
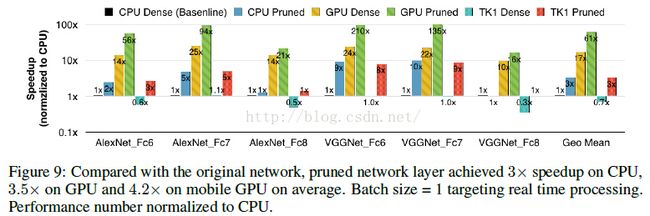
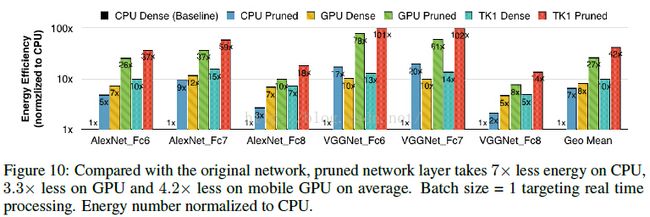
- 计算速度是原来的3~4倍，能源消耗是原来的3~7倍；

Network Pruning

       其实 network pruning 技术已经被广泛应用到CNN模型的压缩中了。 早期的一些工作中，LeCun 用它来减少网络复杂度，从而达到避免 over-fitting 的效果； 近期，其实也就是作者的第一篇网络压缩论文中，通过剪枝达到了 state-of-the-art 的结果，而且没有减少模型的准确率；

从上图的左边的pruning阶段可以看出，其过程是：

1. 正常的训练一个网络；
2. 把一些权值很小的连接进行剪枝：通过一个阈值来剪枝；
3. retrain 这个剪完枝的稀疏连接的网络；

     为了进一步压缩，对于weight的index，不再存储绝对位置的index，而是存储跟上一个有效weight的相对位置，这样index的字节数就可以被压缩了。 
     论文中，对于卷积层用 8bits 来保存这个相对位置的index，在全连接层中用 5bits 来保存；

    上图是以用3bits保存相对位置为例子，当相对位置超过8（3bits）的时候，需要在相对位置为8的地方填充一个0，防止溢出；

Trained Quantization and Weight Sharing

     前面已经通过权值剪枝，去掉了一些不太重要的权值，大大压缩了网络； 为了更进一步压缩，作者又想到一个方法：权值本身的大小能不能压缩？

答案当然是可以的，具体怎么做请看下图：

       假设有一个层，它有4个输入神经元，4个输出神经元，那么它的权值就是4*4的矩阵； 图中左上是weight矩阵，左下是gradient矩阵。可以看到，图中作者把 weight矩阵 聚类成了4个cluster（由4种颜色表示）。属于同一类的weight共享同一个权值大小（看中间的白色矩形部分，每种颜色权值对应一个cluster index）；由于同一cluster的weight共享一个权值大小，所以我们只需要存储权值的index 例子中是4个cluster，所以原来每个weight需要32bits，现在只需要2bits，非常简单的压缩了16倍。而在 权值更新 的时候，所有的gradients按照weight矩阵的颜色来分组，同一组的gradient做一个相加的操作，得到是sum乘上learning rate再减去共享的centroids，得到一个fine-tuned centroids，这个过程看上图，画的非常清晰了。

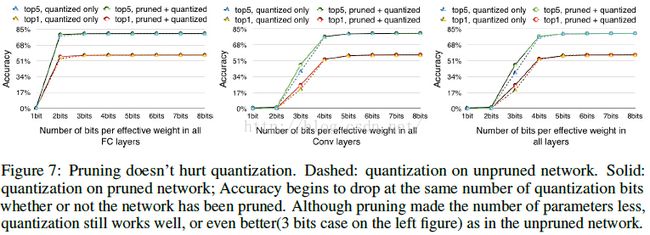
       实际中，对于AlexNet，卷积层quantization到8bits（256个共享权值），而全连接层quantization到5bits（32个共享权值），并且这样压缩之后的网络没有降低准确率

Weight Sharing

       具体是怎么做的权值共享，或者说是用什么方法对权值聚类的呢？

其实就用了非常简单的 K-means，对每一层都做一个weight的聚类，属于同一个 cluster 的就共享同一个权值大小。 注意的一点：跨层的weight不进行共享权值；

Initialization of Shared Weights

       做过 K-means 聚类的都知道，初始点的选择对于结果有着非常大的影响，在这里，初始点的选择同样会影响到网络的性能。作者尝试了很多生产初始点的方法：Forgy(random), density-based, and linear initialization。

       画出了AlexNet中conv3层的权重分布，横坐标是权值大小，纵坐标表示分布，其中红色曲线表示PDF（概率密度分布），蓝色曲线表示CDF（概率密度函数），圆圈表示的是centroids：黄色（Forgy）、蓝色（density-based）、红色（linear）。

      作者提到：大的权值往往比小的权值起到更重要的作用，不过，大的权值往往数量比较少；可以从图中看到，Forgy 和 density-based 方法产生的centroids很少落入到大权值的范围中，造成的结果就是忽略了大权值的作用；而Linear initialization产生的centroids非常平均，没有这个问题存在；

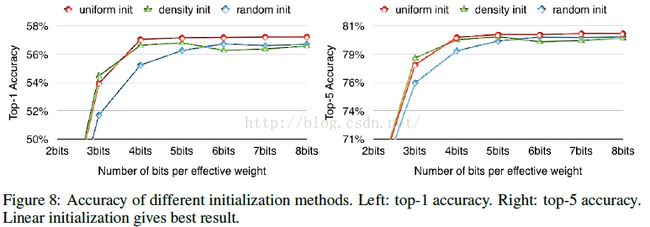
后续的实验结果也表明，Linear initialization 的效果最佳。

Huffman Coding

      Huffman Coding 是一种非常常用的无损编码技术。它按照符号出现的概率来进行变长编码。

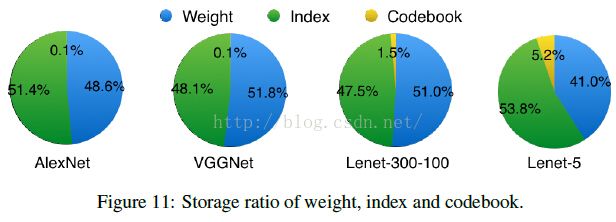
      上图的权重以及权值索引分布来自于AlexNet的最后一个全连接层。由图可以看出，其分布是非均匀的、双峰形状，因此我们可以利用Huffman编码来对其进行处理，最终可以进一步使的网络的存储减少20%~30%。

Experiment Results

   

        简单贴一个最终得到的模型跟BVLC baseline 和其他基于alexnet的压缩网络的性能对比：

更详细内容，请参考原文。