【TensorFlow】优化方法optimizer总结（SGD，Adagrad，Adadelta，Adam，Adamax，Nadam）解析（十三）

本文仅对一些常见的优化方法进行直观介绍和简单的比较，主要是一阶的梯度法，包括SGD, Momentum, Nesterov Momentum, AdaGrad, RMSProp, Adam。 其中SGD,Momentum,Nesterov Momentum是手动指定学习速率的,而后面的AdaGrad, RMSProp, Adam,就能够自动调节学习速率。

1、SGD

SGD全名 stochastic gradient descent， 即随机梯度下降。不过这里的SGD其实跟MBGD(minibatch gradient descent)是一个意思，现在的SGD一般都指mini-batch gradient descent，即随机抽取一批样本,以此为根据来更新参数。

具体实践：

需要:学习速率 ϵ, 初始参数 θ
每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差并更新参数:

优点:

1. 训练速度快,对于很大的数据集,也能够以较快的速度收敛.SGD应用于凸问题时，k次迭代后泛化误差的数量级是O(1/sqrt(k))，强凸下是O(1/k)。
2. 可能由于SGD在学习中增加了噪声，有正则化的效果

缺点: 由于是抽取,因此不可避免的,得到的梯度肯定有误差.因此学习速率需要逐渐减小.否则模型无法收敛 ，因为误差,所以每一次迭代的梯度受抽样的影响比较大,也就是说梯度含有比较大的噪声,不能很好的反映真实梯度.

ϵ学习率如何衰减以保证SGD收敛，在实践中，一般是进行线性衰减: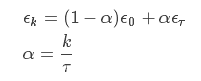

其中ϵ0是初始学习率, ϵτ是最后一次迭代的学习率. τ自然代表迭代次数.一般来说,ϵτ 设为ϵ0的1%比较合适.而τ一般设为让训练集中的每个数据都输入模型上百次比较合适.那么初始学习率ϵ0怎么设置呢?书上说,你先用固定的学习速率迭代100次,找出效果最好的学习速率,然后ϵ0设为比它大一点就可以了.

2、Momentum

SGD方法的一个缺点是，其更新方向完全依赖于当前的batch，因而其更新十分不稳定，每次迭代计算的梯度含有比较大的噪音。解决这一问题的一个简单的做法便是引入momentum。

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力。

具体实现:

需要:学习速率 ϵ, 初始参数 θ, 初始速率v, 动量衰减参数α

每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差,并更新速度v和参数θ:

其中参数α表示每回合速率v的衰减程度.如果每次迭代得到的梯度都是g,那么最后得到的v的稳定值为：

也就是说,Momentum最好情况下能够将学习速率加速1/(1−α)倍.一般α的取值有0.5,0.9,0.99这几种，分别表示最大速度2倍，10倍，100倍于SGD的算法。.当然,也可以让α的值随着时间而变化,一开始小点,后来再加大.不过这样一来,又会引进新的参数.

特点:
- 前后梯度方向一致时,能够加速学习
- 前后梯度方向不一致时,能够抑制震荡

3、Nesterov Momentum

这是对传统momentum方法的一项改进，由Ilya Sutskever(2012 unpublished)在Nesterov工作的启发下提出的。

具体实现:

需要:学习速率 ϵ, 初始参数 θ, 初始速率v, 动量衰减参数α
每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差,并更新速度v和参数θ:
   注意在估算梯度g的时候,参数变成了θ+αv而不是之前的θ，与Momentum唯一区别就是，计算梯度的不同，Nesterov先用当前的速度v更新一遍参数，在用更新的临时参数计算梯度。

其基本思路如下图（转自Hinton的coursera公开课lecture 6a）：

4、AdaGrad

AdaGrad可以自动变更学习速率,只是需要设定一个全局的学习速率ϵ,但是这并非是实际学习速率,实际的速率是与以往参数的模之和的开方成反比的.也许说起来有点绕口,不过用公式来表示就直白的多:

其中δ是一个很小的常亮,大概在10^−7,防止出现除以0的情况.

具体实现:
需要:全局学习速率 ϵ, 初始参数 θ, 数值稳定量δ
中间变量: 梯度累计量r(初始化为0)

每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差,更新r,再根据r和梯度计算参数更新量:
   

优点: 能够实现学习率的自动更改。如果这次梯度大,那么学习速率衰减的就快一些;如果这次梯度小,那么学习速率衰减的慢一些。对于每个参数，随着其更新的总距离增多，其学习速率也随之变慢。

缺点: 任然要设置一个变量ϵ ,经验表明，在普通算法中也许效果不错，但在深度学习中，深度过深时会造成训练提前结束。

5、RMSProp

RMSProp通过引入一个衰减系数，让r每回合都衰减一定比例，类似于Momentum中的做法，是对AdaGrad算法的改进。

具体实现:
需要:全局学习速率 ϵ, 初始参数 θ, 数值稳定量δ，衰减速率ρ
中间变量: 梯度累计量r(初始化为0)

每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差,更新r,再根据r和梯度计算参数更新量：
   

优点：
- 相比于AdaGrad,这种方法很好的解决了深度学习中过早结束的问题
- 适合处理非平稳目标，对于RNN效果很好

缺点：
- 又引入了新的超参，衰减系数ρ
- 依然依赖于全局学习速率

6、RMSProp with Nesterov Momentum

此方法是将RMSProp和Nesterov Momentum结合起来

具体实现:
需要:全局学习速率 ϵ, 初始参数 θ, 初始速率v，动量衰减系数α, 梯度累计量衰减速率ρ
中间变量: 梯度累计量r(初始化为0)

每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差,更新r,再根据r和梯度计算参数更新量 ：
   

7、Adam

Adam(Adaptive Moment Estimation)本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。

具体实现:
需要:步进值 ϵ, 初始参数 θ, 数值稳定量δ，一阶动量衰减系数ρ1, 二阶动量衰减系数ρ2
其中几个取值一般为：δ=10^−8,ρ1=0.9,ρ2=0.999
中间变量：一阶动量s，二阶动量r,都初始化为0

每步迭代过程:

1. 从训练集中的随机抽取一批容量为m的样本{x1,…,xm},以及相关的输出yi
2. 计算梯度和误差,更新r和s,再根据r和s以及梯度计算参数更新量 ：
   

8、各个方法的比较

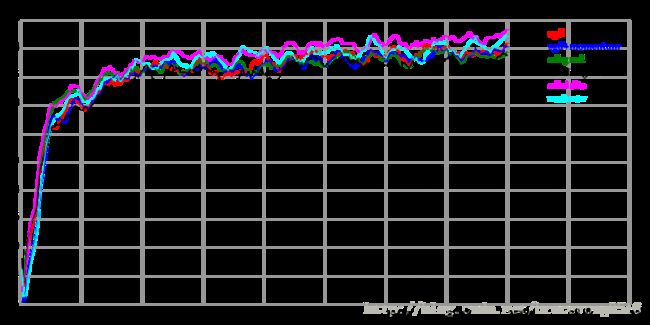
Karpathy做了一个这几个方法在MNIST上性能的比较，其结论是：

adagrad相比于sgd和momentum更加稳定，即不需要怎么调参。而精调的sgd和momentum系列方法无论是收敛速度还是precision都比adagrad要好一些。在精调参数下，一般Nesterov优于momentum优于sgd。而adagrad一方面不用怎么调参，另一方面其性能稳定优于其他方法。

Loss vs. Number of examples seen

Testing Accuracy vs. Number of examples seen

Training Accuracy vs. Number of examples seen