DRL之DQN Deep Q Network 学习总结
本次总结从最底下的Ref Links的material中得来,如果对于某些细节不清楚可以看看链接中的内容。我在看10-703的视频的时候,我觉得Russ讲课还是很不错的,很多东西讲得言简意赅,短短几句就把DQN的核心讲得清楚。
RL中核心的三个东西:policy,model和value function。policy就是根据当前的state进行对应的action,当然可以是deterministic(确定的,一对一)或者是stochastic的(概率的)表示。一般来说,当state表示为离散的,action space比较小的时候使用确定的比较合适,效果比较好。value function是描述一个state和action的好坏,通过value function我们可以推出policy,因为我们的目标是最大化reward,reward的expectation越大,那么value就越大。model就是对environment的建模,有了model,就可以simulate experience,就可以增加experience的数目,可以用MC和TD得到value function和policy。在这个基础上,如果把real experience和simulated experience一起计算value function和policy,就叫做dyna。
对于value function在进一步,因为这是DQN的重点。value function就是对未来的总的reward的一个expectation。value function分为state-value function和action-value function,state-value function就是对在policy π 下,处于state St 的expectation total reward。action-value function就是在某个policy下,执行action的一个total reward expectation。此处对于这两个function的具体计算可以看David的Lecture 2(多看几遍就清楚了)。
对于action-value function也叫Q-value function,因为它用字母Q表示了action-value function。具体可以表示为如下式子:
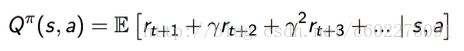
上诉式子可以写成Bellman equation来表示:s’ 就是在s进行action之后的状态。

如果我们可以找到optimal的Q-value function,那么就可以得到policy,就是在state s的执行怎么样的action才适合,才能最大化value。
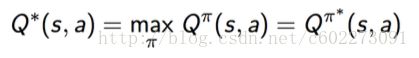
当然,根据Bellman Equation可以得到,因为reward是固定的,所以应该maximize是下一个state的Q value。
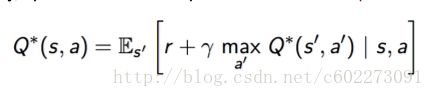
我们可以发现在这样的情况下,求得optimal value maximize就是求解每一步都要maximize reward(下面的公式这里说的是使用greedy的策略,为的是表示这种想法,要最大化的reward的意思)

到目前为止了,我就把三个要点policy,model,value function介绍了一下。在RL领域,有value-based RL(在任何的policy下进行最大化maximum value function,对应policy evaluation),policy-based RL(直接进行policy优化,其实就是policy improvement,进行greedy的policy改进,看David的Lecture 3),model-based RL(对environment进行建模,那么就可以进行planning,就是知道在state s进行action之后的reward和state,也就是MDP的state transition和reward,那么问题就变成了已知MDP,如何最大化reward,使用随机策略的policy evaluation就可以)。同时,如果得到了model,就可以得到simulation experience。
今天要讲的呢是对Q-value function进行estimation,如何进行approximation呢?那么就要找到一个近似函数,使得:
![]()
这种approximation可以有以下形式,输入s,a,然后estimate Q。或者输入state,estimate Q。当然,有了Q-value,那么可以选取Q-value最大的action作为接下来的action,那么policy也就出来了。
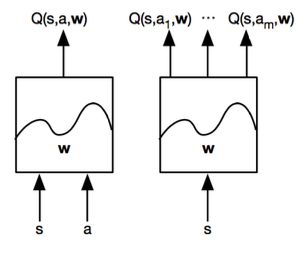
既然是这种approximation,那么我们的目标函数是是神马呢?根据刚才说的Bellman equation可以使用以下作为target value,你会发现这个就是TD Q-value。你说用MC可以不可以,当然是更好了,但是总的来说,使用TD的话,可以得到大量的experience,方便训练,使用MC的话,时间会比较长,需要整个episode。

到这里,DQN的大致的loss function已经呼之欲出,就是用某个函数approximation Q-value function,但是在目前的训练中,上面的loss function是有问题的,就是它的target居然会随着w变化,那么就会导致很难对target进行拟合,这种unstable的loss是不适合训练的。所以这里就需要对target进行保留一段时间来让approximation function进行拟合。所以在loss里面保留了两套的w,一个是旧的w,一个新的w。如果进行了固定次的新的w的更新以后,就把新的w付给旧的。这就是所谓的不同步的w,通过这样的方法来解决non-stationarity的问题。保留transition( st,at,rt+1,st+1 ,然后使用旧的weight的计算的target作为target,用新的w进行拟合,用stochastic gradient descent进行计算)

现在有了loss function,接下来就是选定approximation model,那么可以选择现在用烂了的CNN。比如下图中就是输入四帧,然后输出18个action的value,也就是Q(s,a)。

reward就是该时刻的输出和上一个的差值就可以计算出reward。这里有一个DQN代码的例子:【6】。
DQN中有人提出了Double Q-Learning,这个东西就是使用有两个action-value,Q1和Q2。使用Q1的value来更新Q2,使用Q2的value来更新Q1。然后action的选择使用 ?-greedy。

那么这种Double DQN用什么用呢,可以使用这种方法来表示刚才说的DQN中的新旧的w,这种对偶训练有很好的效果,在Atari中使用Double的DQN比DQN好很多,效果好很多。
在训练的过程中,有人觉得针对不同的experience应该有不同的权重,对于error小的experience应该更不需要改进,对于error大的权重更需要改变。所以权重的改进可以采用下面的公式:

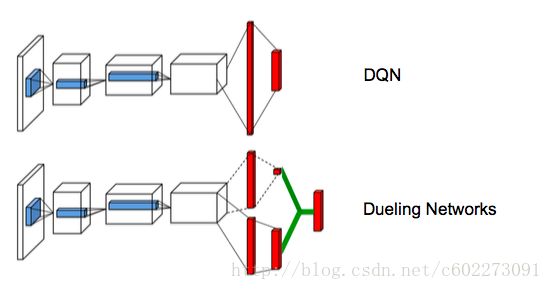
另外,有人对网络结构进行改变,叫做Dueling Networks,我觉得这个灵感很可能来自于R-CNN。网络分为action-independent value function V(s,v)和action-dependent advantage function A(s,a,w)。

advantage function是衡量了某个action的好坏,会对状态的改变有attention。value stream是对状态敏感。
另外,目前还有可以进行多任务的DQN,就是训练一个DQN可以同时打多个游戏(multitask DQN)还有一个叫做transfer learning,就是把已经训练好的参数迁移到新的task上面,在进行fine-tune。
转载请注明出处: http://blog.csdn.net/c602273091/article/details/79029848
Ref Links:
[1] DQN Part1: https://www.youtube.com/watch?v=iKq2P5Cbohw
[2] DQN Part2: https://www.youtube.com/watch?v=ZlVxuoCMV4I
[3] CMU 10-703 DQN: http://www.cs.cmu.edu/~rsalakhu/10703/Lecture_DQL.pdf
[4] David Silver DRL: http://videolectures.net/rldm2015_silver_reinforcement_learning/
[5] David Silver DRL Tutorial: https://icml.cc/2016/tutorials/deep_rl_tutorial.pdf
[6] Code example: https://sites.google.com/a/deepmind.com/dqn/