算法设计与分析：Minimum Number of Refueling Stops（Week 11）

学号：16340008

题目：871. Minimum Number of Refueling Stops

---

Question:

A car travels from a starting position to a destination which is target miles east of the starting position.

Along the way, there are gas stations.  Each station[i] represents a gas station that is station[i][0] miles east of the starting position, and has station[i][1] liters of gas.

The car starts with an infinite tank of gas, which initially has startFuel liters of fuel in it.  It uses 1 liter of gas per 1 mile that it drives.

When the car reaches a gas station, it may stop and refuel, transferring all the gas from the station into the car.

What is the least number of refueling stops the car must make in order to reach its destination?  If it cannot reach the destination, return -1.

Note that if the car reaches a gas station with 0 fuel left, the car can still refuel there.  If the car reaches the destination with 0 fuel left, it is still considered to have arrived.

 

Example 1:

Input: target = 1, startFuel = 1, stations = []
Output: 0
Explanation: We can reach the target without refueling.

Example 2:

Input: target = 100, startFuel = 1, stations = [[10,100]]
Output: -1
Explanation: We can't reach the target (or even the first gas station).

Example 3:

Input: target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
Output: 2
Explanation: 
We start with 10 liters of fuel.
We drive to position 10, expending 10 liters of fuel.  We refuel from 0 liters to 60 liters of gas.
Then, we drive from position 10 to position 60 (expending 50 liters of fuel),
and refuel from 10 liters to 50 liters of gas.  We then drive to and reach the target.
We made 2 refueling stops along the way, so we return 2.

 

Note:

1. 1 <= target, startFuel, stations[i][1] <= 10^9
2. 0 <= stations.length <= 500
3. 0 < stations[0][0] < stations[1][0] < ... < stations[stations.length-1][0] < target

---

Answer:

题意大致如下：在起点给定油量startFuel，stations中每个元素[a,b]表示距离起点a处可补充油量b，油量与里程1：1，问最少能加油多少次到距离target的终点（不能则返回-1）。我们可以假定起点为[0,startFuel]，于是问题可以化成多个子问题再对比。对于每个油站，我们都当成子问题的起点，例如第一个油站stations[0]——[a,b]，我们可以当成是起点油量为startFuel1 = startFuel0 - a + b，距离终点target1 = target0 - a的子问题。前提是可以从起点到达第一个油站（即startFuel0 >= a）。

于是对于一个问题，我们作如下操作：

1. 检查能否直接到达终点，可以则直接返回0
2. 检查从起点有没有可以到达的油站，如果没有则返回油站数+1（方便直接比较加油次数），有则记录每个可达油站
3. 对每个可达油站，建立子问题，其startFuel = startFuel - a + b，target = target - a，对每个子问题执行步骤1、2、3，对它们的返回数取最小值+1并返回。

然而在写代码的过程中，发现这样需要对每次求解子问题创造一个数组更新起点与加油站的距离，或者记录该起点与原始起点的距离，这需要修改原递归函数的参数。而且这种方法将会呈树状分散，而且树的节点难以重用，因为前面加油方式的改变将改变该次加油的状态（剩余油量），显然没有发挥动态规划的优点和特性。

再次观察题目可以发现，实际上题目与背包问题十分类似。0/1背包问题为给定权重不同的物品，容量定的背包，求能获得的最大价值。其将问题分为子问题：拿了物品后的剩余物品与容量，不拿物品的剩余物品与容量，取大值（假设能拿）。此处可以效仿。0/1背包问题用一个二维数组dp[i][j]存储在容量为j，面对是否拿第i件物品时能获得的最大值。此题同样一个二维数组，存储在第i个油站时加j次油能走的最远距离，那么在最后一个油站时加最少次油能到target的j值就是所求值。

对于数组中一个值dp[i][j]，我们有：

得到最初代码（python3）：

class Solution:
    def minRefuelStops(self, target, startFuel, stations):
        """
        :type target: int
        :type startFuel: int
        :type stations: List[List[int]]
        :rtype: int
        """
        n = len(stations)
        if n == 0:
            if target <= startFuel:
                return 0
            else:
                return -1
        dp = [[0 for i in range(n + 1)] for i in range(n + 1)]

        dp[0][0] = startFuel

        for i in range(1, n + 1):
            if startFuel >= stations[i-1][0]:
                dp[i][0] = startFuel
        
        for i in range(1, n + 1):
            for j in range(1, i + 1):
                dp[i][j] = max(dp[i-1][j] if dp[i-1][j] >= stations[i-1][0] else 0, dp[i-1][j-1] + stations[i-1][1] if dp[i-1][j-1] >= stations[i-1][0] else 0)
        for i in range(n + 1):
            if dp[n][i] >= target:
                return i
        
        return -1

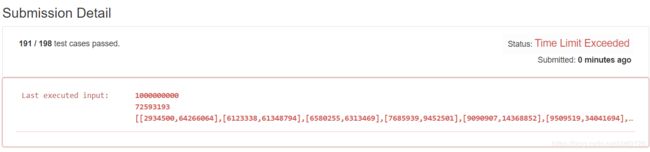
然而代码遇到了TLE：

因为二维数组其实不必填满。在上面的代码中二维数组是横向填充，一行一行从左往右从上往下填，时间复杂度为O(n)，然而如果竖向填充，则可能可以在填满前即可到达target的情况。

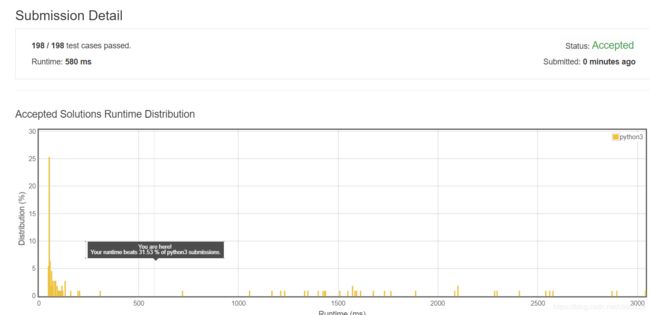
因此把代码改为竖向填充（实际则交换二层嵌套循环的i与j），并在每列填充结束时检验能否到达target ，即可应付station很多的情况（需要测例不极端，极端则优化前后没有区别）。

改进代码如下（python3）：

class Solution:
    def minRefuelStops(self, target, startFuel, stations):
        """
        :type target: int
        :type startFuel: int
        :type stations: List[List[int]]
        :rtype: int
        """
        n = len(stations)
        if startFuel >= target:
            return 0
        dp = [[0 for i in range(n + 1)] for i in range(n + 1)]

        dp[0][0] = startFuel


        for i in range(1, n + 1):
            if startFuel >= stations[i-1][0]:
                dp[i][0] = startFuel
        
        for j in range(1, n + 1):
            for i in range(j, n + 1):
                dp[i][j] = max(dp[i-1][j] if dp[i-1][j] >= stations[i-1][0] else 0, dp[i-1][j-1] + stations[i-1][1] if dp[i-1][j-1] >= stations[i-1][0] else 0)
            if dp[n][j] >= target:
                return j
        
        return -1

提交结果如下：