Fast R-CNN论文学习

Abstract

这篇论文提出了针对目标识别的Fast Region-based Convolution Network(Fast R-CNN)方法。Fast R-CNN训练速度要比R-CNN快9倍，测试速度要快213倍，而且在PASCAL VOC2012数据集上的mAP要更高。与SPPnet相比，Fast R-CNN训练速度快3倍，测试速度快10倍，而且更准确。

1. Introduction

目标检测要比图像分类麻烦很多，当前的方法一般都是通过多阶段流程来训练，不仅慢还不优雅。

识别物体需要精确的定位，这就有两个麻烦之处。首先要得到粗糙的候选目标位置（叫proposals）；其次，这些候选位置仅是提供了大概的位置，需要精确定位它们。这篇论文提出了一个单阶段训练算法，结合地学习目标候选位置，并优化其空间位置。

1.1 R-CNN 和 SPPnet

R-CNN的问题

• 训练需要多阶段流程：先在目标proposals上微调一个CNN，然后用SVM来做目标检测器。在第三阶段，还要学习bounding-box regressors。
• 训练空间成本和时间成本高：特征需要从每张图像上的目标proposals提取出，然后写到磁盘。
• 目标检测速度慢：用VGG16在GPU上检测，每张图像要47秒。

SPPnet的改进和问题

R-CNN慢因为它需要在每个proposal上都跑一遍CNN，没有共享计算。SPPnet（空间金字塔池化网络）则共享了计算，测试速度快了10到100倍，训练速度也快了3倍。SPPnet先对每张图像计算一个卷积特征图，然后再用特征图里提取的特征向量来对每个proposal做分类。在特征图上max-pooling每个proposal对应的部分，提取特征作为一个固定长度的输出。多个不同大小的输出然后在空间金字塔池化中拼接起来。

SPPnet的问题：它也是多阶段流程训练，需要提取特征，微调网络，训练SVM，最后还要bounding-box regressors. 而且何凯明论文中的SPPnet无法更新空间金字塔池化层之前的卷积层，这也影响了深度网络的准确度。

1.2 本论文的贡献

提出新的训练算法，解决R-CNN和SPPnet的问题，Fast R-CNN有以下几个优势：

• 检测准确度高；
• 单一阶段训练，使用多任务loss；
• 训练可以更新所有的网络层；
• 不需要占用磁盘空间来cache特征；

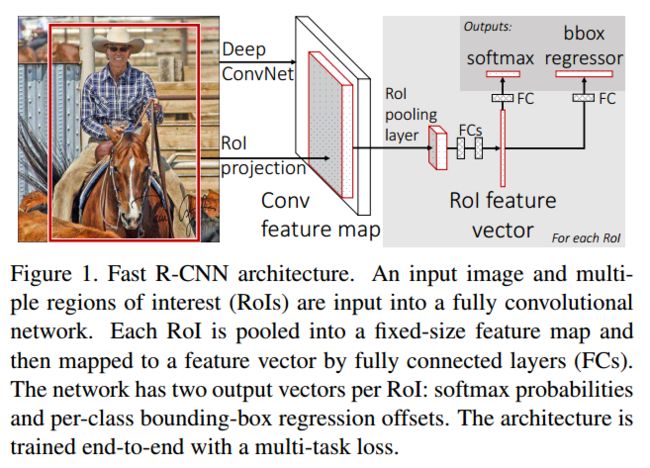
2. Fast R-CNN结构和训练

上图就是Fast R-CNN的结构。网络的输入是一整张图像和目标proposals的集合。网络首先通过几个卷积层和max pooling层处理图像，产生一张卷积特征图。然后对于每一个目标proposal，region of interest（RoI）池化层从特征图里提取一个固定长度的特征向量。每个特征向量都被输入进2个sibling全连接层：一个输出（K个类别+1个背景类别的）softmax概率，另一个输出四个实数值，代表bounding-box位置。

2.1 RoI池化层

RoI池化层使用max pooling把RoI内的特征转为固定范围（$H\times W$）的小特征图。RoI是卷积特征图上的一个矩形窗口，由4值的元组（r, c, h, w）决定位置，(r, c)决定左上角位置，(h, w)决定高和宽。RoI max pooling 把 $h\times w$的窗口分割为$H\times W$个子窗口，每个子窗口大小为$h/H\times w/W$，然后max-pool每个子窗口，把得到的值放进对应的输出网格中。RoI层其实就是空间金字塔池化层的特例，RoI只有一个金字塔level。

2.2 初始化 Pre-trained 网络

作者通过3个pre-trained ImageNet网络做实验，每个网络有5个max pooling层和5-13个卷积层，还要改动3个地方才能做Fast R-CNN：

• 最后的max pooling层要被RoI池化层替换，而且H和W的值要与第一个全连接层兼容。
• ImangeNet 网络最后的全连接层和softmax层要被替换为2个sibling的全连接层，一个是$K+1$个类别，一个是bounding-box regressor.
• 网络要改为接受两个数据输入，一个是图像，一个是图像的RoI。

2.3 Fine-tune

不同于SPPnet，Fast R-CNN整个网络可以被使用反向传播训练是一个极大的优点，而SPPnet无法更新SPP（空间金字塔池化）层以下的层。论文中作者提到SPP层中的感受野非常大，使用BP算法训练时效率低。也就是说，在一个batch训练中，你一开始RoI源于这张图片，而下一个RoI源于另一张图片。如此往复，如果ROI很大的话，这就导致在BP效率会很低。

为了解决这个问题，作者利用特征分享的优势，提出一个更加有效的训练方法：SGD mini-batches分层采样方法。在同一个batch中，为了减少图像使用量，首先选择N张图像，然后从每张图像中选择$R/N$个RoI。同一个图像里的RoI，在前向和反向传播过程中共享计算和内存。这样就很好地解决了上述问题。

前面提到了，Fast R-CNN训练是在single-stage中完成，但实际中它包含了：multi-task loss, mini-batch sampling, RoI pooling, BP throungh RoI pooling layers, SGD hyper-parameters.

Multi-task loss

Fast R-CNN网络有两个sibling输出层，第一个输出层针对每个RoI输出离散的概率分布, 在$K+1$个类上有$p=(p_0,\cdots ,p_K)$。$p$是通过softmax计算出来的。第二个sibling层输出bounding-box回归位移，$t^k=(t_x^k,t_y^k,t_w^k,t_h^k),k\in K$。

每个训练RoI都被标上其真值类别$u$和真值bounding-box回归目标$v$。作者用一个多任务损失函数$L$，在每一个标注好的RoI上共同训练分类和bounding-box回归：

$$L(p,u,t^u,v)=L_{cls}(p,u)+\lambda [u\ge 1]L_{loc}(t^u,v).$$

$[u\ge 1]$是Iverson bracket指标函数，当$u\ge 1$，它等于1，否则为0。对于背景proposal来说，$u=0$。

$$L_{cls}(p,u)=-log{p}_u.$$是类$u$的log loss。

第二个损失任务，对于类$u$，$L_{loc}$定义于bounding-box回归目标的元组（真值）上，$v=(v_x,v_y,v_w,v_h)$，和一个对于类$u$的预测元组（预测值），$t^u=(t_x^u,t_y^u,t_w^u,t_h^u)$。

对于bounding-box回归，使用：
$$L_{loc}(t^u,v)=\sum _{i\in \{x,y,w,h\}}smoot{h}_{L_1}（t_i^u-v_i).$$
$$smoot{h}_{L_1}(x)=\{\begin{array}{ll}0.5x^2& \text{if |x|<1}\\ |x|-0.5& \text{otherwise}\end{array}$$

$L(p,u,t^u,v)$中的$\lambda$是个超参数，控制两个loss tasks的平衡。所有的实验中，$\lambda =1$。

Mini-batch sampling

在微调时，每个SGD mini-batch都通过随机选择$N=2$张图像构建，然后从每张图片中选择64个RoIs。选取25%的RoIs，这些RoIs与真值bounding-box的IoU（Intersection over union）不少于0.5。这些RoIs构成了前景目标类, $u=1$。剩下的RoIs与真值bounding-box的IoU最大也就0.5，它们也就构成了背景目标类，$u=0$。

通过RoI池化层反向传播

从这篇借鉴理解RoI池化层：Fast R-CNN论文详解
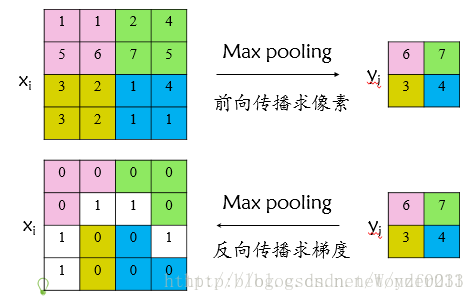
首先看普通max pooling层如何求导，设$x_i$为输入层节点，$y_i$为输出层节点，那么损失函数$L$对输入层节点$x_i$的梯度为：
$$\frac{\delta L}{\delta x_i}=\{\begin{array}{rlr}0,& & \delta (i,j)=false\\ \frac{\delta L}{\delta y_j},& & \delta (i,j)=true\end{array}$$
$\delta (i,j)$表示输入$i$节点是否被输出$j$节点选为最大值输出。

不被选中$\delta (i,j)=false$有两种可能：xi不在yi范围内，或者xi不是最大值。
若选中$\delta (i,j)=true$则由链式规则可知损失函数$L$相对$x_i$的梯度等于损失函数$L$相对$y_i$的梯度$\times$ $y_i$对$x_i$的梯度（恒等于1），故可得上述所示公式；
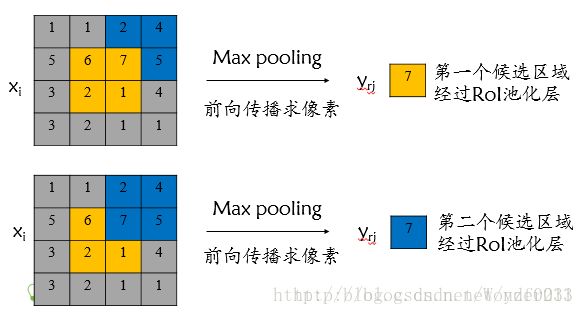
对于RoI max pooling层，设$x_i$为输入层的节点，$y_{rj}$ 为第$r$个候选区域的第$j$个输出节点，一个输入节点可能和多个输出节点相关连，如下图所示，输入节点7和两个候选区域输出节点相关连：

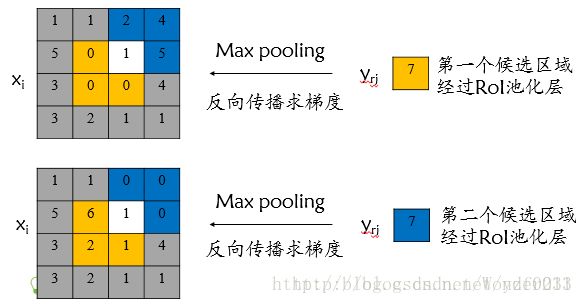
该输入节点7的反向传播如下图所示：

对于不同候选区域，节点7都存在梯度，所以反向传播中损失函数 $L$ 对输入层节点 $x_i$的梯度为损失函数 $L$ 对各个有可能的候选区域 $r$ 【 $x_i$ 被候选区域$r$的第$j$个输出节点选为最大值 】输出 $y_{rj}$ 梯度的累加，具体如下公式所示：
$$\frac{\delta L}{\delta x_i}=\sum _r\sum _j[i=i^{\ast }(r,j)]\frac{\delta L}{\delta y_{rj}}$$

$$[i=i^{\ast }(r,j)]=\{\begin{array}{rlr}1,& & i=i^{\ast }(r,j)\ge 1\\ 0,& & otherwise\end{array}$$
判决函数 $[i=i^{\ast }(r,j)]$表示第$i$个节点是否被候选区域$r$ 的第$j$ 个输出节点选为最大值输出，若是，则由链式规则可知损失函数$L$相对 $x_i$ 的梯度等于损失函数 $L$ 相对$y_{rj}$的梯度 $\times$ $y_{rj}$ 对$x_i$的梯度（恒等于1)，上图已然解释该输入节点可能会和不同的$y_{rj}$ 有关系，故损失函数$L$相对$x_i$ 的梯度为求和形式。

SGD 超参数

除了修改增加的层，原有的层参数已经通过预训练方式初始化：
用于分类的全连接层以均值为0、标准差为0.01的高斯分布初始化；
用于回归的全连接层以均值为0、标准差为0.001的高斯分布初始化。
偏置都初始化为0；

针对PASCAL VOC 2007和2012训练集，前30k次迭代全局学习率为0.001，每层权重学习率为1倍，偏置学习率为2倍，后10k次迭代全局学习率更新为0.0001。动量设置为0.9，权重衰减设置为0.0005。

2.4 Scale Invariance

实现尺度不变有两种方式：

1. “brute force”(单一尺度，原图)
2. “image pyramids”(多尺度方法)

3. Fast R-CNN 检测

3.1 SVD快速检测

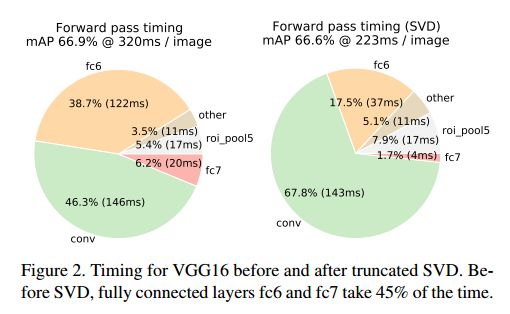
在检测的时候，RoI的数量很大，接近一半的前向时间都花在了全连接层上。全连接层可以通过SVD压缩来加速。

假设有一个层，它的权值矩阵是$u\times v$形状的$W$，它可以用SVD分解为
$$W\approx U{\Sigma }_t{V}^T$$.
$U$是形状为$u\times t$的矩阵，包含着$W$的前$t$个左奇异向量， ${\Sigma }_t$是形状为$t\times t$的对角线矩阵，由$W$的前$t$个奇异值组成，$V$是形状为$v\times t$的矩阵，对应着$W$的前$t$个右奇异向量。SVD方法把参数个数由$uv$减少到$t(u+v)$个。为了压缩一个网络，用两个全连接层来代替对应着$W$的单个全连接层。第一个层使用权值矩阵${\Sigma }_t{V}^T$，第二个使用$U$。

4. 实验结果

训练和测试时间

奇异值分解SVD