Focal Loss 论文学习

论文地址：https://arxiv.org/abs/1708.02002

Abstract

目前精度高的目标检测器都是基于一个双阶段的方案（如R-CNN），在一个候选对象位置组成的稀疏集合上应用一个分类器。相反，单阶段检测器应用于一个由候选对象位置组成的稠密集合上，速度比较快而且更简单，但是一般来说，精度不如双阶段检测器。我们发现，在训练稠密检测器时，前景-背景类别的不均衡是导致此问题的核心因素。作者提出了一种方法来解决这种类别的不平衡，通过重构传统的交叉熵损失（cross entropy loss）来降低良好分类的样本的损失值。Focal loss 在一个由困难样本（hard examples）组成的稀疏集合上训练，防止在训练时绝大多数的容易负样本（easy negative）占据主导位置。为了评价此损失函数的有效性，作者设计和训练了一个简单的稠密检测器（dense detector），叫做 RetinaNet。结果显示，用Focal loss来训练，RetinaNet 在速度上能够匹敌其他的单阶段检测器，而在精度上超过所有的主流检测器。代码放在：https://github.com/facebookresearch/Detectron

1. Introduction

目前主流的目标检测器都基于双阶段，包含候选框的机制。在R-CNN中，第一阶段产生一个候选框位置的稀疏集合，第二阶段通过一个卷积网络将每个候选位置分类为前景或背景类。这种方法在COCO基准上达到了很高的准确率。

尽管双阶段检测器精度高，但问题是单阶段检测器也能获得同样的准确率吗？单阶段检测器应用在不同物体位置，比例，和宽高比的稠密抽样上。最近的单阶段检测器，如SSD和YOLO展现了不错的成绩，速度更快，但精度仍低于双阶段检测器。

在这篇论文中，作者提出了一个单阶段检测器，它第一次地能在COCO AP上和流行的双阶段检测器在准确率上匹敌，例如特征金字塔网络（Feature Pyramid Network）或者 Mask R-CNN（Faster R-CNN变体）。作者认识到训练中的类别不平衡是阻碍单阶段检测器获取高准确率的主要障碍，因而提出了新的损失函数。

由R-CNN变形出来的检测器通过一个双阶段级联和采样启发式学习过程解决了类别不均衡问题。候选框建议阶段（如Selective search, EdgeBoxes, DeepMask, RPN等）很快地就可以把候选目标位置数量缩小到一千至两千，过滤出占大多数的背景样本。在第二个分类阶段，使用采样启发学习来保持前景和背景之间的平衡，例如固定大小的前景-背景比例（1：3），或者在线困难样本挖掘（Online hard example mining - OHEM）。

相反，单阶段检测器在处理每张图片时都必须面对一个大得多的候选物体位置集合。在实际操作中，候选位置的个数通常会超过10万，密集地排布在不同的空间位置，比例和宽高比上。同样的采样启发学习也可以应用在单阶段检测器，但是因为训练过程很容易被易分类背景样本（easily classified background examples）影响，所以效率比较低。

此论文因此提出一个新的损失函数，它对于类别不平衡问题更有效。新的损失函数是一个动态比例调节的交叉熵损失函数，当正确类别的置信度上升时，比例因子（scaling factor）退为0，如下图所示。比例因子可以自动地降低训练过程中易样本（easy examples）的影响，而将模型关注在比较难判别的样本上。实验显示，Focal Loss 使我们能够得到一个高精度单阶段的检测器，超过那些需要采样启发学习（sampling heuristics）或难样本挖掘（hard example mining）的双阶段检测器。

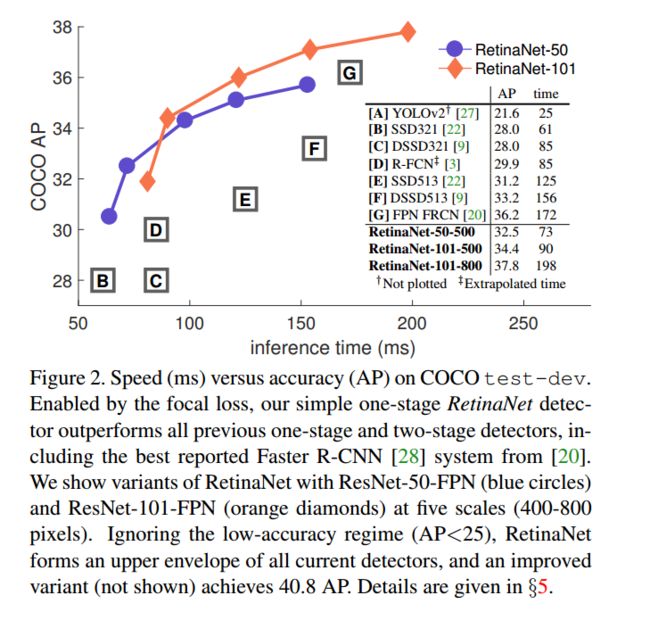
为了证明Focal Loss的有效性，作者设计了一个简单的单阶段目标检测器，叫做RetinaNet（视网膜网络），名字来源于在一幅图片上物体位置的密集采样。它主要包括一个高效的网络内特征金字塔（in-network feature pyramid）和锚点方框（anchor boxes）的使用。RetinaNet高效，高精度。作者基于RestNet-101-FPN网络实现了一个最佳模型，在COCO test-dev AP上获得的准确率为39.1，速度为5FPS，超过了其他发表的单阶段模型和双阶段模型。

2. Related work

Class Imbalance

单阶段检测器（boosted detectors, DPMs, SSD）都在训练中面临着类别不均衡问题。这些检测器在每张图片上要评价1万至10万个候选位置，但只有少部分的侯选位置包含物体。这种不均衡倒置两个问题：（1）在绝大多数的位置，训练是没效率的，因为负样本没有提供任何有用的学习信号；（2）容易负样本（easy negatives）可能破坏训练，使模型退化。一个通常的方案是进行困难样本挖掘（hard examples mining），从训练中提取难分辨的样本。相反，作者展示Focal loss能够自然地解决类别不均衡问题，无需采样就可以在所有样本上高效地训练，也不会发生易样本推翻损失函数和计算梯度。

Robust Estimation

一直以来，人们希望设计一个鲁棒性强的损失函数来消弱异类（outliers, hard examples）的影响，降低高错样本[hard examples]的损失值。但是，Focal Loss 不是去解决异类，而是去降低易样本（inliers, easy examples）的损失值来使得这些易样本对总体损失值的作用变小，因为易样本太多了。所以，Focal loss就是 robust loss的像反面：它着重在一个由困难样本组成的稀疏集合上训练。

3. Focal Loss

Focal Loss 用于解决单阶段目标检测场景任务，在这种场景中前景和背景类别是极其不平衡的（如1：1000）。作者从双类别分类中的交叉熵损失引入Focal loss：
$$CE(p,y)=\{\begin{array}{llccc}-log(p)ify=1& & & & \\ & & & & \\ -log(1-p)otherwise& & & & \end{array}$$
在此函数中，$y\in \{\pm 1\}$表示它是否为ground-truth类，$p\in [0,1]$是对标签$y=1$的类估计出来的概率。为了表示方便，定义了$p_t$:
$$p_t=\{\begin{array}{llccc}pify=1& & & & \\ & & & & \\ 1-potherwise& & & & \end{array}$$
重写$CE(p,y)=CE(p_t)=-log(p_t).$

交叉熵损失函数可被看作图一中上面那根蓝色的曲线。可以看出即便在面对容易区分的样本时（$p_t\ge 0.5$），损失值仍比较大。如果有非常多的容易样本，把它们累加起来，这些小的损失值可能会压垮罕见的类别（如前景类）。

3.1 Balanced Cross Entropy

一个常见的解决类别不平衡的方法是引入一个权值因子（weighting factor）$\alpha \in [0,1]$给类1，$1-\alpha$给类$-1$。在实践中，$\alpha$可被设为类别出现频率的倒数，或被设为一个超参数通过cross validation来调节。为了方便，作者定义${\alpha }_t$，重写基于$\alpha$的CE损失为：
$$CE(p_t)=-{\alpha }_{t}log(p_t).$$

在实验中，作者用基于$\alpha$的交叉熵损失为baseline，和Focal loss作比较。

3.2 Focal Loss Definition

作者的实验证明，训练中密集检测器的大范围的类别不均衡会推翻交叉熵损失。容易分类的负样本贡献了损失中的很大一部分，主导了梯度。尽管$\alpha$平衡了正负（positive/negative）样本的重要性，但是它并没有区分easy/hard 样本。相反，作者提出重构损失函数，来降低容易样本的作用，只关注在训练难负样本（hard negatives）上。

作者提出给交叉熵损失增加一个调节因子（modulating factor）$(1-p_t{)}^{\gamma }$，有一个可调节的焦点参数（focusing parameter）$\gamma \ge 0$。定义此focal loss为：
$$FL(p_t)=-(1-p_t{)}^{\gamma }log(p_t)$$

Focal loss在图一中有可视化展示，$\gamma$有若干个值，$\gamma \in [0,5]$。作者注意到focal loss的两个属性。

（1）当一个样本被错误分类，$p_t$值很小时，调节因子接近1，损失不受影响。当$p_t\to 1$，调节因子趋近0，良好分类的样本损失会被降低。

（2）焦点参数$\gamma$平滑地调节易分样本所产生的影响下降的速率。当$\gamma =0$时，focal loss 和 交叉熵损失等价。随着$\gamma$值上升，调节因子的影响也逐渐上升（作者在实验中发现$\gamma =2$时候结果最优。）

调节因子降低易分样本对损失值的贡献，扩大样本获取低损失的范围。例如，当$\gamma =2$，一个概率是$p_t=0.9$的样本，它的focal loss损失值会比交叉熵损失值低100倍；如果它的概率是$p_t\approx 0.968$，它的损失值会比交叉熵低1000倍。这其实就增加了误分类样本的重要性。

实际操作中，作者使用了一个Focal loss的 $\alpha -$平衡（$\alpha -balanced$）变形：
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }log(p_t)$$

此函数在实验中能比非-$\alpha$-平衡函数些微地提升精度。最终，我们注意到损失层的实现结合了计算$p$的sigmoid操作与损失计算操作，带来更强的数值稳定性。

在主要的实验中，作者基本使用上述的focal loss定义。

3.3 Class imbalance and Model initialization

默认地，二分类模型将初始化输出为等概率的$y=-1$或$y=1$。基于这样的初始化以及类别不均衡性，高频类别的损失会主导总体损失，引起早期训练的不稳定。为了对抗这个问题，在训练一开始，作者就针对罕见类别（rare class, 即前景类）的模型估计概率$p$的值引入了"prior"的概念。作者将prior表示为$\pi$，设好它的值，这样模型对罕见类别样本的估计概率$p$较低，例如0.01。这是对模型初始化的一个改动，不是对损失函数的改动。作者发现，它能在严重类别不均衡的情形中，提升交叉熵和focal loss训练的稳定性。

3.4 Class imbalance and Two-stage detectors

双阶段检测器经常用交叉熵损失函数来训练，不包含$\alpha -balance$或作者提出的focal loss。相反，它们通过两个机制来解决类别不均衡问题：（1）双阶段级联；（2）带偏向的小批量采样（biased minibatch sampling）。第一个级联阶段是一个候选框机制，将选取的候选框位置数量从几近无穷降低到一千或两千个。重要的是，选取的候选框不是随机的，它们对应着真实候选框位置，这就减去了绝大多数容易区分的负样本（easy negative examples）。训练第二个阶段时，带有偏向的采样用于构建小批量（minibatch），里面的正负样本比例是1：3。这个比例值就像是采样阶段中的隐（implicit）$\alpha -balance$因子一样。作者提出的focal loss就是在单阶段检测系统中通过损失函数来实现这个问题。

4. RetinaNet Detector

RetinaNet 是一个简单的，统一的网络结构，由一个backbone网络和两个特殊任务的子网络构成。Backbone网络负责计算整幅图片的一个卷积特征图。第一个子网络在backbone的输出上进行卷积物体分类，第二个子网络进行卷积边界框回归。这两个子网络设计结构简单，是单阶段的密集检测。

Feature pyramid network backbone

作者使用了FPN作为RetinaNet 的 backbone 网络。FPN用从上到下的通路和侧边连接来增强一个标准卷积网络，这样模型能够从单个输入图像中有效地构建出一个丰富的，多比例的特征金字塔。金字塔的每一层都能用于在不同比例上检测物体。FPN在全卷积网络基础上改进了多比例预测。

作者将FPN构建于ResNet结构之上。作者构建一个从$P_3$层到$P_7$层的金字塔，$l$表示金字塔层级（$P_l$的分辨率比输入图低$2^l$倍）。所有的金字塔层级都有$C=256$个通道。作者实验表明，仅使用ResNet中生成的特征会导致平均精度较低。

Anchors

作者使用了RPN的变体中的平移不变（translation-invariant）的anchor方框。这些anchors面积从$P_3$到$P_7$分别为$32^2$到$512^2$。在每个金字塔层级上，作者使用3个不同宽高比$\{1:2,1:1,2:1\}$的anchors. 对于较密集的比例覆盖，在每层原来的3个宽高比的anchors上，有3个大小为$\{2^0,2^{1/3},2^{2/3}\}$的anchors。这提升了平均精度。总之，在每层有$A=9$个anchors，对于网络的输入图片，这些anchors覆盖的范围为$32-813$个像素点。

每个anchor都有一个长度为$K$的分类目标向量，$K$是物体类别的个数，以及一个物体边框的4值向量。作者使用RPN中的判定方法，但是改为了多类别检测，而且阈值可以调节。通过阈值为0.5的 IoU（intersection over union），每个anchor都对应着一个真实目标候选框；如果IoU属于$[0,0.4]$，则它被认为是背景。每个anchor最多对应一个真实物体框，我们把$K$标签向量中它对应的那个元素值设为1，其余的设为0。如果一个anchor没有对应的，它的IoU属于$[0.4,0.5]$，在训练中可以忽略不计它。候选框回归通过每个anchor与anchor对应的真实物体框之间的偏移来计算，如果没有对应则忽略不计。

Classification Subnet

分类子网络对于$A$个anchors中的每个空间位置来预测$K$个类别物体出现的概率。这个子网络是一个小型的全卷积网络(FCN)，连接到每个FPN；子网络的参数在所有的金字塔层中共享。设计很简单，对于一个由金字塔层得到的$C$通道的特征图输入，子网络应用4个$3\times 3$的卷积层，每个层有$C$个滤波器并跟着一个ReLU激活层，最后是一个有$kA$个滤波器的$3\times 3$的卷积层。最终，sigmoid激活函数对每个空间位置产生$K\cdot A$个二分类预测。作者在实验中使用$C=256,A=9$。

与RPN不同，作者的目标分类子网络更深，使用$3\times 3$卷积，与边框回归子网络不共享参数。

Box Regression Subnet

与目标分类子网络平行的有另一个小型的全卷积网络(FCN)，连接到每个金字塔层，对每个anchor box相对于真实边框（如果存在的话）来实现偏移回归。边框回归子网络的设计与分类子网络一致，除了它在每个位置上输出的是$4A$个线性输出。对于空间位置的$A$个anchors, 这4个输出预测每个 anchor 相对于真实边框的相对偏移。作者使用一个与类无关（class-agnostic）的边框回归器，它需要较少的参数，但是效用差不多。目标分类子网络和边框回归子网络使用各自的参数，尽管它们的结构类似。

4.1 Inference and Training

Inference

RetinaNet 是一个简单的全卷积网络，它的 backbone 网络是一个ResNet-FPN，另有一个分类子网络和边框回归子网络。测试阶段就是简单地将一张图片前向传入网络。为了提速，作者在每个FPN层级中，从至多1000个最高得分预测中提取边框预测（检测器置信度阈值为0.05）。从所有层级中获取的最高得分预测再进行合并，用阈值为0.5的非最大抑制（non-maximum suppression）来做最终决定。

Focal Loss

作者使用focal loss来作为分类子网络的损失输出。发现在实验中$\gamma =2$效果最好，RetinaNet对于$\gamma \in [0.5,5]$的鲁棒性都还可以。当用RetinaNet训练时，focal loss 应用在每张图片的所有约10万个anchors上。这与传统的使用启发学习采样（heuristic sampling）或者难样本挖掘（OHEM, SSD）来给每个minibatch 选取一个由anchors组成的小集合（如256个）不同，每张图片总的 focal loss 是所有10万个anchors 产生的focal loss之和，并由赋给真实边框的 anchors （number of assigned anchors）的个数做归一化。作者并不是通过所有的anchors数量来做归一化，因为绝大多数的anchors 都是容易分类的负样本（背景），它们的损失值在 focal loss 中可被忽略不计。最后作者发现，$\alpha$ — 针对罕见类别的权值也有一个固定的范围，但是它和$\gamma$有关系。通常，$\alpha$应该是随着$\gamma$的增加逐渐缓慢地减少（当$\gamma =2$, $\alpha =0.25$最优）。

Initialization

作者利用ResNet-50-FPN 和 ResNet-101-FPN 作为backbone 网络来做实验。基网络ResNet-50 和 ResNet-101在ImageNet1k上进行预训练。所有的卷积层（除了RetinaNet子网络中的最后一个）都以$b=0$和 Gaussian weight fill with $\sigma =0.01$来进行初始化。对于分类子网络中最后一个卷积层，作者将bias 初始化为$b=-log((1-\pi )/\pi )$，$\pi$的意思是，在训练开始时，每个anchor都应以置信度$\sim \pi$被标注为前景类。作者使用$\pi =0.01$在所有的实验中。这种初始化避免了绝大多数的背景anchors 在第一轮迭代中造成损失函数的不稳定。

5. Experiments

Pls read paper for more details.