tensorflow实例(7)--建立多层神经网络
本文将建立多层神经网络的函数,这个函数是一个简单的通用函数,
通过最后的测试,可以建立一些多次方程的模型,并通过matplotlib.pyplot演示模型建立过程中的数据变化情况

如果你对神经网络不太了解可以参考我前面的一些文章,这里列出一些主要的参考
机器学习(1)--神经网络初探
tensorflow实例(2)--机器学习初试
tensorflow实例(6)--机器学习中学习率的实验
通过最后的测试,可以建立一些多次方程的模型,并通过matplotlib.pyplot演示模型建立过程中的数据变化情况
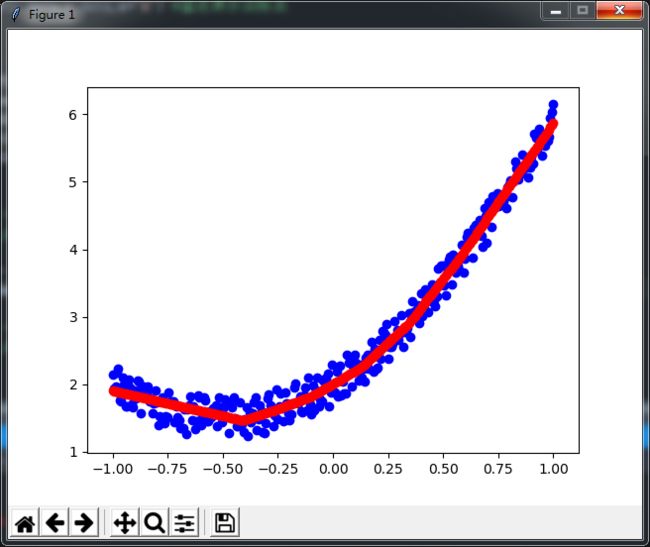
以下三张图片是生成的效果,每张图的蓝点都表示为样本值,红点表示最终预测效果,本例带有点动画效果,可以更直观的觉数值的变化


如果你对神经网络不太了解可以参考我前面的一些文章,这里列出一些主要的参考
机器学习(1)--神经网络初探
tensorflow实例(2)--机器学习初试
tensorflow实例(6)--机器学习中学习率的实验
机器学习(7)--梯度下降法(GradientDescent)的简单实现
#-*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
def createData(ref):
'''生成数据函数,ref 参数说明
本函数将生成一组的x,y数据,ref传参为数组,[a1,a2,a3,b]
x将为一组300个的由-1至1的等分数列组成的数组
y根据ref传参,如上[a1,a2,a3,b],,y = a1*x3次方 + a2*x2次方 + a3*x + b +燥点
'''
x = x_data=np.linspace(-1,1,300).reshape(300,1)
y = np.zeros(300).astype(np.float64).reshape(300,-1)
yStr = ""
for i in range(len(ref)):
y = y + x ** (len(ref) - i - 1) * ref[i]
yStr+= (" = " if yStr == "" else " + ") + str(ref[i]) + " * (" + str(x[3]) + ") ** " + str(len(ref) - i - 1)
noise = max(y) * (np.random.uniform(-0.05,0.05,300)).reshape(300,-1)
y = y + noise
yStr = str(y[3]) + yStr + " + " + str(noise[3][0]) + "(noise)"
print(yStr)
return x,y
def addLayer(inputData,input_size,output_size,activation_function=None):
weight = tf.Variable(tf.random_uniform([input_size,output_size],-1,1))#初始化随机,比全是零要好
b = tf.Variable(tf.random_uniform([output_size],-1,1))#这是来自tensorflow的建议,biases不为零比较较好
mat = tf.matmul(inputData,weight)+b #matul求矩阵乘法并加上biases
if activation_function != None : mat = activation_function(mat)
return mat
def draw(x_data,y_data,trainTimes,learningRate):
'''
trainTimes:训练次数,当次x_data,y_data不同时,trainTimes与learningRate都必须适当调整
关于learningRate这里不在详细说明,可以参考我别的文章
'''
x = tf.placeholder(tf.float32,[None,1])
y = tf.placeholder(tf.float32,[None,1])
#在原始数据x_data与最后预测值之间加上一个20个神经元的神经网络层
#典型的三层网络,N个神级元,x_data,y_data 只有一个属性,算是一个神经元,所以输入是一个神经元,而隐藏层有N个神经元
layer1 = addLayer(x,1,20,activation_function=tf.nn.relu)
prediction = addLayer(layer1,20,1)
loss = tf.reduce_mean(tf.reduce_sum(tf.square(y - prediction),axis=1))
train=tf.train.GradientDescentOptimizer(learningRate).minimize(loss)
sess=tf.Session()
sess.run(tf.initialize_all_variables())
trainStepPrint=int(trainTimes/10)
feed_dict={x:x_data,y:y_data}
predictionStep=[] #用于保存训练过程中的预测结果
for i in range(trainTimes):
sess.run(train,feed_dict=feed_dict)
if i%trainStepPrint==0 or i<10:#分20次将计算的步骤值进行保存,i<10 指最开始的10次,基本前面几次的WEIGHT变化比较大,效果明显
lossVal=sess.run(loss,feed_dict=feed_dict)
print("步骤:%d, loss:%f"%(i,lossVal))
predictionStep.append(sess.run(prediction,{x:x_data}))#预测时并不需要传参y_data
lossVal=sess.run(loss,feed_dict=feed_dict)
print("最后loss:%f"%(lossVal))
predictionStep.append(sess.run(prediction,{x:x_data}))#传入最后结果
sess.close()
plt.scatter(x_data,y_data,c='b') #蓝点表示实际点
plt.ion()
plt.show()
predictionPlt=None
for i in predictionStep:
if predictionPlt!=None:predictionPlt.remove();
predictionPlt=plt.scatter(x_data,i,c='r') #红点表示预测点
plt.pause(0.3)
x_data,y_data = createData([2,0,1])# 2 * x平方 +1 完全的抛物线
draw(x_data,y_data,10000,0.1)
#x_data,y_data = createData([2,2,2])# 2 * x平方 + 2*x + 2 抛物线的一部份,可自行取消注释后运行
#draw(x_data,y_data,10000,0.1)
#x_data,y_data = createData([1,0,2,0]) #3次方的试验,x3次方+ 2*x 可自行取消注释后运行
#draw(x_data,y_data,10000,0.01)