TensorFlow基本操作 实现卷积和池化

之前已经提到过图像卷积的操作和意义，并且用OpenCV中的filter2D函数实现了一些例子。OpenCV中的filter2D函数仅仅是用一个卷积核去卷积单个的图像矩阵，而在TensorFlow中，卷积操作主要用于CNN中的卷积层，所以输入不再仅仅局限与三维或一维的矩阵，卷积核的个数不再是单个，输出的通道数=卷积核的个数，为此TensorFlow提供了tf.nn.conv2d函数实现了一个卷积层的卷积操作。定义如下：

def conv2d(input, 
           filter, 
           strides,
           padding, 
           use_cudnn_on_gpu=None,
           data_format=None, 
           name=None)

其中参数分别为：
第一个参数为当前层的矩阵，在卷积神经网络中它是一个四维的矩阵，即[batch,image.size.height,image.size.width,depth]；
第二个参数为卷积核（滤波器），由tf.get_variable函数创建得到；
第三个参数为不同维度上的步长，其实对应的是第一个参数，虽然它也是四维的，但是第一维和第四维的数一定为1，因为我们不能间隔的选择batch和depth；
第四个参数为边界填充方法。

tf.get_variable函数用以创建卷积核和偏置的权重变量，其结果一般作为tf.nn.conv2d和tf.nn.bias_add函数的输入，函数定义如下：

def get_variable(name,
                 shape=None,
                 dtype=None,
                 initializer=None,
                 regularizer=None,
                 trainable=True,
                 collections=None,
                 caching_device=None,
                 partitioner=None,
                 validate_shape=True,
                 use_resource=None,
                 custom_getter=None)

需要说明的是，其第二个参数表示卷积核的维度，也是一个四维的矩阵，[filter.size,filter.size,depth,num]，前三个参数定义了单个卷积核的尺寸，其中的depth应该等于需要卷积的层的depth，即[batch,image.size,image.size,depth]中的第四个参数。而num可以理解为卷积核的个数，它决定了下一层输出的通道数。

所以在CNN中的一个卷积层的卷积操作在TensorFlow中可以用5行代码来实现——定义卷积核，定义偏置，卷积操作，加入偏置，ReLu激活。

filter_weight = tf.get_variable(name,dtype)
biases = tf.get_variable(name,dtype)
conv = tf.nn.conv2d(input, filter_weight,strides,padding)
bias = tf.nn.bias_add(conv, biases)
actived_conv = tf.cnn.relu(bias)

同样的，TensorFlow也提供了池化操作的函数，其中最大池化为tf.nn.max_pool，平均池化为tf.nn.avg_pool，拿平均池化说吧：

def avg_pool(value, 
            ksize, 
            strides, 
            padding, 
            data_format="NHWC", 
            name=None):

这个函数和tf.nn.conv2d很像，就不逐个参数说明了，主要注意的一定是第二个参数，在tf.nn.conv2d中第二个参数是需要训练权重，而在avg_pool函数中只需要直接给出四个维度就好，这是因为池化操作的卷积核参数不需要训练得到，而是直接指定，参数是什么由是最大池化还是平均池化有关。由于池化操作一般只用来降尺寸，而不是降通道数，所以池化层的核一般选择为[1,2,2,1][1,3,3,1]。

为了更清晰的理解卷积和池化操作，在这里不直接给出网络，而是用指定的卷积核和偏置卷积操作一个指定的矩阵：
假设输入矩阵为：

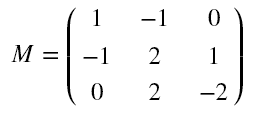
指定卷积核为：

指定偏置为：
[1, 1, 1, …., 1]

import tensorflow as tf
import numpy as np

M = np.array([
        [[1],[-1],[0]],
        [[-1],[2],[1]],
        [[0],[2],[-2]]
    ])
#打印输入矩阵shape
print("Matrix shape is: ",M.shape)
#卷积操作
filter_weight = tf.get_variable('weights',
                                [2, 2, 1, 1], 
                                initializer = tf.constant_initializer([                                                                       [1, -1],                                                                       [0, 2]]))
biases = tf.get_variable('biases', 
                         [1],
                         initializer = tf.constant_initializer(1))
#调整输入矩阵的格式符合TensorFlow的要求，batch=1
M = np.asarray(M, dtype='float32')
M = M.reshape(1, 3, 3, 1)

x = tf.placeholder('float32', [1, None, None, 1])
conv = tf.nn.conv2d(x, filter_weight, strides = [1, 2, 2, 1], padding = 'SAME')
bias = tf.nn.bias_add(conv, biases)
pool = tf.nn.avg_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    #将M feed到定义好的操作中
    convoluted_M = sess.run(bias,feed_dict={x:M})
    pooled_M = sess.run(pool,feed_dict={x:M})

    print("convoluted_M: \n", convoluted_M)
    print("pooled_M: \n", pooled_M)

结果：
Matrix shape is: (3, 3, 1)
convoluted_M:
[[[[ 7.]
[ 1.]]

[[-1.]
[-1.]]]]
pooled_M:
[[[[ 0.25]
[ 0.5 ]]

[[ 1. ]
[-2. ]]]]

在IPython中的结果如上面所示，为了方便换看，把他弄成正常矩阵的形式：
convoluted_M:
[[
[[ 7.] [ 1.]]
[[-1.] [-1.]]
]]
pooled_M:
[[
[[ 0.25] [ 0.5 ]]
[[ 1. ] [-2. ]]
]]
就是上面这样了，需要注意的是，边界填充是在右侧和下方单边填充（补零），即：

（3-2+1）/2+1=2

卷积后加入偏置即为convoluted_M，平均池化后为pooled_M。