《数据分析实战》--用R做多元回归分析

《数据分析实战》——用R做多元回归分析

本文参考的是《数据分析实战》的第六章。

背景：针对某公司对产品的不同广告平台投放，基于过去的新增用户数据和投放数据，希望获得更好的广告投放方式，以此建立数据模型。

现状：不同的广告平台投放，广告效果不同。

预期：对不同的广告平台加以比例，达到最佳效果。

明确问题：通过过去的投放数据和新增用户数据，用多元回归方程来确定不同平台的投放广告比例。

在商业领域，通常的做法是在充分考虑成本的前提下预估一个结果，再采取相应的对策。也就是说，通常我们会先确定结果，再反过来考虑相应对策的成本。放在本次案例中，我们需要先构筑一个可以预估各广告媒体能带来的用户量的模型，再决定广告的投放方式。

线性回归方程思想很简单：我们将数据描绘在图上，每个点表示一个数据，其中横坐标表示的变量称为自变量，纵坐标表示的变量称为因变量。然后我们在图上画出一条与这些数据点最为拟合的直线，根据这条直线上任何一点的横坐标（自变量）的值就可以得到纵坐标（因变量）的值，这就是线性回归分析。

---

读取数据

用R来读取相关数据：

> ad_data <- read.csv('ad_result.csv',header = T,stringsAsFactors = F)
> ad_data
     month  tvcm magazine install
1  2013-01  6358     5955   53948
2  2013-02  8176     6069   57300
3  2013-03  6853     5862   52057
4  2013-04  5271     5247   44044
5  2013-05  6473     6365   54063
6  2013-06  7682     6555   58097
7  2013-07  5666     5546   47407
8  2013-08  6659     6066   53333
9  2013-09  6066     5646   49918
10 2013-10 10090     6545   59963

由于上面的数据已经满足我们对数据分析的需求，故无需做数据处理，直接开始数据分析

---

数据分析

1.首先确认相关性：
首先，我们需要确认广告和新用户数之间是否存在关系。如果二者之间的关系不那么强，就不能断言用户数量的增加是由广告带来的。我们将数据之间的关系的强弱称为“相关性”。为了确认这种相关性，一般来说首先需要观察数据的散点图。

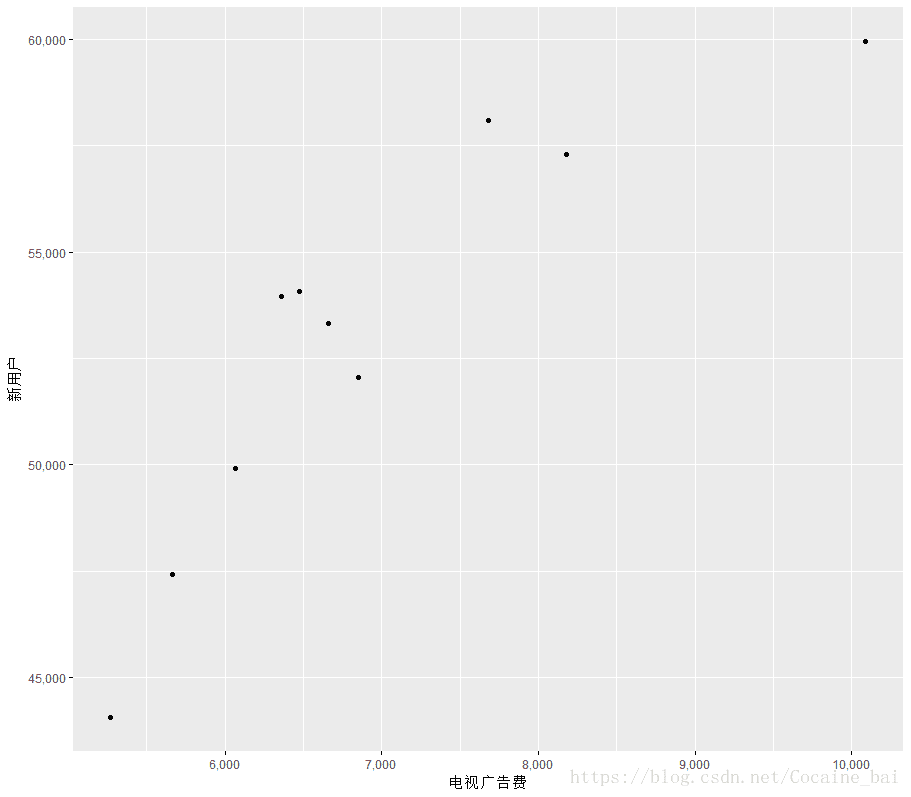
我们先观察tvcm（电视广告费）和install（新用户）之间的散点图：

library(ggplot2)
library(scales)
ggplot(ad_data,aes(x=tvcm,y=install))+
  geom_point()+xlab("电视广告费")+ylab('新用户')+
  scale_x_continuous(labels = comma)+
  scale_y_continuous(labels = comma)

其中，电视广告费和新用户的散点图如下：

我们再观察magazine（杂志广告费）和install（新用户）之间的散点图：

ggplot(ad_data,aes(x=magazine,y=install))+
  geom_point()+xlab("杂志广告费")+ylab('新用户')+
  scale_x_continuous(labels = comma)+
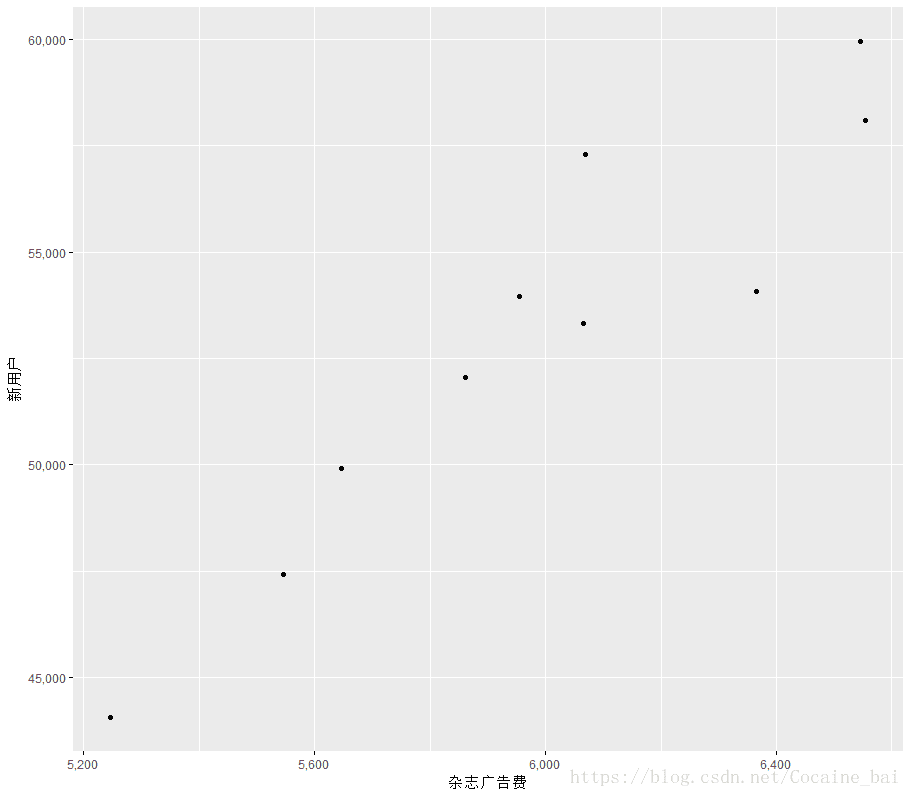
  scale_y_continuous(labels = comma)

其中，杂志广告费和新用户的散点图如下：

可以看出，电视广告和杂志广告分别与新用户的增加有着正相关性，下面我们来确定函数关系

2.进行回归分析
在R语言中，进行回归分析通常使用lm 函数。

lm (A ~ . , data = ZZ[, c(“A”,”B”,”C”)])

首先，通过data= 来指明进行回归分析所需要用到的是ZZ 数据中的属性A、B 和C，并在这之前指明所需要用到的回归模型。
上式中的“A ~ .”表示回归模型为A=B+C。其中“~”相当于数学中的等号，“.”是一个省略记号，表示在data 中声明使用的所有属性里将除属性A 之外的其他所有属性相加。因此上式等同于lm(A~B+C,data=ZZ[, c(“A”,”B”,”C”)])。又因为上式中除属性A 外只有2 个属性，所以不用省略直接列出其他所有属性也是可以的，但当用到的属性数量多达几十个时，使用省略记号“.”还是很方便的。

> fit <- lm(install~.,data=ad_data[,c("install","tvcm","magazine")])
> fit

Call:
lm(formula = install ~ ., data = ad_data[, c("install", "tvcm", 
    "magazine")])

Coefficients:
(Intercept)         tvcm     magazine  
    188.174        1.361        7.250

这里要注意的是：选择列的时候，使用双引号（“”）

通过输入fit 就能确定多元回归方程的系数，从而构建出多元回归模型。例如从上面的结果我们可以得到以下模型。

新用户数= 1.36× 电视广告费+ 7.25× 杂志广告费+ 188.17

Intercept为截距（即常量），另外的两个为系数。

3.对回归分析结果的解释：

> summary(fit)

Call:
lm(formula = install ~ ., data = ad_data[, c("install", "tvcm", 
    "magazine")])

Residuals:
     Min       1Q   Median       3Q      Max 
-1406.87  -984.49   -12.11   432.82  1985.84 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept)  188.1743  7719.1308   0.024  0.98123   
tvcm           1.3609     0.5174   2.630  0.03390 * 
magazine       7.2498     1.6926   4.283  0.00364 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1387 on 7 degrees of freedom
Multiple R-squared:  0.9379,    Adjusted R-squared:  0.9202 
F-statistic: 52.86 on 2 and 7 DF,  p-value: 5.967e-05

① Residuals
残差也就是预测值和实际值之差，我们将残差的分布用四分位数的方式表示出来，就可以据此来判断是否存在较大的偏差。

② Coefficients
这里是与预估的常数项和斜率相关的内容。每行内容都按照预估值、标准误差、t 值、p 值的顺序给出。我们可以由此得知各个属性的斜率是多少，以及是否具有统计学意义。

③ Multiple R-squared、Adjusted R-squared
判定系数越接近于1，表示模型拟合得越好。

结论：
通过观察残差的分布，我们发现1Q（第1 四分位数）的绝对值比3Q（第3 四分位数）的绝对值要大，这表明某些数据的分布偏差过大。但由于自由度校正判定系数的值高达0.92，因此之前所决定的广告策略应该没有什么问题。

所以建立的数据模型是：
新用户数= 1.361× 电视广告费+ 7.250× 杂志广告费+ 188.174

至此，数据分析结束~

---