中文分词和HMM模型

一、中文分词

1.1 切分方案的标识

0有1/意2见3/分4歧5

两种标识方案

1. 一个词的开始位置标识为1，其余位置标识为0，比如：[11010]
2. 切词的索引位置，则“0有1意2见3分4歧5”的分词结点序列{0，1，3，5}

最常见的分词方法是基于词典匹配，规则是按照最大长度查找，由方向的不同可分为两类：前向查找和后向查找（后向查找准确度相对较高）

数据结构

• 为了提高查找效率，不要逐个匹配词典中的词
• 查找词典所占的时间较长，为了保证切分速度，选择一个好的查找词典方法
• Trie树常用于加速分词查找词典问题

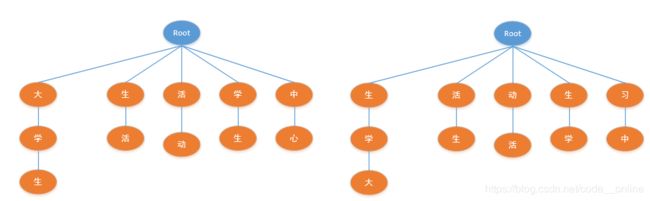
1.2 Trie树

例子：大学生活动中心

• 正向切词：大学生/活动/中心
• 反向切词：大学生/活动/中心

1.3 DAG（有向无环图）

1.4 概率模型

从统计思想的角度来看，分词问题的输入是一个字串$C=c_1.c_2,...,c_n$，输出是一个词串$S=w_1,w_2,...,w_m(n>m)$，对于一个特定的字串，对应着多个切分方案$S$，分词的任务是在这些S中找出一个合适的切分方案，使得$p(S|C)$最大。

$p(S|C)$是字串C产生词串S的概率
$$Seg(C)=arg\underset{SϵG}{\max }p(S|C)=arg\underset{SϵG}{\max }\frac{p(C|S)p(S)}{p(C)}$$

N元模型

• N元模型使用n个词组成的序列来衡量切分方案的合理性
• $p(w_1,w_2,w_3)=p(w_1)p(w_2|w_1)p(w_3|w_1,w_2)$
• $p(S)=p(w_1,w_2,...,w_n)=p(w_1)p(w_2|w_1)p(w_3|w_1,w_2)...p(w_n|w_1,w_2,...,w_{n-1})$

如果一个词的出现不依赖前面出现的词，叫做一元模型
$$p(S)=p(w_1,w_2,...,w_n)=p(w_1)p(w_2)p(w_3)...p(w_n)$$

如果简化为一个词的出现仅依赖于前面出现的一个词，那么称之为二元模型
$$p(S)=p(w_1,w_2,\dots \dots ,w_n)=p(w_1)p(w_2|w_1)p(w_3|w_2)\dots \dots p(w_n|w_{n-1})$$
如果简化为一个词的出现仅依赖于前面出现的两个词，那么称之为三元模型
$$p(S)=p(w_1,w_2,\dots \dots ,w_n)=p(w1)p(w_2|w_1)p(w_3|w_1,w_2)\dots \dots p(w_n|w_{n-2},w_{n-1})$$

1.5 jieba分词

• 支持三种分词模式
  • 精确模式：将句子最精确的分开，适合文本分析
  • 全模式：句子中所有可以成词的词语都扫描出来，速度快，不能解决歧义
  • 搜索引擎模式：在精确模式基础上，对长词再次切分，提高召回
• 支持繁体分词
• 支持自定义字典
• 基于Trie树结构实现高效的词图扫描，生成句子汉字所有可能成词情况构成的有向无环图
• 采用动态规划查找最大概率路径，找出基于词频的最大切分组合
• 对于未登录词，采用了基于汉字成词能力的HMM模型，使用Viterbi算法

中文分词流程

jieba登录词词库加载

jieba的DAG词图

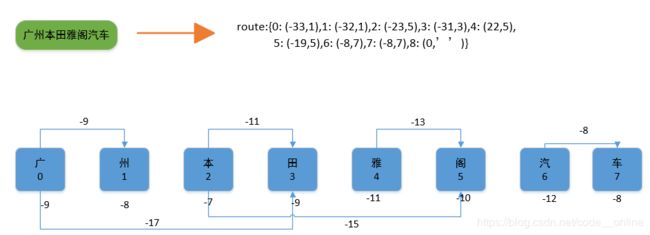
jieba的Route概率-获得词频最大切分

隐马尔可夫模型

• 观察和隐藏序列共同构成隐马尔可夫模型HMM
• $O(o_1,o_2,...,o_T)$：观测序列，$o_t$只依赖于$s_t$
• $S(s_1,s_2,...,s_T)$：状态序列，S是Markov序列，假设1阶Markov序列，则$s_{t+1}$只依赖于$s_t$

二、HMM模型（隐马尔可夫模型）

2.1 马尔可夫模型

定义：每一个状态只依赖于前面有限个状态

• N阶马尔可夫：依赖前面n个状态
• 1阶马尔可夫：仅依赖前一个状态

参数

• 状态，假设有N个
• 初始概率，每一个状态的初始概率${\pi }_k$$${\pi }_k=p(S_1=k)[k=1,2,....N]$$
• 状态转移概率，一个状态转移到另一个状态的概率$[a(k,l)](N\ast N)$$$a_{k,l}=p(S_{t+1}=l|S_t=k)[k,l=1,2,...,N]$$

2.2 隐马尔可夫模型

定义：描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测随机序列的过程。
隐藏的序列称为状态序列；每一个状态数据生成一个观测数据而生成一个观测序列，称为观测序列。

应用：

• 机器翻译：源语言序列->目标语言序列
• 语音识别：语音信号序列->文字序列
• 词性标注：文字序列->词性序列
• 拼音纠错：原始拼音序列->纠正的文字序列

观察序列O的数据通常是由对应的隐藏序列数据决定的，彼此之间相互独立；隐藏序列数据间相互依赖，构成马尔可夫序列

隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。

设Q是所有可能的状态集合，V是所有可能的观测集合$$Q=\{q_1,q_2,...,q_N\},V=\{v_1,v_2,...,v_M\}$$

初始状态概率$${\pi }_i=p(i_1=q_i),i\in (1,2,...,N)$$

A是状态转移概率分布$$A=[a_{ij}{]}_{N\times N}$$$$a_{ij}=p(i_{t+1}=q_j|i_t=q_i),(i,j\in (1,2,...,N))$$

B是观测概率分布$$B=[b_j(k){]}_{N\times M}$$$$b_j(k)=p(o_t=v_k|i_t=q_j)k\in (1,2,...,M);j\in (1,2,..,N)$$

2.3 隐马尔可夫模型的三种计算场景

1. 概率计算问题
   • 给定模型参数λ和观测序列O，计算在模型λ下观测序列O出现的概率
2. 学习问题
   • 已知观测序列O，估计模型参数λ，使得在该模型下观测序列概率P(O|λ)最大，即用极大似然估计的方法估计参数
3. 预测问题
   • 已知模型参数λ和观测序列O，求对给定观测序列条件概率P(S|λ)最大的状态序列S。即给定观测序列，求最优的状态序列。

条件概率的转化$$p(w_2,w_3|w_1)=p(w_2|w_1)p(w_3|w_1,w_2)$$

（1） 概率计算算法

1.1 直接计算法（穷举法）

思想：通过列举所有可能的长度为T的状态序列S，求各个状态序列S与观测序列O的联合概率P(O,S|λ)，然后对所有可能的状态序列求和，得到P(O|λ)。

某一状态序列的概率$$P(S|\lambda )={\pi }_{s_1}{a}_{s_1,s_2}{a}_{s_2,s_3}\cdots a_{s_t-1,s_t}$$

观察序列和对应的隐藏序列的联合概率为$$\begin{array}{rl}P(O_{1:t},S_{1:t}|\lambda )& =P(S_{1:t}|\lambda )P(O_{1:t}|S_{1:t},\lambda )\\ & ={\pi }_{s_1}{a}_{s_1,s_2}{a}_{s_2,s_3}\cdots a_{s_{t-1}:s_t}{b}_{s_1}(o_1)b_{s_2}(o_2)\cdots b_{s_t}(o_t)\\ & ={\pi }_{s_1}\prod _{i=1}^{t-1}{a}_{s_i,s_{i+1}}\prod _{i=1}^t{b}_{s_i}(o_i)\end{array}$$

复杂度为$O(T\ast N^T)$

1.2 前向概率

给定隐马尔可夫模型参数$\lambda$，定义到时刻t的部分观测序列为$o_1,o_2,...,o_t$且对应的隐藏状态为$k$的概率为前向概率。

$$\begin{array}{rl}{\alpha }_t(k)& =p(O_{1:t},S_t=k|\lambda )\\ & =\sum _{l=1}^{N}p(O_{1:t},S_{t-1}=l,S_t=k|\lambda )\\ & =\sum _{l=1}^{N}p(O_t|O_{1:t-1},S_{t-1}=l,S_t=k,\lambda )p(O_{1:t-1},S_{t-1}=l,S_t=k|\lambda )\\ & =\sum _{l=1}^{N}p(O_t|O_{1:t-1},S_{t-1}=l,S_t=k,\lambda )p(S_t=k|O_{1:t-1},S_{t-1}=l,\lambda )p(O_{1:t-1},S_{t-1}=l|\lambda )\\ & =\sum _{l=1}^{N}p(O_t|S_t=k,\lambda )p(S_t=k|S_{t-1}=l,\lambda )p(O_{1:t-1},S_{t-1}=l,\lambda )\\ & =\sum _{l=1}^N{b}_k(O_t)a_{l,k}{\alpha }_{t-1}(l)\end{array}$$
前向概率公式表示$p(O|\lambda )$$$p(O|\lambda )=\sum _{l=1}^N{\alpha }_T(l)$$

$p(O|\lambda )$的时间复杂度为$O(T\ast N^2)$

1.3 后向概率

给定隐马尔可夫模型$\lambda$，定义在t时刻状态为$k$的条件下，从$t+1$到$T$的部分观测序列为$O_{t+1},O_{t+2},...,O_T$的概率为后向概率。
$$\begin{array}{rl}{\beta }_t(k)& =p(O_{t+1,T}|S_t=k,\lambda )\\ & =\sum _{l=1}^{N}p(O_{t+1:T},S_{t+1}=l|S_t=k,\lambda )\\ & =\sum _{l=1}^{N}p(S_{t+1}=l|S_t=k,\lambda )p(O_{t+1:T}|S_{t+1}=l,S_t=k,\lambda )\\ & =\sum _{l=1}^{N}p(S_{t+1}=l|S_t=k,\lambda )p(O_{t+1:T}|S_{t+1}=l,\lambda )\\ & =\sum _{l=1}^{N}p(S_{t+1}=l|S_t=k,\lambda )p(O_{t+2:T}|S_{t+1}=l,\lambda )p(O_{t+1}|O_{t+2:T},S_{t+1}=l,\lambda )\\ & =\sum _{l=1}^{N}p(S_{t+1}=l|S_t=k,\lambda )p(O_{t+1}|S_{t+1}=l,\lambda )p(O_{t+2:T}|S_{t+1}=l,\lambda )\\ & =\sum _{l=1}^N{a}_{k,l}{b}_l(O_{t+1}){\beta }_{t+1}(l)\end{array}$$

后向概率表示$p(O|\lambda )$$$p(O|\lambda )=\sum _{l=1}^N{\pi }_l{b}_l(O_1){\beta }_1(l)$$

前向概率和后向概率表示观测序列概率$$p(O|\lambda )=\sum _{i=1}^N\sum _{j=1}^N{\alpha }_t(i)a_{ij}{b}_j(O_{t+1}){\beta }_{t+1}(j)$$

概率计算

(1) 给定模型$\lambda$和观测序列$O$，在时刻$t$的状态为$k$的概率
$${\gamma }_t(k)=p(S_t=k|O_{1:T},\lambda )=\frac{p(O_{1:T},S_t=k,\lambda )}{p(O_{1:T},\lambda )}=\frac{{\alpha }_t(k){\beta }_t(k)}{{\sum }_{l=1}^N{\alpha }_t(l){\beta }_t(l)}$$

(2) 给定模型$\lambda$和观测序列$O$，在时刻$t$的状态为$i$，时刻$t+1$状态为$j$的概率$$\begin{array}{rl}{\xi }_t(i,j)& =p(S_t=i,S_{t+1}=j|O,\lambda )\\ & =\frac{p(S_t=i,S_{t+1}=j,O|\lambda )}{p(O|\lambda )}\\ & =\frac{p(S_t=i,S_{t+1}=j,O|\lambda )}{{\sum }_{m=1}^N{\sum }_{n=1}^{N}p(S_t=m,S_{t+1}=n,O|\lambda )}\\ & =\frac{{\alpha }_t(i)a_{i,j}{b}_j(O_{t+1}){\beta }_t(j)}{{\sum }_{m=1}^N{\sum }_{n=1}^N{\alpha }_t(m)a_{m,n}{b}_n(O_{t+1}){\beta }_t(n)}\end{array}$$

（2） 学习算法

监督学习方法（完全数据）

假设已给训练数据包含了观测序列O和对应的状态序列S，利用极大似然估计方法来估计隐马尔可夫模型的参数

非监督学习方法（不完全数据）

假设给定训练数据只包含了$S$个长度为$T$的观测序列$O$，而没有对应的状态序列，目标是学习隐马尔可夫模型参数$\lambda =(A,B,\pi )$

（3） 预测算法

维特比算法：动态规划求概率最大路径，这时一条路径对应着一个最优的状态序列。过程是从时刻t=1开始，递推地计算在时刻t状态为i的各条部分路径的最大概率，直至得到时刻t=T状态的各条路径的最大概率。时刻T的最大概率即为最优路径的概率P，得到最优路径的终结点。之后，为了找出最优路径的各个结点，从终结点开始，由后向前逐步求结点，从而得到最优状态序列。

每一个字所对应四种状态（BMES），status_matrix记录k的四种状态到j的某种状态（pi+A+B）的概率最大值，数据结构为【max_p,max_status】(BMES),直到最后一个字。从最后一个字的四种状态查询概率最大值，回溯搜索前一个字的最优状态，从而得到最优序列。

动态规划在t+1的位置重用t的结果。
变量δ定义了在时刻t状态为k的所有路径$O_{1:t}$中概率最大值为
$$\begin{array}{rl}{\delta }_t(k)& =\underset{S_{1:t-1}}{\max }p(S_{1:t-1},S_t=k,O_{1:t}|\lambda ){\delta }_{t+1}(k)=\underset{S_{1:t}}{\max }p(S_{1:t},S_{t+1}=k,O_{1:t+1}|\lambda )\\ & =\underset{1\le l\le M}{\max }(\underset{S_{1:t-1}}{\max }p(S_{1:t-1},S_t=l,S_{t+1}=k,O_{1:t+1}|\lambda ))\\ & =\underset{1\le l\le M}{\max }(\underset{S_{1:t-1}}{\max }p(S_{t+1}=k,O_{t+1}|S_{1:t-1},S_t=l,O_{1:t},\lambda )p(S_{1:t-1},S_t=l,O_{1:t}|\lambda ))\\ & =\underset{1\le l\le M}{\max }(\underset{S_{1:t-1}}{\max }p(S_{t+1}=k,O_{t+1}|S_t=l,\lambda )p(S_{1:t-1},S_t=l,O_{1:t}|\lambda ))\\ & =\underset{1\le l\le M}{\max }(\underset{S_{1:t-1}}{\max }p(S_{t+1}=k|S_t=l,\lambda )p(O_{t+1}|S_{t+1}=k,\lambda )p(S_{1:t-1},S_t=l,O_{1:t}|\lambda ))\\ & =\underset{1\le l\le M}{\max }{a}_{l,k}{b}_k(O_{t+1}){\delta }_t(l)\end{array}$$

ψ定义了时刻t状态为k的所有路径中概率最大的路径的第t-1个结点为
$${\psi }_t(k)=arg\underset{1\le l\le M}{\max }[{\delta }_{t-1}(l)a_{l,k}]$$

三、中文切词实践

结巴切词

jieba切词

import jieba

str = "中国第十九届人工智能机器学习会议将在重庆举办,举办的内容主要包括大数据云计算多粒度粗糙集"

print("/".join(jieba.cut(str,cut_all=False)))

结果显示：一些专有名词被切开（词典没有这些专有名词）

加载自定义词典

自定义词典user_dict.txt

中文分词
大数据
云计算
机器学习
多粒度

import jieba

def_dict = "user_dict.txt"  #自定义词典路径
jieba.load_userdict(def_dict)   # 加载外部的词典

str = "中国第十九届人工智能机器学习会议将在重庆举办,举办的内容主要包括大数据云计算多粒度粗糙集"

print("/".join(jieba.cut(str,cut_all=False)))

结果显示：这些专有名词作为一个词被切割（外部词典加载到默认词典）

新词发现

import jieba
from sklearn.feature_extraction.text import CountVectorizer

# 新词发现
s_list = ['中文分词中文计算','大数据中国好声音','云计算中国好声音','用结巴分词来做中文分词','云计算大数据']
s_l = [' '.join(jieba.cut(x)) for x in s_list]

# ngram_range : tuple (min_n, max_n)表示合并词的数量范围 如【人工 [智能】 机器]
# min_df : float in range [0.0, 1.0] or int, default=1表示为词频的最小值，筛选出大于这个值的组合词
# token_pattern表示切分词后的模式
ngram_vec = CountVectorizer(token_pattern=r'\b\w+\b',ngram_range=(2,2),min_df=0.4)
x1 = ngram_vec.fit_transform(s_l) # 训练模型
print(x1)
print(ngram_vec.vocabulary_)
# 新词格式化
new_word = dict()
for k,v in ngram_vec.vocabulary_.items():
    new_word[k.replace(' ','')] = v
print(new_word)

输出结果发现新词，然后加载到词典用于jieba切词

参考文献

• 李航 《统计学习方法》