浅析拯救小矮人的 nlogn 算法及其证明
题型简介:
有 $ n $ 个人,第 $ i $ 个人身高 $ a_i $ 手长 $ b_i $ ,他们为了从一个高为 $ H $ 的洞中出去,决定搭人梯。如果一个人和他下面的人的身高之和加上他的手长可以达到洞的高度,那么他就可以出去。求最多有多少人能出去。 $ n\leq 10^6 $
算法流程
本题需要贪心,所以我们可以贪心到底。首先我们将所有人,按照他们的最低逃生高度 $ H-a_i-b_i $ 从高到低排序。一个必须要知道的结论:最低逃生高度越高的人,一定越先走。
首先我们将所有人按照 $ H-a_i-b_i $ (最低逃生高度)从高到低排序,根据结论越高的人越先走。然后如果是 $ n^2 $ 背包,就是对每个人做有条件的背包,模拟每个人是否能走。
而 $ n\times logn $ 的方法则是记录一个后缀 $ s[] $ ,其中 $ s[i] $ 表示第 $ i $ 个人后面最低逃生高度比他低的所有人的身高总和,然后用一个 $ tot $ 记录前面没有出去的人的身高总和,对于从高到低枚举的第 $ i $ 个人,如果 $ s[i]+tot>=H-a_i-b_i $ 就说明他能出去(于是默认他出去);否则就将这个人的身高和前面所有已经出去的人的身高作比较,如果当前这个人最高那么他就不出去了,不然就从前面已经出去的人里面找到那个最高的人,把他拉回洞里垫在下面,让当前这个人出去!照着这个过程做我们就能得到最优解。
算法证明:
其实这个算法只有两个待考究的地方,问题一:为什么最低逃生高度高的人,一定越先走?这个问题在很多题解里已经讨论过了,难以讲清,本题不做多讲,就用一张图感性一下:
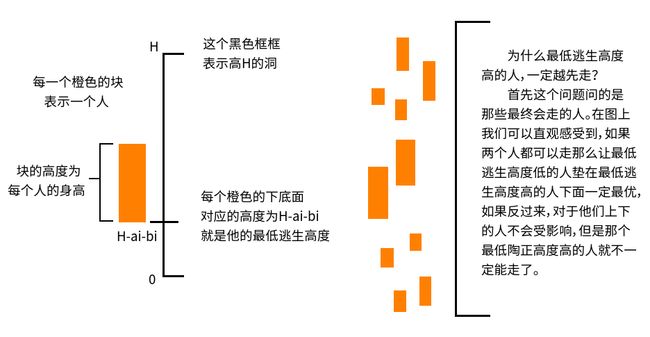
本算法第二个问题在于这句话: 否则就将这个人的身高和前面所有已经出去的人的身高作比较,如果当前这个人最高那么他就不出去了,垫到下面去;不然就从前面已经出去的人里面找到那个最高的人,把他拉回洞里垫在下面,让当前这个人出去!为什么把上面最高的那个人拉下来,这个人就一定可以出去了?为什么只取一个人下来,我们可不可以拉多个人下来,让当前这个人出去的同时为后面的人垫高度?这个我们用两张图解读:
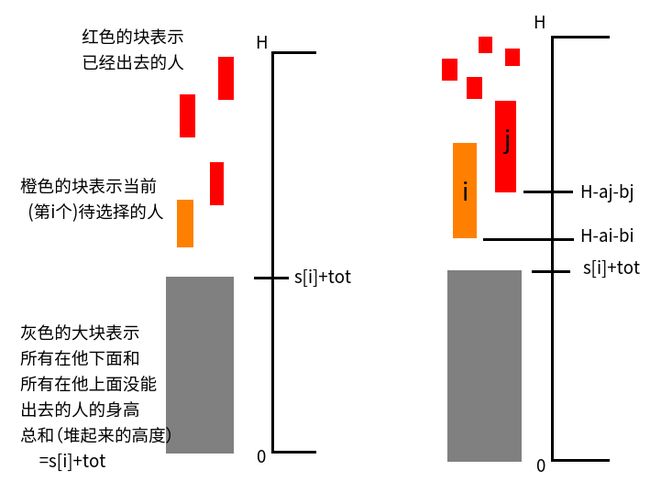

$ code: $
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include


