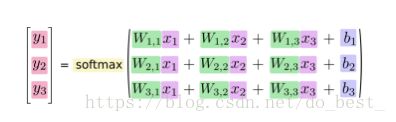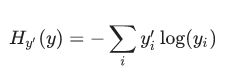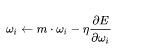深度学习算法及其应用

一、实验目的

二、实验的硬件、软件平台

三、实验内容和步骤

四、思考题

五、实验心得与体会

 

一、实验目的

 

1、了解深度学习的基本原理，能够解释深度学习原理；

2、能够使用深度学习开源工具tensorflow识别图像中的数字，对实验性能进行分析；

3、了解图像识别的基本原理。

 

二、实验的硬件、软件平台

 

硬件：计算机

软件：操作系统：WINDOWS2000

应用软件：Tensorflow，Python，NumPy, SciPy, iPython 

 

三、实验内容和步骤

【深度学习】

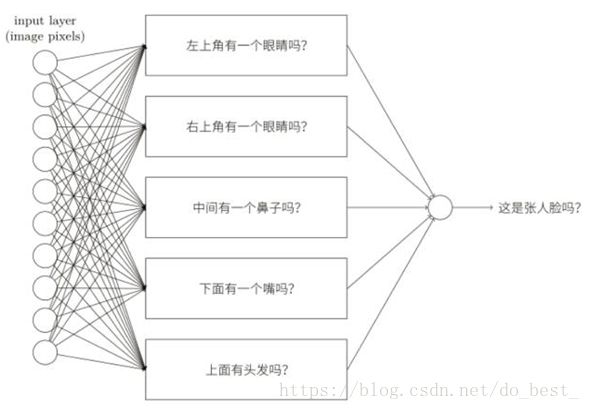
机器学习中一种基于对数据进行表征学习的方法。其动机在于建立、模拟人脑进行分析学习的神经网络，它模仿人脑的机制来解释数据，例如图像，声音和文本。 通过组合低层特征形成更加抽象的高层表示属性类别或特征，以发现数据的分布式特征表示，含多隐层的多层感知器就是一种深度学习结构。深度学习的好处是用非监督式或半监督式的特征学习和分层特征提取高效算法来替代手工获取特征。

【将MNIST二进制数据集转化为图片形式】

 

实验要求每个人数据集不相同，所以从下载的MNIST数据集中利用随机函数随机选择其中的一部分数据进行训练、测试。

准备数据：

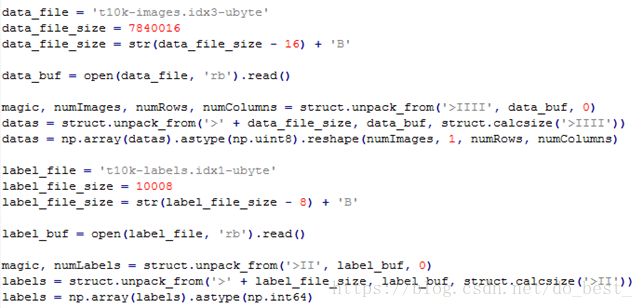
在TensorFlow中为了获取这个数据MNIST Data，封装了一个方法，我们调用这个方法，程序就会自动去下载和获取数据集。代码如下：

// 导入input_data这个类
from tensorflow.examples.tutorials.mnist import input_data
//从这个类里调用read_data_sets这个方法
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

获取到的数据集有3部分组成： 
（1）55,000个训练样本（用来训练模型） 
（2）10,000个测试样本（用来测试模型，避免过拟合） 
（3）5,000个验证样本（用来验证超参数） 
(一般在机器学习的建模中，都需要准备这3类数据集。)

对于每一个样本点，有两部分数据组成： 
（1）手写数字图片，记做x 
（2）标签，记做y

转化训练集数据：

转化测试集数据：

保存之后如下图所示（以3为例）：

其中，手写数字图片由28*28像素组成，可以将其转换成28*28的由数字组成的数组。如下例子：

而这个28*28的数组又可以铺平成1*784的一个向量。运行以上两行代码下载数据，直接调用mnist.train.images，获取训练数据集的图片， 这是一个大小为[55000, 784]的tensor，第一维是55000张图片，第二维是784个像素。像素的强度是用0-1之间的数字表示的。 

根据需要，我们需要将这0-9的数字标签转换成one-hot编码，比如原来的标签是3，编码之后就变成了[0,0,0,1,0,0,0,0,0,0],也就是生成一个1*10的向量，分别对应0-9的数字在3对应的位置上为1，其余位置上都是0. 经过这样编码之后，训练集的标签数据就变成了[55000,10]的浮点类型的数组了。

【建立多分类模型】

 

Softmax Regressions原理

因为我们的目的是区分出0-9的数字，也就是要将图片在这10个类中进行分类，属于多元分类模型。对于一张图片，我们想要模型得到的是属于这10个类别的概率，举个例子，如果模型判断一张图片属于9的概率由80%，属于8的概率是5%，属于其他数字的概率都很小，那么最后这张图片应被归于9的类别。SoftmaxRegressions是一个非常经典的用于多分类模型的方法。

Softmax Regressions主要有2步：

1、分别将输入数据属于某个类别的证据相加；

2、将这个证据转换成概率。

证据：线性模型，由权重w，与偏执项b组成：

 

i表示第i类，j表示输入的这张图片的第j个像素，也就是求将每个像素乘以它的权重w，在加上偏执项的和。

求出了evidence之后，就要使用softmax函数将它转换成概率了。 

 

这里的softmax其实相当于是一个激活函数或者连接函数，将输出的结果转换成我们想要的那种形式（在这里，是转换成10各类别上的概率分布）。那么这个softmax的过程是经过了什么样的函数转换呢？如下公式：

展开以上公式：

 

也就是说，将刚刚的线性输出evidence作为softmax函数里的输入x，先进过一个幂函数，然后做正态化，使得所有的概率相加等于1。

将softmaxregression的过程画出来如下： 

如果写成公式，如下：

更直观一些，就是：

【深度神经网络实现图像识别】

 

1）使用tensorflow，实现导入tensorflow的库

Import tensorflowas tf

 

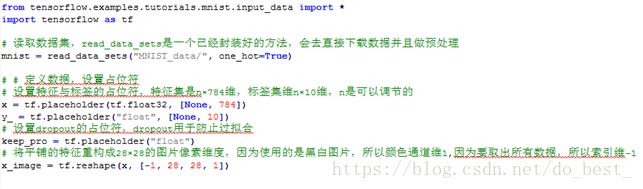
2）为输入数据x创建占位符

x =tf.placeholder(tf.float32, [None, 784])

这里的x并不是具体的数值，而是一个占位符，就是先给要输入的数据霸占一个位置，等当真的让TensorFlow运行计算的时候，再传入x的真实数据。因为我们的输入数据n个是1*784的向量，可以表示成2层的tensor,大小是[None,784],None表示到时候后传输的数据可以任何长度，也就是说可以是任何数量的样本点。

 

3）创建两个权重变量

W和b是在训练过程中不断改变不断优化的，使用variable来创建：

W =tf.Variable(tf.zeros([784, 10]))

b =tf.Variable(tf.zeros([10]))

以上，我们初始化两个权重都为0，在之后的训练与学习中会不断被优化成其他值。注意，w的大小是[784,10]表示784个像素输入点乘以10维的向量（10个类别）。b的大小是[ 10 ]。

 

4）建立损失函数

训练模型的目的是让模型在学习样本的过程中不断地优化参数，使得模型的表现最好。在机器学习中，我们一般使用损失函数来评价模型的好坏。如果模型预测的结果与真实的结果相差越远，那么损失大，模型的表现就越不好。因此，我们渴望去最小化损失从而得到最优的模型。

这里介绍一个最常用的损失函数：交叉熵损失。公式如下：

 

y表示模型预测出来的概率分布，y’表示真实的类别概率分布（就是之间one-hot编码之后的标签）。yi表示预测为第i个类的概率， yi’表示真实属于i类的概率（只有i类为1，其余为0）

交叉熵从一定意义上可以度量模型对于真实情况的拟合程度，交叉熵越大，则模型越不拟合，表现力越差。

要实现交叉熵函数，代码如下：

// 为真实的标签添加占位符
y_ = tf.placeholder(tf.float32, [None, 10])

// 创建交叉熵函数
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

解释一下上面的代码，tf.log表示将y的每一个元素都做log运算；然后将其乘以对应的真实标签的类别y_中的元素。tf.reduce_sum表示的是将索引为1的值进行求和。tf.reduce_mean表示对所有样本的交叉熵求均值。

注意注意，在源码中，我们没有使用这个公式，因为这样计算下去数值不稳定。取而代之的是直接在线性函数之后应用了tf.nn.softmax_cross_entropy_with_gogits（即，没有单独经过softmax函数），这样会更加稳定。

 

5）使用BP算法优化参数

损失函数就是我们的目标函数，要找到目标函数的最小值，就是对参数求偏导等于0.我们可以使用优化器去不断地降低损失寻找最优参数。比如说最常用的是梯度下降法。代码如下：

train_step =tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

上面使用了梯度下降法最小化交叉熵损失，学习率设置为0.5，每一次迭代，w,b两类参数都会改变，直到损失达到最小的时候，就获得了最优的w,b。

 

6）建立softmax模型

y =tf.nn.softmax(tf.matmul(x, W) + b)

以上代码可见，我们先将x与W相乘了，然后加上了b，然后将线性输出经过softmax的转换。

 

7）运行迭代

模型训练的graph基本已经完成，现在我们可以初始化变量，创建会话，来进行循环训练了。

 

在每次循环中，都会从训练集中获取一批样本，每批有100个样本。然后运行train_step这个操作，并且给之前的占位符注入数据。

 

8）模型评估

通过模型的训练，我们得到了最优的参数，但是在这个最优的参数下，模型的表现力可以通过查看在测试集上模型预测的label与样本真实的Label相同的有多少比例。 tf.argmax返回的是一个tensor里在某个维度上最大值的索引，比如tf.argmax(y,1)取出的是预测输出的10个类别的概率向量中最大概率的那个索引（对应某个类别），tf.argmax(y_,1)取出的是该样本的真实类别的索引，如果对于一个样本，两者相同，则说明对该样本的预测正确。下面代码，用tf.equal返回的是一个布尔类型的列表。

要求出正确率，只要将布尔类型的列表全部求和再求均值即可：

现在我们注入数据，来运行测试集上的准确率：

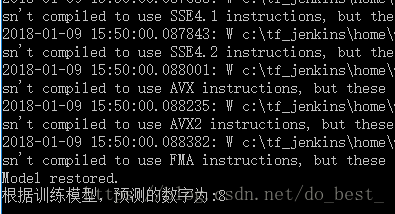
在终端打开命令行，输入python main.py。输出结果如下图：

【卷积神经网络CNN实现图像识别】

        卷积神经网络与普通神经网络的区别在于，卷积神经网络包含了一个由卷积层和子采样层构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连接。在CNN的一个卷积层中，通常包含若干个特征平面(featureMap)，每个特征平面由一些矩形排列的的神经元组成，同一特征平面的神经元共享权值，这里共享的权值就是卷积核。卷积核一般以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。共享权值（卷积核）带来的直接好处是减少网络各层之间的连接，同时又降低了过拟合的风险。子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。

        卷积神经网络由三部分构成。第一部分是输入层。第二部分由n个卷积层和池化层的组合组成。第三部分由一个全连结的多层感知机分类器构成。

卷积层

 

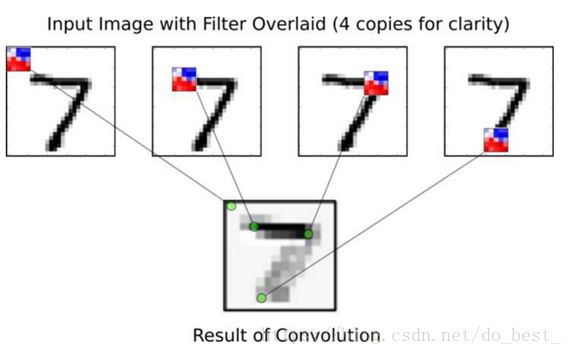
下面的图片展示了在第一个卷积层中处理图像的基本思想。输入图片描绘了数字7，这里显示了它的四张拷贝，我们可以很清晰的看到滤波器是如何在图像的不同位置移动。在滤波器的每个位置上，计算滤波器以及滤波器下方图像像素的点乘，得到输出图像的一个像素。因此，在整张输入图像上移动时，会有一张新的图像生成。红色的滤波权重表示滤波器对输入图的黑色像素有正响应，蓝色的代表有负响应。

在这个例子中，很明显这个滤波器识别数字7的水平线段，在输出图中可以看到它对线段的强烈响应。

 

滤波器遍历输入图的移动步长称为stride。在水平和竖直方向各有一个stride。两个方向的stride都设为1，这说明滤波器从输入图像的左上角开始，下一步移动到右边1个像素去。当滤波器到达图像的右边时，它会返回最左边，然后向下移动1个像素。持续这个过程，直到滤波器到达输入图像的右下角，同时，也生成了整张输出图片。当滤波器到达输入图的右端或底部时，它会用零（白色像素）来填充。因为输出图要和输入图一样大。此外，卷积层的输出可能会传递给修正线性单元（ReLU），它用来保证输出是正值，将负值置为零。输出还会用最大池化(max-pooling)进行降采样，它使用了2x2的小窗口，只保留像素中的最大值。这让输入图分辨率减小一半，比如从28x28到14x14。

 

卷积操作

图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上，所以对于这个图像上的所有位置，我们都能使用同样的学习特征。更直观一些，当从一个大尺寸图像中随机选取一小块，比如说 8x8 作为样本，并且从这个小块样本中学习到了一些特征，这时我们可以把从这个 8x8 样本中学习到的特征作为探测器，应用到这个图像的任意地方中去。特别是，我们可以用从 8x8 样本中所学习到的特征跟原本的大尺寸图像作卷积，从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。

 

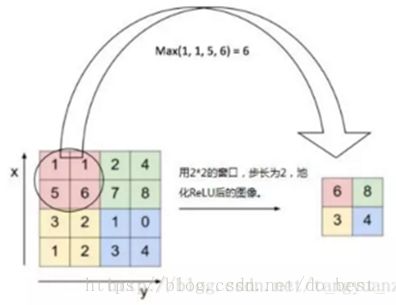
池化层

 

在通过卷积获得了特征 (features) 之后，下一步我们希望利用这些特征去做分类。图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征)，同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling)，有时也称为平均池化或者最大池化 (取决于计算池化的方法)。如下图所示：

 

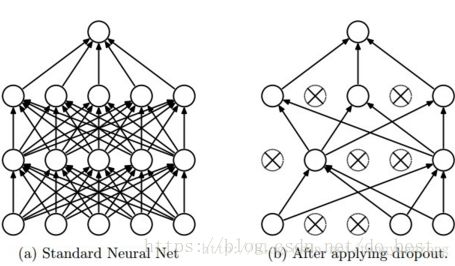
Dropout层

 

dropout是一种防止模型过拟合的技术，这项技术也很简单，但是很实用。它的基本思想是在训练的时候随机的dropout(丢弃)一些神经元的激活，它不会太依赖某些局部的特征（因为局部特征有可能被丢弃）

 

上图a是标准的一个全连接的神经网络，b是对a应用了dropout的结果，它会以一定的概率(dropout probability)随机的丢弃掉一些神经元。

 

全连接层

 

通俗的说就是前面一层的每个单元都与后面一层的相连接。将多次卷积和池化后的图像展开进行全连接，

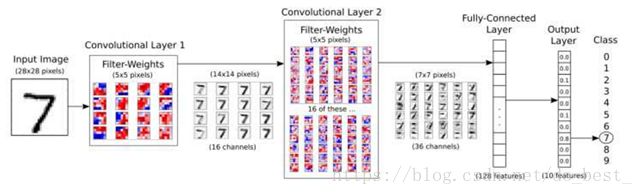
多层卷积神经网络

将卷积操作，ReLU操作，Pooling操作结合起来，我们可以得到如下深度网络，可以看出共进行了2次卷积和池化，完成对输入的图像的特征提取，接下来就是全连接层，经过全连接层，会使用前一层提取的所有主要特征，使用一般的均值方差作为损失函数，在输出层可以使用softmax分类器完成多分类任务。

 

结构改进

 

在实际应用中，我们可以在两层全连接层中添加一个Dropout层来防止模型过拟合。

【具体实现】

 

数据准备

1）导入tensorflow包

2）下载数据

3）创建会话

4）为输入的样本特征x与标签y建立占位符

 

初始化参数的方法封装

 

参数在训练中是会不断变更与优化的，所以为参数创建一组变量。因为在神经网络中每层都会有参数，一个一个去创建显然不科学，最好的方式是写一个function去封装创建参数变量的过程。在神经网络里涉及的参数仍然是2类：w,b.

以上代码中，tf.truncated_normal函数使得w呈正太分布， stddev设置标准差为0.1。也就是说输入形状大小shape，输出标准差为0.1的正太分布的随机参数作为权重变量矩阵。对于参数b，使用了tf.constant()来创建一组指定大小的常数，常数值为0.1。在方法def中都分别初始化了这两个参数。

 

卷积层与池化层的方法封装

 

Tensorflow也在卷积层与池化层给了很多灵活的操作。卷积层与池化层都需要设置一些超参数，比如步长，窗口大小，补全的边界等。在这里选择使用步长为1，用0补全边界，故卷积层的输出与输入的数据大小是一致的。在池化层中，使用2*2的窗口选取窗口中的最大值作为输出。

同样，一个神经网络会有很多个卷积层与池化层，我们不可能去一层一层写，为了使代码更简洁，最好将卷积层与池化层的创建封装成两个方法。如下：

 

第一组卷积层与池化层

这层卷积层总共设置32个神经元，也就是有32个卷积核去分别关注32个特征。窗口的大小是5×5,所以指向每个卷积层的权重也是5×5,因为图片是黑白色的，只有一个颜色通道，所以总共只有1个面，故每个卷积核都对应一组5*5 * 1的权重。因此w权重的tensor大小应是[5,5,1,32] ，b权重的tensor大小应是[ 32 ] ，初始化这两个权重：

在CNN中，我们需要将其组合成28 * 28，因为只有一个颜色通道，确切的来说应该是28 * 28 * 1的数组，-1表示取出所有的数据。

将权重w与样本特征x放进卷积层函数中做卷积运算，然后加上偏置项b。将线性输出进入relu激活函数，激活函数的输出就是卷积层的最终输出，输出tensor的大小仍然是28*28

卷积层的输出就是接下去池化层的输入,池化层的窗口大小为2*2，故输入的28*28，就变成了输出的14*14大小。

 

第二组卷积层与池化层（类似于第一组）

第二层卷积层中，窗口大小仍然是5 * 5， 神经元的个数是64，因为上一层的神经元个数是32，所以这一次的参数w的大小是[5,5,32,64]，参数b的大小是[ 64 ]

经过卷积层tensor的大小是14 * 14,经过池化层tensor的大小变成了7 * 7

 

创建全连接层

 

在经过一组一组的卷积+池化层之后往往会以一个全连接层结尾.，在全连接层设置1024个神经元，图像目前图像数据的大小是 7 * 7,对于全连接层来说需要将图像数据再次铺平成1 * 49的向量，因为上一层有64个神经元，故铺平之后是 7 * 7 * 64 大小的向量。

为了避免过拟合，这里在全连接层使用dropout方法，就是随机地关闭掉一些神经元使模型不要与原始数据拟合得那么准确。

keep_prob表示保留不关闭的神经元的比例。

 

创建输出层：softmax层

 

因为是多分类模型，在全连接后面再添加一层softmax层~，总共类别是10，故最后一层为10个神经元

 

训练与评估模型

 

因此现在我们要按照上面创建好的模型来训练，并且评估这个模型预测的好坏。

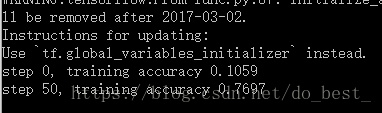
2000次循环，每循环100次，会打印出训练集的误差，打印结果如下：

 

可以看到，随着训练次数的增加，正确率也在不断地增加，当训练次数足够多时，可达99%以上。

 

目前为止，我们利用随机生成的数据集进行了训练和测试，现在我们测试程序是否能识别出我们自己输入的图片中的数字，比如：

【载入图片测试具体步骤】

 

将图片载入到文件目录下，然后进行测试：

（1）载入我的手写数字的图像。

（2）将图像转换为黑白（模式“L”）

（3）确定原始图像的尺寸是最大的

（4）调整图像的大小，使得最大尺寸（醚的高度及宽度）为20像素，并且以相同的比例最小化尺寸刻度。

（5）锐化图像。这会极大地强化结果。

（6）把图像粘贴在28×28像素的白色画布上。在最大的尺寸上从顶部或侧面居中图像4个像素。最大尺寸始终是20个像素和4 + 20 + 4 = 28，最小尺寸被定位在28和缩放的图像的新的大小之间差的一半。

（7）获取新的图像（画布+居中的图像）的像素值。

（8）归一化像素值到0和1之间的一个值（这也在TensorFlow MNIST教程中完成）。其中0是白色的，1是纯黑色。从步骤7得到的像素值是与之相反的，其中255是白色的，0黑色，所以数值必须反转。下述公式包括反转和规格化（255-X）* 1.0 / 255.0

 

结合本次实验，在刚刚训练的模型中添加如下语句：

运行之后，会发现目录中多了几个文件,这就是训练好的模型，供测试使用：

打开预测文件run_this.py文件，导入刚刚训练好的模型。也就是model2.ckpt文件。

 

模型训练1000次之后测试结果如下：

 

模型训练100次之后，再次查看结果，会发现有预测错误的情况：

所以随着训练次数的增加，预测的正确率也在不断地增加。

四、思考题

 

深度算法参数的设置对算法性能的影响？

Learning Rate（学习率）

学习率决定了权值更新的速度，设置得太大会使结果超过最优值，太小会使下降速度过慢。仅靠人为干预调整参数需要不断修改学习率。

 

Weight decay（权值衰减率）

在实际应用中，为了避免网络的过拟合，必须对价值函数（Cost function）加入一些正则项，在SGD中加入这一正则项对这个Cost function进行规范化：

公式基本思想就是减小不重要的参数对最后结果的影响，网络中有用的权重则不会受到Weight decay影响。在机器学习或者模式识别中，会出现overfitting，而当网络逐渐overfitting时网络权值逐渐变大，因此，为了避免出现overfitting,会给误差函数添加一个惩罚项，常用的惩罚项是所有权重的平方乘以一个衰减常量之和。其用来惩罚大的权值。

weightdecay（权值衰减）的使用既不是为了提高收敛精确度也不是为了提高收敛速度，其最终目的是防止过拟合。在损失函数中，weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，若weight decay很大，则复杂的模型损失函数的值也就大。

 

Momentum （激励值）

动量来源于牛顿定律，基本思想是为了找到最优加入“惯性”的影响，当误差曲面中存在平坦区域，SGD就可以更快的学习。

momentum是梯度下降法中一种常用的加速技术。对于一般的SGD，其表达式为

 

其中β即momentum系数，通俗的理解上面式子就是，如果上一次的momentum（即v）与这一次的负梯度方向是相同的，那这次下降的幅度就会加大，所以这样做能够达到加速收敛的过程。
normalization（batch normalization）。batch normalization的是指在神经网络中激活函数的前面，将按照特征进行normalization，这样做的好处有三点：

1、提高梯度在网络中的流动。Normalization能够使特征全部缩放到[0,1]，这样在反向传播时候的梯度都是在1左右，避免了梯度消失现象。

2、提升学习速率。归一化后的数据能够快速的达到收敛。

3、减少模型训练对初始化的依赖

 

Learning Rate Decay （学习衰减率）

该参数是为了提高SGD寻优能力，具体就是每次迭代的时候减少学习率的大小。

五、实验心得与体会

 

        重点是卷积神经网络，在对其中的卷积层、池化层、全连接层以及输出层进行深入了解之后，回过头再次来看CNN到底和普通神经网络有什么区别？我觉得可能在于，卷积神经网络中多了个特征抽取步骤。在卷积网络的卷积层中，一个神经元只负责处理图像信息中的特定一部分，就像识别一张人脸，我们可以使用不同的神经元来分别识别眼睛、鼻子、嘴巴或者耳朵等等，所以，在CNN的一个卷积层中，通常包含很多个特征平面，这样的每个特征平面由一些神经元组成，同一个特征平面的神经元共享权值，这里面的权值也就是卷积核。所以卷积层带来的直接好处就是减少了模型的参数。

        卷积层进行之后，通常会跟着一个池化层，这里主要有最大池化和均值池化两种，本次实验中使用的是最大池化，在池化过程中，通过特定大小的窗口简化了模型的复杂度，而且同时也保留了对应原图像部分的特征。在具体实现的过程中，我们可以设计多组卷积池化层，这样在对数据集的训练时就可以尽可能地提高正确率，在预测时最大程度上接近真实值。

       了解完这次的卷积神经网络之后，这门课的实验就结束了。总的来说，收获还蛮大的，从第一次的几种搜索算法、第二次的决策树等分类算法、第三次的强化学习算法到最后一次的深度学习算法，每一次的实验都是一次对理论知识加深理解、对新知识（weka、python等等）初步认识的过程。确实，仅仅通过课本上的内容，我们很难深入地去体会一些算法到底是怎么具体实现，通过什么来实现的，所以在做完实验之后，会明显地发现自己了解到了更多的知识，虽然过程中会遇到种种问题，或者是搞不懂算法，或者是软件出错，或者是其他各种各样的bug，但最后通过上网查各种资料、通过请教同学等等，还是用心地坚持做下来了。所以，我很感谢这门课的实验让我真正接触到人工智能的美妙之处，同时也激起了我对AI的好奇心，我会接着深入了解下去，带着兴趣。