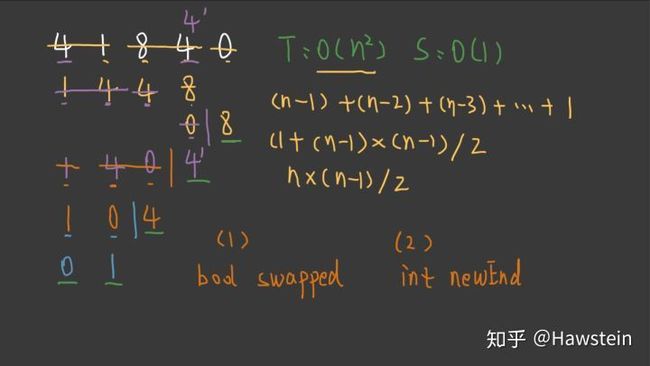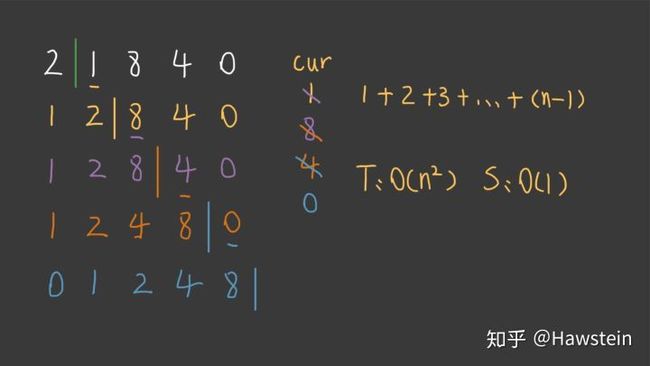十大经典排序算法视频讲解

代码仓库

代码仓库包含了完整的代码实现和测试，其中 Java 版本是官方实现，其他语言版本来自社区贡献。对于每一种排序算法，如果有多种实现方法，都会尽量提供。另外代码仓库中还提供了完备的测试用例，以此确保实现的排序算法覆盖了每一种可能的情况。

GitHub 链接：https://github.com/HawsteinStudio/algocasts-sorting-algorithms

冒泡排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/AEpoDvWQ

截图：

代码：

public class BubbleSort {

  private void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }

  // Time: O(n^2), Space: O(1)
  public void sort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    for (int end = n-1; end > 0; --end) {
      for (int i = 0; i < end; ++i) {
        if (arr[i] > arr[i+1]) {
          int tmp = arr[i];
          arr[i] = arr[i+1];
          arr[i+1] = tmp;
        }
      }
    }
  }

  // Time: O(n^2), Space: O(1)
  public void sortShort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    for (int end = n-1; end > 0; --end)
      for (int i = 0; i < end; ++i)
        if (arr[i] > arr[i+1])
          swap(arr, i, i+1);
  }

  // Time: O(n^2), Space: O(1)
  public void sortEarlyReturn(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    boolean swapped;
    for (int end = n-1; end > 0; --end) {
      swapped = false;
      for (int i = 0; i < end; ++i) {
        if (arr[i] > arr[i+1]) {
          swap(arr, i, i+1);
          swapped = true;
        }
      }
      if (!swapped) return;
    }
  }

  // Time: O(n^2), Space: O(1)
  public void sortSkip(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    int newEnd;
    for (int end = n-1; end > 0;) {
      newEnd = 0;
      for (int i = 0; i < end; ++i) {
        if (arr[i] > arr[i+1]) {
          swap(arr, i, i+1);
          newEnd = i;
        }
      }
      end = newEnd;
    }
  }

}

选择排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/Z5mzdwpd

截图：

代码：

public class SelectionSort {

  private void swap(int[] arr, int i, int j) {
    if (i == j) return;
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }

  // Time: O(n^2), Space: O(1)
  public void sort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    for (int i = 0; i < n; ++i) {
      int minIdx = i;
      for (int j = i+1; j < n; ++j)
        if (arr[j] < arr[minIdx])
          minIdx = j;
      swap(arr, i, minIdx);
    }
  }

  // Time: O(n^2), Space: O(1)
  public void sortFromEnd(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    for (int i = n-1; i > 0; --i) {
      int maxIdx = i;
      for (int j = 0; j < i; ++j)
        if (arr[j] > arr[maxIdx])
          maxIdx = j;
      swap(arr, i, maxIdx);
    }
  }

}

插入排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/dbGY9eG5

截图：

代码：

public class InsertionSort {

  // Time: O(n^2), Space: O(1)
  public void sort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    for (int i = 1; i < arr.length; ++i) {
      int cur = arr[i];
      int j = i - 1;
      while (j >= 0 && arr[j] > cur) {
        arr[j+1] = arr[j];
        --j;
      }
      arr[j+1] = cur;
    }
  }

}

希尔排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/zbmKZgWZ

截图：

代码：

public class ShellSort {

  // Time: O(n^2), Space: O(1)
  public void sort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    for (int gap = arr.length>>1; gap > 0; gap >>= 1) {
      for (int i = gap; i < arr.length; ++i) {
        int cur = arr[i];
        int j = i - gap;
        while (j >= 0 && arr[j] > cur) {
          arr[j+gap] = arr[j];
          j -= gap;
        }
        arr[j+gap] = cur;
      }
    }
  }

  // Time: O(n^2), Space: O(1)
  public void insertionSort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    for (int i = 1; i < arr.length; ++i) {
      int cur = arr[i];
      int j = i - 1;
      while (j >= 0 && arr[j] > cur) {
        arr[j + 1] = arr[j];
        j -= 1;
      }
      arr[j + 1] = cur;
    }
  }

}

快速排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/kVG9Pxmg

截图：

代码：

public class QuickSort {

  private void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }

  // [ ... elem < pivot ... | ... elem >= pivot ... | unprocessed elements ]
  //                          i                       j
  private int lomutoPartition(int[] arr, int low, int high) {
    int pivot = arr[high];
    int i = low;
    for (int j = low; j < high; ++j) {
      if (arr[j] < pivot) {
        swap(arr, i, j);
        ++i;
      }
    }
    swap(arr, i, high);
    return i;
  }

  // lomuto partition 的另一种实现，可以把最后的 swap 合并到循环中。
  private int lomutoPartition2(int[] arr, int low, int high) {
    int pivot = arr[high];
    int i = low;
    for (int j = low; j <= high; ++j) {
      if (arr[j] <= pivot) {
        swap(arr, i, j);
        ++i;
      }
    }
    return i-1;
  }

  private void lomutoSort(int[] arr, int low, int high) {
    if (low < high) {
      int k = lomutoPartition(arr, low, high);
      lomutoSort(arr, low, k-1);
      lomutoSort(arr, k+1, high);
    }
  }

  private int hoarePartitionDoWhile(int[] arr, int low, int high) {
    int pivot = arr[low + (high-low)/2];
    int i = low-1, j = high+1;
    while (true) {
      do {
        ++i;
      } while (arr[i] < pivot);
      do {
        --j;
      } while (arr[j] > pivot);
      if (i >= j) return j;
      swap(arr, i, j);
    }
  }

  // [ ... elem <= pivot ... | unprocessed elements | ... elem >= pivot ... ]
  //                         i                      j
  private int hoarePartition(int[] arr, int low, int high) {
    int pivot = arr[low + (high-low)/2];
    int i = low, j = high;
    while (true) {
      while (arr[i] < pivot) ++i;
      while (arr[j] > pivot) --j;
      if (i >= j) return j;
      swap(arr, i++, j--);
    }
  }

  private void hoareSort(int[] arr, int low, int high) {
    if (low < high) {
      int k = hoarePartition(arr, low, high);
      hoareSort(arr, low, k);
      hoareSort(arr, k+1, high);
    }
  }

  // Time: O(n*log(n)), Space: O(n)
  public void lomutoSort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    lomutoSort(arr, 0, arr.length-1);
  }

  // Time: O(n*log(n)), Space: O(n)
  public void hoareSort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    hoareSort(arr, 0, arr.length-1);
  }

}

归并排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/M0G2k7pz

截图：

代码：

public class MergeSort {

  // sorted sub-array 1: arr[low ... mid]
  // sorted sub-array 2: arr[mid+1 ... high]
  private void merge(int[] arr, int low, int mid, int high, int[] tmp) {
    int i = low, j = mid + 1, k = 0;
    while (i <= mid && j <= high) {
      if (arr[i] <= arr[j]) tmp[k++] = arr[i++];
      else tmp[k++] = arr[j++];
    }
    while (i <= mid) tmp[k++] = arr[i++];
    while (j <= high) tmp[k++] = arr[j++];
    System.arraycopy(tmp, 0, arr, low, k);
  }

  private void mergeSort(int[] arr, int low, int high, int[] tmp) {
    if (low < high) {
      int mid = low + (high - low) / 2;
      mergeSort(arr, low, mid, tmp);
      mergeSort(arr, mid + 1, high, tmp);
      merge(arr, low, mid, high, tmp);
    }
  }

  // Time: O(n*log(n)), Space: O(n)
  public void sortRecursive(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int[] tmp = new int[arr.length];
    mergeSort(arr, 0, arr.length - 1, tmp);
  }

  // Time: O(n*log(n)), Space: O(n)
  public void sortIterative(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length;
    int[] tmp = new int[n];
    for (int len = 1; len < n; len = 2*len) {
      for (int low = 0; low < n; low += 2*len) {
        int mid = Math.min(low+len-1, n-1);
        int high = Math.min(low+2*len-1, n-1);
        merge(arr, low, mid, high, tmp);
      }
    }
  }

}

堆排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/jwmBqnW8

截图：

代码：

public class HeapSort {

  private void swap(int[] arr, int i, int j) {
    int tmp = arr[i];
    arr[i] = arr[j];
    arr[j] = tmp;
  }

  // Time: O(log(n))
  private void siftDown(int[] arr, int i, int end) {
    int parent = i, child = 2 * parent + 1;
    while (child <= end) {
      if (child+1 <= end && arr[child+1] > arr[child]) ++child;
      if (arr[parent] >= arr[child]) break;
      swap(arr, parent, child);
      parent = child;
      child = 2 * parent + 1;
    }
  }

  // i 从 end/2 开始即可，因为在二叉堆中，更大的 i 是没有子节点的，没必要做 siftDown
  // Time: O(n)
  // Reference:
  // * https://www.geeksforgeeks.org/time-complexity-of-building-a-heap/
  // * https://www2.cs.sfu.ca/CourseCentral/307/petra/2009/SLN_2.pdf
  private void buildMaxHeap(int[] arr, int end) {
    for (int i = end/2; i >= 0; --i) {
      siftDown(arr, i, end);
    }
  }

  // Time: O(n*log(n)), Space: O(1)
  public void sort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    buildMaxHeap(arr, arr.length - 1);
    for (int end = arr.length - 1; end > 0; --end) {
      swap(arr, 0, end);
      siftDown(arr, 0, end - 1);
    }
  }

}

计数排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/XOp19ap2

截图：

代码：

public class CountingSort {

  // indexes 最后存储的是排序后，相同数字在结果数组的开始位置，相同数字会依次向后（右）填充。
  // Time: O(n+k), Space: O(n+k)
  public void sortLeft2Right(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int max = arr[0], min = arr[0];
    for (int num: arr) {
      if (num > max) max = num;
      if (num < min) min = num;
    }

    int k = max - min;
    int[] indexes = new int[k+1];
    for (int num: arr) ++indexes[num-min];

    int start = 0;
    for (int i = 0; i <= k; ++i) {
      int count = indexes[i];
      indexes[i] = start;
      start += count;
    }

    int[] tmp = new int[arr.length];
    for (int num: arr) {
      int idx = indexes[num-min];
      tmp[idx] = num;
      ++indexes[num-min];
    }
    System.arraycopy(tmp, 0, arr, 0, arr.length);
  }

  // indexes 最后存储的是排序后，相同数字在结果数组的结束位置，相同数字会依次向前（左）填充。
  // Time: O(n+k), Space: O(n+k)
  public void sortRight2Left(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int max = arr[0], min = arr[0];
    for (int num: arr) {
      if (num > max) max = num;
      if (num < min) min = num;
    }

    int k = max - min;
    int[] indexes = new int[k+1];
    for (int num: arr) ++indexes[num-min];

    --indexes[0];
    for (int i = 1; i <= k; ++i)
      indexes[i] = indexes[i] + indexes[i-1];

    int[] tmp = new int[arr.length];
    for (int i = arr.length-1; i >= 0; --i) {
      int idx = indexes[arr[i]-min];
      tmp[idx] = arr[i];
      --indexes[arr[i]-min];
    }
    System.arraycopy(tmp, 0, arr, 0, arr.length);
  }

}

桶排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/VBpL2omD

截图：

代码：

public class BucketSort {

  private void insertionSort(List arr) {
    if (arr == null || arr.size() == 0) return;
    for (int i = 1; i < arr.size(); ++i) {
      int cur = arr.get(i);
      int j = i - 1;
      while (j >= 0 && arr.get(j) > cur) {
        arr.set(j+1, arr.get(j));
        --j;
      }
      arr.set(j+1, cur);
    }
  }

  // 每个桶的大小，由于桶内使用插入排序，因此桶的大小使用一个较小值会比较高效。
  //
  // 一般来说，当处理的数组大小在 5-15 时，使用插入排序往往会比快排或归并更高效。
  // 因此在桶排序中，我们尽量让单个桶内的元素个数是在 5-15 个之间，这样可以用插入排序高效地完成桶内排序。
  // 参考链接：https://algs4.cs.princeton.edu/23quicksort/
  // 参考段落：
  // Cutoff to insertion sort. As with mergesort,
  // it pays to switch to insertion sort for tiny arrays.
  // The optimum value of the cutoff is system-dependent,
  // but any value between 5 and 15 is likely to work well in most situations.
  private int bucketSize;

  public BucketSort(int bucketSize) {
    this.bucketSize = bucketSize;
  }

  // Time(avg): O(n+k), Time(worst): O(n^2), Space: O(n)
  public void sort(int[] arr) {
    if (arr == null || arr.length == 0) return;
    int max = arr[0], min = arr[0];
    for (int num: arr) {
      if (num > max) max = num;
      if (num < min) min = num;
    }

    int bucketCount = arr.length / bucketSize;
    List> buckets = new ArrayList<>(bucketCount);
    for (int i = 0; i < bucketCount; ++i)
      buckets.add(new ArrayList<>());

    for (int num: arr) {
      int idx = (int)((num - min) / (max - min + 1.0) * bucketCount);
      buckets.get(idx).add(num);
    }

    int idx = 0;
    for (List bucket: buckets) {
      insertionSort(bucket);
      for (int num: bucket)
        arr[idx++] = num;
    }
  }

}

基数排序

视频链接：https://algocasts.io/series/sorting-algorithms/episodes/q2m595mz

截图：

代码：

public class RadixSort {

  /**
   * @param arr  待排数组
   * @param bits 每次处理的二进制位数（可选值：1, 2, 4, 8, 16）
   * @param mask 每次移动 bits 个二进制位后，使用 mask 取出最低的 bits 位。
   */
  // b 表示每次处理的二进制位数
  // Time: O(32/b * n), Space: O(n + 2^b)
  private void sort(int[] arr, int bits, int mask) {
    if (arr == null || arr.length == 0) return;
    int n = arr.length, cnt = 32/bits;
    int[] tmp = new int[n];
    int[] indexes = new int[1<> (bits*d)) & mask;
        ++indexes[idx];
      }

      --indexes[0];
      for (int i = 1; i < indexes.length; ++i)
        indexes[i] = indexes[i] + indexes[i-1];

      for (int i = n-1; i >= 0; --i) {
        int idx = (arr[i] >> (bits*d)) & mask;
        tmp[indexes[idx]] = arr[i];
        --indexes[idx];
      }

      Arrays.fill(indexes, 0);
      int[] t = arr;
      arr = tmp;
      tmp = t;
    }
    // handle the negative number
    // get the length of positive part
    int len = 0;
    for (; len < n; ++len)
      if (arr[len] < 0) break;

    System.arraycopy(arr, len, tmp, 0, n-len); // copy negative part to tmp
    System.arraycopy(arr, 0, tmp, n-len, len); // copy positive part to tmp
    System.arraycopy(tmp, 0, arr, 0, n); // copy back to arr
  }

  // 基数为 256，每次取 8 个二进制位作为一个部分进行处理，32 位整数需要处理 4 次。
  // 每次取出的 8 个二进制位会作为计数排序的键值，去排序原始数据。
  // 每次处理 8 个二进制位，是时间/空间上比较折衷的方法。
  // 如果一次处理 16 个二进制位，速度会稍微快一些。但需要额外的空间是 2^16 = 65536，远大于每次处理 8 个二进制位所需空间。
  // 如果一次只处理 4 个二进制位，速度则会慢很多。
  public void sort4pass(int[] arr) {
    sort(arr, 8, 0xff);
  }

  // 基数为 16，每次取 4 个二进制位作为一个部分进行处理。32 位整数需要处理 8 次。
  // 时间上比起 sort4pass 要差很多。
  public void sort8pass(int[] arr) {
    sort(arr, 4, 0x0f);
  }

  // 基数为 65536，每次取 16 个二进制位作为一个部分进行处理。32 位整数需要处理 2 次。
  // 时间上比 sort4pass 要稍微好一些，但额外要使用多得多的空间。
  public void sort2pass(int[] arr) {
    sort(arr, 16, 0xffff);
  }

  // 基数为 2，每次取 1 个二进制位作为一个部分进行处理。32 位整数需要处理 32 次。
  // 时间上比快排要差很多。
  public void sort32pass(int[] arr) {
    sort(arr, 1, 1);
  }

  // 基数为 4，每次取 2 个二进制位作为一个部分进行处理。32 位整数需要处理 16 次。
  // 我是打酱油的。
  public void sort16pass(int[] arr) {
    sort(arr, 2, 3);
  }

}