卡尔曼滤波、扩展卡尔曼滤波、无迹卡尔曼滤波以及粒子滤波原理

所有滤波问题其实都是求感兴趣的状态的后验概率分布，只是由于针对特定条件的不同，可通过求解递推贝叶斯公式获得后验概率的解析解（KF、EKF、UKF），也可通过大数统计平均求期望的方法来获得后验概率（PF）。

1 KF、EKF、UKF

1.1 定义

KF、EKF、UKF 都是一个隐马尔科夫模型与贝叶斯定理的联合实现。是通过观测信息及状态转移及观测模型对状态进行光滑、滤波及预测的方法。而KF、EKF及UKF的滤波问题都可以通过贝叶斯估计状态信息的后验概率分布来求解。Kalman在线性高斯的假设下，可以直接获得后验概率的解析解；EKF是非线性高斯模型，通过泰勒分解将非线性问题转化为线性问题，然后套用KF的方法求解，缺陷是线性化引入了线性误差且雅克比、海塞矩阵计算量大；而UKF也是非线性高斯模型，通过用有限的参数来近似随机量的统计特性，用统计的方法计算递推贝叶斯中各个积分项，从而获得了后验概率的均值和方差。

1.2 原理

KF、EKF、UKF滤波问题是一个隐马尔科夫模型与贝叶斯定理的联合实现。一般的状态模型可分为状态转移方程和观测方程，而状态一般都是无法直接观测到的，所以时隐马尔科夫模型。然后，它将上一时刻获得的状态信息的后验分布作为新的先验分布，利用贝叶斯定理，建立一个贝叶斯递推过程，从而得到了贝叶斯递推公式，像常用的卡尔曼滤波、扩展卡尔曼滤波、不敏卡尔曼滤波以及粒子滤波都是通过不同模型假设来近似最优贝叶斯滤波得到的。这也是滤波问题的基本思路。所有贝叶斯估计问题的目的都是求解感兴趣参数的后验概率密度。
并且后验概率的求解是通过递推计算目标状态后验概率密度的方法获得的。在贝叶斯框架下，通过状态参数的先验概率密度和观测似然函数来求解估计问题；在目标跟踪背景下（隐马尔科夫模型），目标动态方差决定状态转移概率，观测方程决定释然函数。一般化的整个计算过程可以分为3步：
01. 一步状态预测：通过状态转移概率及上一时刻的后验概率算出一步预测概率分布。从而得到状态预测的均值和方差
02. 归一化系数计算：通过对似然函数与一步状态预测概率的乘积中的状态进行积分，可以得到观测转移的概率分布，从而得到目标观测的均值和方差，并可算出卡尔曼增益（用来权衡预测与观测对状态滤波的贡献）
03. 然后利用递推贝叶斯公式算得状态的后验概率，从而得到目标状态的均值和方差【高斯乘积定理】
其中KF可以直接得到解析解，EKF通过泰勒分解线性化后可得到解析解，而UKF通过在定义域按一定规则采样来近似获得后验状态的均值和方差，但这些样本点的要求是样本均值和方差收敛于真正的均值和方差，不过已经有许多学者提出了相关的采样方法。

1.2.1 Kalmanlfilter:

动态方程和观测方程式线性高斯的，且k-1时刻的后验密度也是高斯的，【近似高斯分布使得计算很方便，仅用均值和方差就可以完全界定高斯分布，并且这一假设在实际应用中效果也是非常好，】
主要就是实现贝叶斯递推公式的求解，需要有概率、矩阵、积分运算的基本知识，在结合高斯乘积定理。

1.2.2 扩展kalmanfilter：

是一个简单的非线性近似滤波算法，指运动方差或观测方程不是线性的情况。为了简化计算，EKF通过一阶泰勒分解线性化运动/观测方程。KF与EKF具有相同的算法结构，都是以高斯形式描述后验概率密度的，都是通过计算贝叶斯递推公式得到的。最大的不同之处在于，计算方差时，EKF的状态转移矩阵（上一时刻的状态信息k-1|k-1）和观测矩阵（一步预测k|k-1）都是状态信息的雅克比矩阵。主要问题如下：
1. 运动及观察模型用泰勒级数的一阶或二阶展开近似成线性模型，忽略了高阶项，不可避免的引入线性误差，甚至导致滤波器发散。有如下误差补偿方法：
泰勒近似使得状态预测必然存在误差：
A) 补偿状态预测中的误差，附加“人为过程噪声”，即通过增大过程噪声协方差来实现这一点。
B) 扩大状态预测协方差矩阵，用标量加权因子φ>1乘状态预测协方差矩阵
C) 利用对角矩阵φ=diag(sqrt(φi)), φi>1来乘以状态预测协方差矩阵
其实无论增大过程噪声协方差还是状态预测协方差矩阵，都是为了增大kalman增益，即状态预测是不准的，我要减小一步状态预测在状态更新中的权重。
2. 雅克比矩阵（一阶）及海塞矩阵（二阶）计算困难。二阶EKF的性能要好于一阶的，而二阶以上的性能相比于二阶并没有太大的提高，所以超过二阶以上的EKF一般不采用。但二阶EKF的性能虽好，但计算量大，一般情况下不用

1.2.3 无迹kalman滤波

前面的KF和EKF都是都将问题转化为线性高斯模型，所以可以直接解出贝叶斯递推公式中的解析形式，方便运算。但对于非线性问题，EKF除了计算量大，还有线性误差的影响，所以这里引入UKF。对于求解非线性模型的贝叶斯递推公式的主要困难在于如何解析的求解一步预测状态分布的概率、（观测方程得到的）似然函数分布密度以及后验条件概率的分布，EKF利用泰勒分解将模型线性化，在利用高斯假设解决了概率计算困难的问题。但是线性误差的引入降低了模型精度。那么我们换个思路，对于非线性模型，直接用解析的方式来求解贝叶斯递推公式比较困难主要很难解析的得到各个概率分布的均值和方差，但不敏变换（一种计算非线性随机变量各阶矩的近似方法）却可以较好的解决这个问题，通过一定规律的采样和权重，可以近似获得均值和方差。而且由于不敏变换对统计矩的近似精度较高，UKF的效果可以达到二阶EKF的效果。
详细的推导过程如下图所示，由于EKF及UKF都是KF的扩展版本，所以推导过程极为相似。【详细的推导可以参考 [机器学习方法原理及编程实现–07.隐马尔科夫及其在卡尔曼滤波中的应用][1].】
[1]https://blog.csdn.net/drilistbox/article/details/79886714

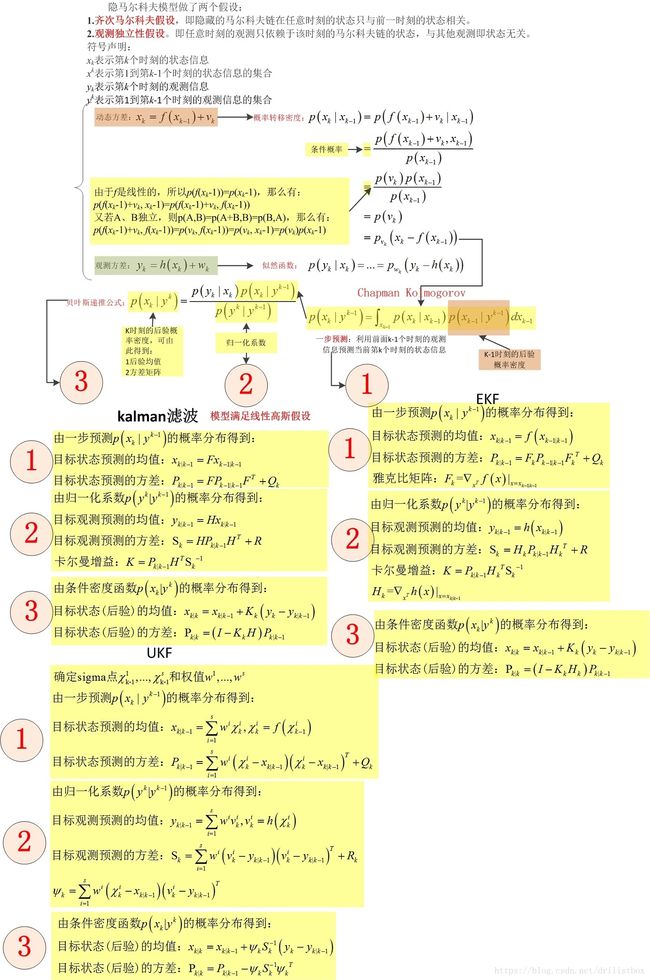
KF、EKF及UKF均较为简单，且网上有大量的开源算例，这里不再累述。

2 粒子滤波

2.1 定义

粒子滤波也是一种非线性算法，是基于门特卡罗仿真的最后回归贝叶斯滤波算法，通过对后验概率密度进行数值近似求解，感觉是完全从大数定理统计的角度来解决问题。它将关心的状态矢量表示为一组带有权值的随机样本，并且基于这些样本和权值可以计算出状态估值。该方法没有模型或高斯噪声的限制。

2.2 原理

滤波问题中的困难主要在于后验概率的计算，粒子滤波的出发点是：只要从后验概率中采样很多粒子，用它们的状态求平均就得到了滤波结果。
1. 引入蒙特卡洛随机采样来计算后验概率，从统计上获得状态的均值（后验概率分布的期望）
2. 但由于采样时无法直接知道后验概率的分布，所以引入重要性采样这个方法，通过公式变换将问题转化为从已知分布中进行采样去计算粒子权值；
3. 然后又通过马尔科夫性将权重计算转换成序贯权重计算（SIS）
4. 通过残差重采样避免了权重消失现象。（SIS+重采样=标准的粒子滤波）
5. 重要性概率密度函数=状态转移概率，简化粒子权重计算（SIR）

2.2.1 kf/ekf/ukf与pf有什么区别和联系

相同点：都是求后验概率
不同点：条件的差别导致了求解方法的差别，由于kf/ekf/ukf都是高斯噪声，所以不论模型线性与否都能得到近似近似解析解，而pf没有模型限定，因此是Kf是通过求解递推贝叶斯公式来得到后验概率分布的，而pf直接通过带权重的随机样本统计后验概率的均值。

2.2.2 门特卡罗

2.2.3 重要性采样

2.2.4 序贯重要性采样（SIS）

2.2.4.1 重采样

2.2.4.1.1 标准的粒子滤波算法（sis+重采样）

2.2.4.2 SIR滤波器 （重要性概率密度函数=状态转移概率，简化粒子权重计算）

2.2.4.2.1 SIR滤波器流程

2.2.5 算例实现

2.2.5.1 算例实现1：非线性运动模型的状态估计

代码实现：

clear all
close all
clc
x = 0.1; % initial actual state
x_N = 1; % 系统过程噪声的协方差(由于是一维的，这里就是方差)
x_R = 1; % 测量的协方差
T = 75;  % 总的时刻数
N = 100; % 粒子数，越大效果越好，计算量也越大

V = 2; %初始分布的方差
x_P = []; % 粒子
% 粒子集初始化，按初始先验概率(这里设为高斯分布)生成初始粒子集合
for i = 1:N
    x_P(i) = x + sqrt(V) * randn;
end

z_out = [x^2 / 20 + sqrt(x_R) * randn];  %实际测量值
x_out = [x]; 
x_est = [x]; 
x_est_out = [x_est]; 

for t = 1:T
    x = 0.5*x + 25*x/(1 + x^2) + 8*cos(1.2*(t-1)) +  sqrt(x_N)*randn;
    z = x^2/20 + sqrt(x_R)*randn;
    for i = 1:N
        %根据状态转移函数计算粒子的一步预测
        x_P_update(i) = 0.5*x_P(i) + 25*x_P(i)/(1 + x_P(i)^2) + 8*cos(1.2*(t-1)) + sqrt(x_N)*randn;
        %根据观测方程计算采样粒子的观测值
        z_update(i) = x_P_update(i)^2/20;
        %利用似然函数更新权重
        P_w(i) = (1/sqrt(2*pi*x_R)) * exp(-(z - z_update(i))^2/(2*x_R));
        %由于重采样后的权重为均匀分布，所以在计算未归一化的权重时可以不再乘以上一时刻的权重
    end
    % 归一化.
    P_w = P_w./sum(P_w);
    %残差重采样
    for i = 1 : N
        x_P(i) = x_P_update(find(rand <= cumsum(P_w),1));   % 粒子权重大的将多得到后代
    end                                                     % find( ,1) 返回第一个符合前面条件的数的下标

    %状态估计，重采样以后，每个粒子的权重都变成了1/N
    x_est = mean(x_P);
%     x_est = sum(P_w.*x_P_update);

    x_out = [x_out x];
    z_out = [z_out z];
    x_est_out = [x_est_out x_est];
end

t = 0:T;
figure(1);
clf
plot(t, x_out, '.-b', t, x_est_out, '-.r','linewidth',3);
set(gca,'FontSize',12); set(gcf,'Color','White');
xlabel('time step'); ylabel('flight position');
legend('True flight position', 'Particle filter estimate');

2.2.5.2 算例实现2：视频中红色像素点跟踪

代码实现：https://pan.baidu.com/s/1qZLJ7Gg

3 但这些方法都有优缺点：

KF优点：计算简单
KF缺点：高斯线性模型约束
EKF优点：可以近似非线性问题
EKF缺点：高斯噪声约束，线性化引入了误差会可能导致滤波发散，雅克比矩阵（一阶）及海塞矩阵（二阶）计算困难
UKF优点：模型无损失，计算精度高
UKF缺点：高斯噪声约束
Kf是最优贝叶斯滤波的解析解，ekf和ekf是最优贝叶斯滤波的解析近似解。虽然ukf和ekf的计算效率很高，但是他们的计算精度受到有效性的限制，若有足够的计算资源，通过对后验概率密度进行数值近似可以提高计算进度。

PF优点：模型噪声无限制，原理简单，
PF缺点：计算量大，为了减缓权重缩减而引入重抽样，限制了算法的平行计算；抽样枯竭【具有较大权值的粒子将多出选中，使得现存的粒子不在能代表现有的概率密度，当过程噪声较小时，所有粒子讲可能转变为一个单一的点】，正则粒子滤波好像可以减轻这种现象，但我还没看。
推荐看看无味卡尔曼滤波（UKF）,他是有选择的产生粒子，粒子的权重均值和方差收敛于真正的均值和方差，
而PF是随机产生(按指定分布产生)。