一、神经网络 -- 从感知机讲起

本篇博客主要内容参考图书《神经网络与深度学习》，李航博士的《统计学习方法》National Taiwan University (NTU)李宏毅老师的《Machine Learning》的课程，在下文中如果不正确的地方请积极指出。
如果喜欢请点赞，欢迎评论留言 ！ o(￣▽￣)ブ

1. 感知机、sigmoid神经元与逻辑回归之间的关系

  感知机是一种十分简单易实现的机器学习方法，但是它也是很多知名方法的起源，比如说 SVM 以及之后要介绍的神经网络。下面将从感知机、sigmoid神经元与逻辑回归三个方面介绍，因为本系列文章主要针对神经网络与深度学习，所以对于感知机和逻辑回归部分的介绍会比较简单，感兴趣的同学可以参考李航博士的《统计学习方法》。

1.1 感知机

  感知机是由科学家Frank Rosenblatt发明于1950至1960年代，它受到了Warren McCulloch 和Walter Pitts的更早工作的启发。其具体结构如图1所示

图1. 感知机结构图

其中的 x x 是感知机的输入，一个感知机还可以有更多的输入，但这些输入都必须是二进制的输入； w1,w2 w 1 , w 2 是表示各个输入对于输出的重要程度，称为权重。
  感知机的输出是1还是0主要通过下式进行判断

f(n)={0,1,if  ∑jwjxj≤ thresholdif  ∑jwjxj> threshold(1) (1) f ( n ) = { 0 , if    ∑ j w j x j ≤  threshold 1 , if    ∑ j w j x j >  threshold

  我们可以将感知机的书写方法进行简化，首先将上式中的求和运算用向量相乘的形式进行表示，其次用偏移值 b b (bias)来代替阈值threshold，于是感知机的表达形式可以写成如下的形式

f(n)={0,1,if  wx+b≤ 0if  wx+b> 0(2) (2) f ( n ) = { 0 , if    w x + b ≤  0 1 , if    w x + b >  0

  从上式可以明显的看出 偏移值 b b 是一种对神经元被激活程度的度量。当然一个感知机也可以通过构复杂的网络构成更精细的决策方式。

1.2 sigmoid神经元

  sigmoid神经元与感知机相比做了一些修改，使得它在轻微改变其权值和偏移时只会引起小幅度的输出变化，进而防止轻微改变网络中任何一个感知机的权值或偏移有时甚至会导致感知机的输出完全翻转，并且可能以某种非常复杂的方式彻底改变网络中其余部分的现象出现。
  sigmoid神经元的具体形式如图2所示

图2. 神经元结构图

它的数学表达形式为

f(w, x)=11+e−∑jwjxj−b(3) (3) f ( w ,   x ) = 1 1 + e − ∑ j w j x j − b

  将sigmoid函数的图像及其阶跃函数的图像绘制出来如图3所示

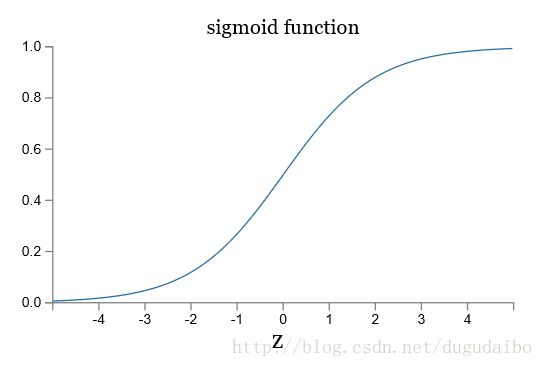
图3. sigmoid函数图像及其阶跃函数图像

  将sigmoid神经元中的sigmoid函数换为阶梯函数（阶跃函数）即可以得到之前介绍的感知机，因此感知机与sigmoid神经元是十分相似的。不同的地方在于sigmoid函数使我们就得到了一个平滑的感知机，也正是因为这个平滑的感知机使得选择权值(w)和偏移(b)的轻微改变 量并使输出按照预期发生小幅度变化成为易事。

1.3 逻辑回归

  二项逻辑回归的模型是如下的条件概率模型

P(Y=1|x)=exp(w⋅x+b)1+exp(w⋅x+b)(4) (4) P ( Y = 1 | x ) = e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x + b )

P(Y=0|x) = \frac{1}{1+exp(w\cdot x+b)}\tag{5}\label{5} P(Y=0|x) = \frac{1}{1+exp(w\cdot x+b)}\tag{5}\label{5}

我们可以看到其中的 P(Y=0|x) P ( Y = 0 | x ) 实际上是sigmoid 函数的形式化表述。

  之后考察逻辑回归模型的特点。一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值（请注意是几率不是概率）。 如果事件发生的概率是 p p ，那么该事件的几率是 1−p 1 − p ，该事件的对数几率（log odds）或logit函数是：

logit(p)=log(p1−p) l o g i t ( p ) = l o g ( p 1 − p )

对于逻辑回归而言：

log(p(Y=1|x)1−P(Y=1|x))=w⋅x l o g ( p ( Y = 1 | x ) 1 − P ( Y = 1 | x ) ) = w ⋅ x

  在逻辑斯蒂回归模型中，输出 Y=1 Y = 1 的对数几率是输入 x x 的线性函数。或者说，输出Y=1的对数几率是由属于x的线性函数表示的模型，即逻辑斯蒂回归模型；从另外一个角度观察，公式（4）通过逻辑回归模型，将线性函数 w⋅x w ⋅ x 转换为概率。

  所以感知机与逻辑回归之间的关系就是，感知机只通过决策函数 w⋅x w ⋅ x 的符号来判断属于哪一类；而逻辑斯蒂回归需要再进一步，它要找到分类概率P(Y=1)与输入向量x的直接关系，再通过比较概率值来判断类别。

2. 迈向深度学习

  我们采用图4的这种方式试图理解神经网络进行分类的。

图4. 理解神经网络的工作模式

它将一个人脸检测问题转化为对于图像每一个小部分的检测，如在左上角是否一个眼睛等。之后为了检测这个眼镜是否存在，又将检测眼睛的工作进一步分解为如图5的几个部分

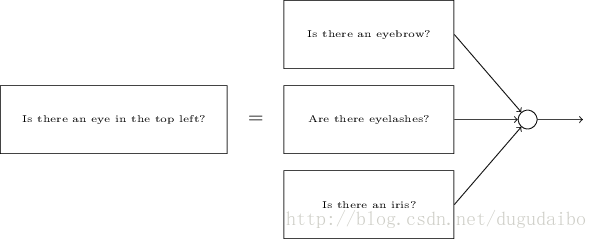
图5. 将其中的一个检测部分继续分解

  最终的结果是，我们设计出了一个网络，它将一个非常复杂的问题——这张图像是否有一张人脸——分解成在单像素层面上就可回答的非常简单的问题。在前面的网络层，它回答关于输入图像非常简单明确的问题，在后面的网络层，它建立了一个更加复杂和抽象的层级结构。包含这种多层结构（两层或更多隐含层）的网络叫做深度神经网络（deep neural network）。