Python时频变换(傅里叶变换)

参考博客：

https://blog.csdn.net/on2way/article/details/46981825
https://www.cnblogs.com/ranjiewen/p/6241913.html
参考书籍：
《数字图像处理第三版》（冈萨雷斯）
《信号与系统第二版》（奥本海姆）

本博客不会讲述过多的公式与证明（我不会说在博客输入公式好麻烦）。

傅里叶提出，任何周期函数可以表示为不同频率的正弦和/或余弦和的形式。无论函数多复杂，只要它是周期的，并且满足某些适度的数学条件，都可以用这样的和表示。甚至非周期函数（但该曲线下的面积是有限的）也可以用正弦和/或余弦和乘以加权函数的积分来表示。用傅里叶级数或者变换表示的函数特征完全可以通过傅里叶反变换来重建，而不会丢失任何信息。这是这种表示方法的最重要特征之一：不丢失任何信息。

而数字图像，尤其是计算机所能识别的图像可以说都是离散信号，并且以二维居多。

连续信号傅里叶变换： (1)

连续傅里叶反变换： (2)
公式(1)与公式(2)合称为傅里叶变换对。

而二维连续傅里叶变换对：
(3)
和： （4）

而二维离散傅里叶变换（DFT）：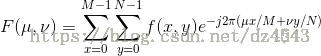
二维离散傅里叶反变换(IDFT)：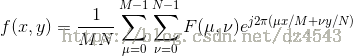

而通常二维DFt一般式复函数，故可用极坐标系表示为：

其中，幅值(也称频谱）：

相角：

功率谱：

• 傅里叶变换

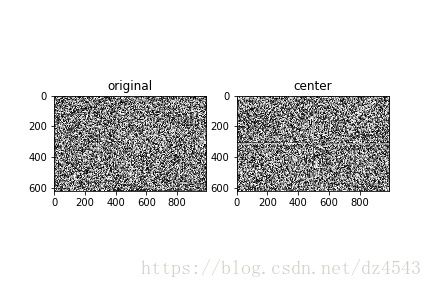
那么对一张图做傅里叶变换后会怎样的？变换前：

变换后：

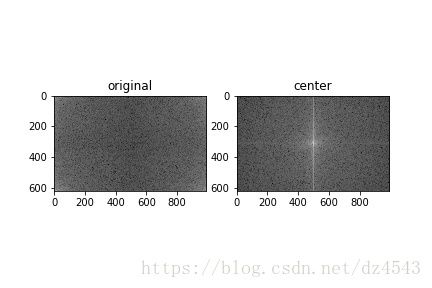
代码如下：`
import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread(‘D:/codes/shan.jpg’,0) #直接读为灰度图像
f = np.fft.fft2(img)#二维傅里叶变换
fshift = np.fft.fftshift(f)#将频谱对称轴从左上角移至中心

plt.subplot(121),plt.imshow(f,‘gray’),plt.title(‘original’)
plt.subplot(122),plt.imshow(fshift,‘gray’),plt.title(‘center’)

plt.savefig(“examples.jpg”)
`
为什么会用到fftshift（），将频谱从左上角移至中心？傅里叶变换将低频信号放在了边缘，高频信号放在了中间，然而一副图像，很明显的低频信号多而明显，所以讲低频信号移至中心。我们将傅里叶变换后的数据称为频域，变换前称为空域。

那么相位图呢？

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('flower.jpg',0) #直接读为灰度图像
f = np.fft.fft2(img)
fshift = np.fft.fftshift(f)
#取绝对值：将复数变化成实数
#取对数的目的为了将数据变化到较小的范围（比如0-255）
ph_f = np.angle(f)#前面傅里叶变换的结果是复数，可以直接用angle函数求角度
ph_fshift = np.angle(fshift)

plt.subplot(121),plt.imshow(ph_f,'gray'),plt.title('original')
plt.subplot(122),plt.imshow(ph_fshift,'gray'),plt.title('center')

• 傅里叶逆变换
  代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('D:/codes/shan.jpg',0) #直接读为灰度图像
f = np.fft.fft2(img)#二维傅里叶变换
fshift = np.fft.fftshift(f)#将频谱对称轴从左上角移至中心

#取绝对值：将复数变化成实数
#取对数的目的为了将数据变化到较小的范围（比如0-255）
s1 = np.log(np.abs(f))
s2 = np.log(np.abs(fshift))

#ph_f=np.angle(f)
#ph_fshift = np.angle(fshift)


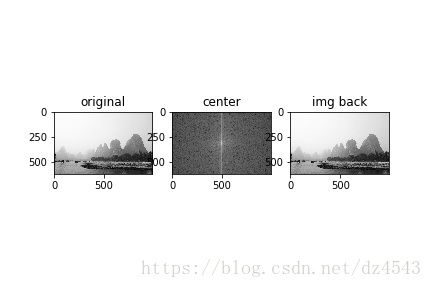
plt.subplot(131),plt.imshow(img,'gray'),plt.title('original')
plt.subplot(132),plt.imshow(s2,'gray'),plt.title('center')


# 逆变换
f1shift = np.fft.ifftshift(fshift)
img_back = np.fft.ifft2(f1shift)
#出来的是复数，无法显示
img_back = np.abs(img_back)
plt.subplot(133),plt.imshow(img_back,'gray'),plt.title('img back')
plt.savefig("examples.jpg")

可以看到恢复的一样