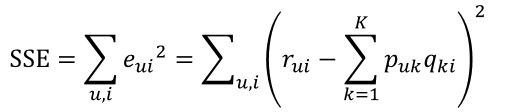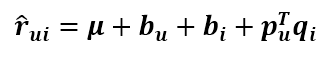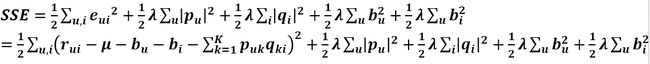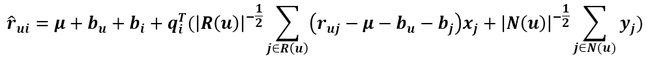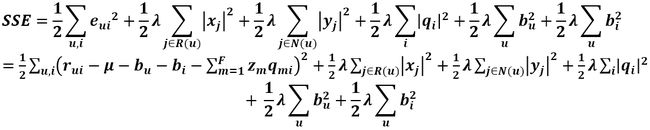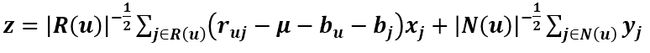【推荐系统】协同过滤（CF）算法详解，item-base，user-based，SVD，SVD++

协同过滤算法

协同过滤(Collaborative Filtering, 简称 CF)是利用集体智慧的一个典型方法。要理解什么是协同过滤 ，首先想一个简单的问题，如果你现在想看个电影，但你不知道具体看哪部，你会怎么做？大部分的人会问问周围的朋友，看看最近有什么好看的电影推荐，而我们一般更倾向于从口味比较类似的朋友那里得到推荐。这就是协同过滤的核心思想。

CF算法是推荐算法的一个大分支，基本思想是推荐相似的物品，或者推荐相似用户（隐式或者显式）评分过的物品。CF方法主要可以分为两类：基于邻域和基于隐语义。

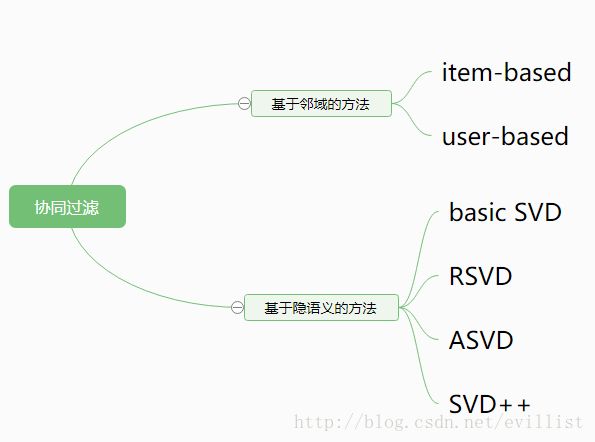
1. 基于邻域的方法

1.1 收集用户行为

要从用户的行为和偏好中发现规律，并基于此给予推荐，如何收集用户的偏好信息成为系统推荐效果最基础的决定因素。用户有很多方式向系统提供自己的偏好信息，而且不同的应用也可能大不相同。不是本文的重点，不详细介绍，请看[5].

1.2 找到相似的用户或物品

在上一步中，通过收集用户的行为，分别得到描述用户和物品的特征向量，进一步计算相似度和找到物品/用户的相似邻居。

下面看两种相似度计算方法：

• 假设 x，y 是 n 维空间的两个点，欧式距离：

当用欧几里德距离表示相似度，一般采用以下公式进行转换：距离越小，相似度越大

• 皮尔逊相关系数一般用于计算两个定距变量间联系的紧密程度，它的取值在 [-1，+1] 之间

另外，还有Cosine 相似度和Tanimoto 系数被广泛应用于计算文档数据的相似度，详见[5]。

介绍完相似度的计算方法，下面我们看看如何根据相似度找到用户/物品的邻居，常用的挑选邻居的原则可以分为两类：图 1 给出了二维平面空间上点集的示意图

• 固定数量的邻居：K-neighborhoods 或者 Fix-size neighborhoods

不论邻居的“远近”，只取最近的 K 个，作为其邻居。如图 1 中的 A，假设要计算点 1 的 5- 邻居，那么根据点之间的距离，我们取最近的 5 个点，分别是点 2，点 3，点 4，点 7 和点 5。但很明显我们可以看出，这种方法对于孤立点的计算效果不好，因为要取固定个数的邻居，当它附近没有足够多比较相似的点，就被迫取一些不太相似的点作为邻居，这样就影响了邻居相似的程度，比如图 1 中，点 1 和点 5 其实并不是很相似。

• 基于相似度阈值的邻居：Threshold-based neighborhoods
  与计算固定数量的邻居的原则不同，基于相似度门槛的邻居计算是对邻居的远近进行最大值的限制，落在以当前点为中心，距离为 K 的区域中的所有点都作为当前点的邻居，这种方法计算得到的邻居个数不确定，但相似度不会出现较大的误差。如图 1 中的 B，从点 1 出发，计算相似度在 K 内的邻居，得到点 2，点 3，点 4 和点 7，这种方法计算出的邻居的相似度程度比前一种优，尤其是对孤立点的处理。
• 计算推荐。
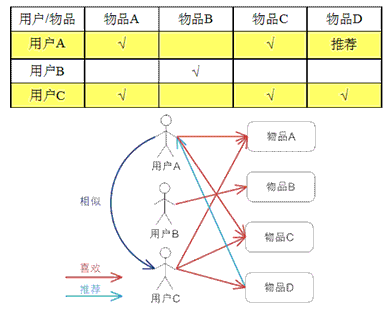
  基于用户的 CF 的基本思想相当简单，基于用户对物品的偏好找到相邻邻居用户，然后将邻居用户喜欢的推荐给当前用户。计算上，就是将一个用户对所有物品的偏好作为一个向量来计算用户之间的相似度，找到 K 邻居后，根据邻居的相似度权重以及他们对物品的偏好，预测当前用户没有偏好的未涉及物品，计算得到一个排序的物品列表作为推荐。图 2 给出了一个例子，对于用户 A，根据用户的历史偏好，这里只计算得到一个邻居 - 用户 C，然后将用户 C 喜欢的物品 D 推荐给用户 A。

基于物品的 CF 的原理和基于用户的 CF 类似，只是在计算邻居时采用物品本身，而不是从用户的角度，即基于用户对物品的偏好找到相似的物品，然后根据用户的历史偏好，推荐相似的物品给他。从计算的角度看，就是将所有用户对某个物品的偏好作为一个向量来计算物品之间的相似度，得到物品的相似物品后，根据用户历史的偏好预测当前用户还没有表示偏好的物品，计算得到一个排序的物品列表作为推荐。图 3 给出了一个例子，对于物品 A，根据所有用户的历史偏好，喜欢物品 A 的用户都喜欢物品 C，得出物品 A 和物品 C 比较相似，而用户 C 喜欢物品 A，那么可以推断出用户 C 可能也喜欢物品 C。

1.4 适应场景和优缺点

• 计算复杂度

对于一个在线网站，用户的数量往往大大超过物品的数量，同时物品的数据相对稳定，因此计算物品的相似度不但计算量较小，同时也不必频繁更新，此时item-based更优。但我们往往忽略了这种情况只适应于提供商品的电子商务网站，对于新闻，博客或者微内容的推荐系统，情况往往是相反的，物品的数量是海量的，同时也是更新频繁的，所以单从复杂度的角度，这两个算法在不同的系统中各有优势，推荐引擎的设计者需要根据自己应用的特点选择更加合适的算法。

• 适用场景

在非社交网络的网站中，内容内在的联系是很重要的推荐原则，它比基于相似用户的推荐原则更加有效。比如在购书网站上，当你看一本书的时候，推荐引擎会给你推荐相关的书籍，这个推荐的重要性远远超过了网站首页对该用户的综合推荐。可以看到，在这种情况下，Item CF 的推荐成为了引导用户浏览的重要手段。同时 Item CF 便于为推荐做出解释，在一个非社交网络的网站中，给某个用户推荐一本书，同时给出的解释是某某和你有相似兴趣的人也看了这本书，这很难让用户信服，因为用户可能根本不认识那个人；但如果解释说是因为这本书和你以前看的某本书相似，用户可能就觉得合理而采纳了此推荐。

相反的，在现今很流行的社交网络站点中，User-based 是一个更不错的选择，User-based加上社会网络信息，可以增加用户对推荐解释的信服程度。
- 推荐多样性和精度

研究推荐引擎的学者们在相同的数据集合上分别用 User CF 和 Item CF 计算推荐结果，发现推荐列表中，只有 50% 是一样的，还有 50% 完全不同。但是这两个算法确有相似的精度，所以可以说，这两个算法是很互补的。

关于推荐的多样性，有两种度量方法：

第一种度量方法是从单个用户的角度度量，就是说给定一个用户，查看系统给出的推荐列表是否多样，也就是要比较推荐列表中的物品之间两两的相似度，不难想到，对这种度量方法，Item CF 的多样性显然不如 User CF 的好，因为 Item CF 的推荐就是和以前看的东西最相似的。

第二种度量方法是考虑系统的多样性，也被称为覆盖率 (Coverage)，它是指一个推荐系统是否能够提供给所有用户丰富的选择。在这种指标下，Item CF 的多样性要远远好于 User CF, 因为 User CF 总是倾向于推荐热门的，从另一个侧面看，也就是说，Item CF 的推荐有很好的新颖性，很擅长推荐冷门的物品。所以，尽管大多数情况，Item CF 的精度略小于 User CF， 但如果考虑多样性，Item CF 却比 User CF 好很多。

前面我们大部分都是从推荐引擎的角度考虑哪个算法更优，但其实我们更多的应该考虑作为推荐引擎的最终使用者 – 应用用户对推荐算法的适应度。

• 用户对推荐算法的适应度

对于 User CF，推荐的原则是假设用户会喜欢那些和他有相同喜好的用户喜欢的东西，但如果一个用户没有相同喜好的朋友，那 User CF 的算法的效果就会很差，所以一个用户对的 CF 算法的适应度是和他有多少共同喜好用户成正比的。

Item CF 算法也有一个基本假设，就是用户会喜欢和他以前喜欢的东西相似的东西，那么我们可以计算一个用户喜欢的物品的自相似度。一个用户喜欢物品的自相似度大，就说明他喜欢的东西都是比较相似的，也就是说他比较符合 Item CF 方法的基本假设，那么他对 Item CF 的适应度自然比较好；反之，如果自相似度小，就说明这个用户的喜好习惯并不满足 Item CF 方法的基本假设，那么对于这种用户，用 Item CF 方法做出好的推荐的可能性非常低。

基于邻域方法的缺点是：由于实际用户评分的数据是十分稀疏，用户之间可能根本没有相同的评论；而且用启发式的方法很难考虑全面用户和物品之间的所有关系
　　

2. 基于隐语义的方法

基于隐语义的方法则不依赖于共同评分。其基本思想是将用户和物品分别映射到某种真实含义未知的特征向量。
两种向量可以包含一定的含义，比如，将user的兴趣表示为4维向量，分别代表：
1.对颜色的偏好
2.对重量的要求
3.设计风格的偏好
4.价格偏好
相应地，item对应的特点也表示为4维向量:
1.颜色
2.重量
3.设计风格
4.价格
然后通过两个特征向量的内积来判断用户对一个物品的喜好程度。在具体的模型中，向量每个维度的意义并不能人为给定，模型会自己通过最小化损失来学习这两个向量。虽然这个方法不要求共同评分，但推荐系统还是面临很大的数据稀疏问题。

2.1 Basic SVD和RSVD

下面开始介绍SVD算法，假设存在以下user和item的数据矩阵：

这是一个极其稀疏的矩阵，这里把这个评分矩阵记为R，其中的元素表示user对item的打分，“？”表示未知的，也就是要你去预测的，现在问题来了：如何去预测未知的评分值呢？上一篇文章用SVD证明了对任意一个矩阵A，都有它的满秩分解：

么刚才的评分矩阵R也存在这样一个分解，所以可以用两个矩阵P和Q的乘积来表示评分矩阵R：

上图中的U表示用户数，I表示商品数。然后就是利用R中的已知评分训练P和Q使得P和Q相乘的结果最好地拟合已知的评分，那么未知的评分也就可以用P的某一行乘上Q的某一列得到了：

这是预测用户u对商品i的评分，它等于P矩阵的第u行乘上Q矩阵的第i列。这个是最基本的SVD算法，那么如何通过已知评分训练得到P和Q的具体数值呢？

假设已知的评分为$r_{ui}$,则真实值与预测值的误差为：

继而可以计算出总的误差平方和：

接下来利用梯度下降法把SSE降到最小，那么P、Q就能最好地拟合R了。

这就是basic SVD。可以目标函数中只有训练误差，就很容易导致过拟合问题。因此，引入两个隐语义矩阵的正则项，得到RSVD:

2.2 RSVD的改进

于用户对商品的打分不仅取决于用户和商品间的某种关系，还取决于用户和商品独有的性质，我们希望将这些性质用基线评分(baseline estimates)来表示。

例如，我们希望得到小明对电影《泰坦尼克号》的评分，首先我们得到所有电影的评分均值$\mu$为3.7分。然后，我们得知该电影非常好看，评分可能比平均分高0.5.另外，小明是一个非常苛刻的观众，评分可能比平均分低0.3.我们得到小明对电影《泰坦尼克号》的基线评分3.7+0.5-0.3=3.9分。

定义用户u对物品i的评分 rui 的基线评分 bui :

bui=μ+bu+bi

其中 bu 和 bi 用户u和物品i的观测误差（独特属性）。

Koren将SVD的预测公式改成这样：

第一项为总的平均分，bu为用户u的属性值，bi为商品i的属性值，加入的这两个变量在SSE式子中同样需要惩罚，那么SSE就变成了下面这样：

2.3 ASVD

全称叫Asymmetric-SVD，即非对称SVD，其预测式子为

R(u)表示用户u评过分的商品集合，N(u)表示用户u浏览过但没有评过分的商品集合，Xj和Yj是商品的属性。这个模型很有意思，看预测式子，用户矩阵P已经被去掉了，取而代之的是利用用户评过分的商品和用户浏览过尚未评分的商品属性来表示用户属性，这有一定的合理性，因为用户的行为记录本身就能反应用户的喜好。而且，这个模型可以带来一个很大的好处，一个商场或者网站的用户数成千上万甚至过亿，存储用户属性的二维矩阵会占用巨大的存储空间，而商品数却没有那么多，所以这个模型的好处显而易见。但是它有个缺点，就是迭代时间太长了，这是可以预见的，以时间换空间嘛。
目标函数：

其中的向量z：

2.4 SVD++

引入隐式反馈，使用用户的历史浏览数据、用户历史评分数据、电影的历史浏览数据、电影的历史评分数据等作为新的参数。

隐含的反馈可以是打分动作（谁对某个商品打过分），或者是浏览记录等。 只要有类似的隐含反馈，客观上也表示了user对某个item的偏好。 毕竟，user不会无缘无故地浏览一个item，肯定有什么原因， 比如user喜欢紫色，恰恰这个item也是紫色的，那通过隐含回馈就可以对user对紫色的偏好建模出来。

现实中，隐含回馈的原因比较复杂，专门给一部分参数空间去建模，每个item对应一个向量 yi ，通过user隐含回馈过的item的集合来刻画用户的偏好。

SVD++的预测式子为

N(u) 用户u行为记录（包括浏览的和评过分的商品集合），是收缩因子取集合大小的根号是一个经验公式，并没有理论依据。
目标函数为：

minq∗,q∗,b∗,y∗∑(u,i)∈K(rui−μ−bi−bu−qTi(pu+|N(u)|−12∑j∈N(u)yj))2+λ1(||qi||2+||pu||2+∑j∈N(u)||yj||2)+λ2(b2u+bi2)

2.5 求解方法

基于梯度下降（为了并行，注意这里是批量梯度下降，不是随机梯度下降）方法，对目标学习公式求偏导，可得到如下迭代公式(为了方便源码表达，这里系数名称和源码保持一致):

bu←bu+∑i∈N(u)γ1(eui−γ6∗bu)

bi←bi+∑u∈N(i)γ1(eui−γ6∗bi)

qi←qi+∑u∈N(i)γ2(eui(pu+|N(u)|−12∑j∈N(u)yj)−γ7∗qi)

pu←pu+∑i∈N(u)γ2(eui∗qi−γ7∗pu)

yi←yi+∑u∈N(i)γ2(eui∗|N(u)|−12∗qi−γ7∗yi)

[1] Yehuda Koren 大牛的论文： Factorization Meets the Neighborhood: a Multifaceted Collaborative Filtering Model

[2]CSDN博主陈靖_非常的详细公式求解，但是文字解释太少了SVD在推荐系统中的应用详解以及算法推导

[3]协同过滤算法的几篇文章PFM/svd/ svd++

[4] SVD与SVD++

[5]推荐系统之协同过滤（CF）算法详解和实现

[6]Spark SVDPlusPlus 源码分析

拓展阅读：【推荐系统】特征值分解（谱分解）和奇异值分解（SVD），即在PCA上的应用