【MachineLearning】之 逻辑回归(Python 实现)
使用逻辑回归完成分类任务。
一、 步骤
(1)加载数据集
# !wget http://labfile.oss.aliyuncs.com/courses/1081/course-8-data.csv
import pandas as pd
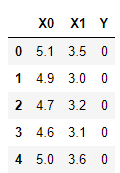
df = pd.read_csv("course-8-data.csv", header=0) # 加载数据集
df.head() # 预览前 5 行数据(2)绘制图像
from matplotlib import pyplot as plt
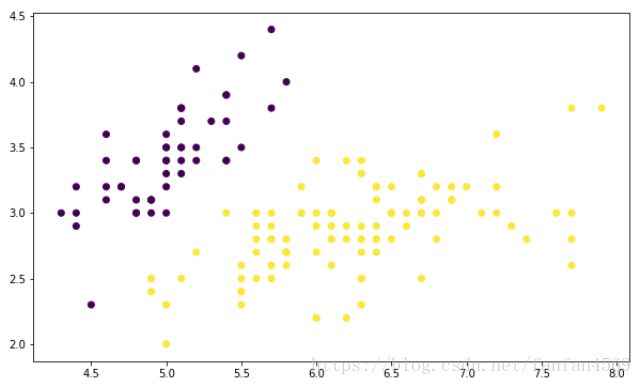
plt.figure(figsize=(10, 6))
plt.scatter(df['X0'],df['X1'], c=df['Y'])(3)逻辑回归函数定义
- Sigmoid 函数
- 损失函数
- 梯度计算
"""逻辑回归完整实现
"""
# Sigmoid 分布函数
def sigmoid(z):
sigmoid = 1 / (1 + np.exp(-z))
return sigmoid
# 损失函数
def loss(h, y):
loss = (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
return loss
# 梯度计算
def gradient(X, h, y):
gradient = np.dot(X.T, (h - y)) / y.shape[0]
return gradient
# 逻辑回归过程
def Logistic_Regression(x, y, lr, num_iter):
intercept = np.ones((x.shape[0], 1)) # 初始化截距为 1
x = np.concatenate((intercept, x), axis=1)
w = np.zeros(x.shape[1]) # 初始化参数为 0
for i in range(num_iter): # 梯度下降迭代
z = np.dot(x, w) # 线性函数
h = sigmoid(z) # sigmoid 函数
g = gradient(x, h, y) # 计算梯度
w -= lr * g # 通过学习率 lr 计算步长并执行梯度下降
z = np.dot(x, w) # 更新参数到原线性函数中
h = sigmoid(z) # 计算 sigmoid 函数值
l = loss(h, y) # 计算损失函数值
return l, w # 返回迭代后的梯度和参数(4)设置参数并训练得到结果
"""设置参数并训练得到结果
"""
import numpy as np
x = df[['X0','X1']].values
y = df['Y'].values
lr = 0.001 # 学习率
num_iter = 10000 # 迭代次数
# 训练
L = Logistic_Regression(x, y, lr, num_iter)
LOutput:
![]()
根据我们计算得到的权重,分类边界线的函数为:
y=L[1][0]+L[1][1]∗x1+L[1][2]∗x2 y = L [ 1 ] [ 0 ] + L [ 1 ] [ 1 ] ∗ x 1 + L [ 1 ] [ 2 ] ∗ x 2
* L[∗][∗] L [ ∗ ] [ ∗ ] 是从 L L 数组中选择相应取值
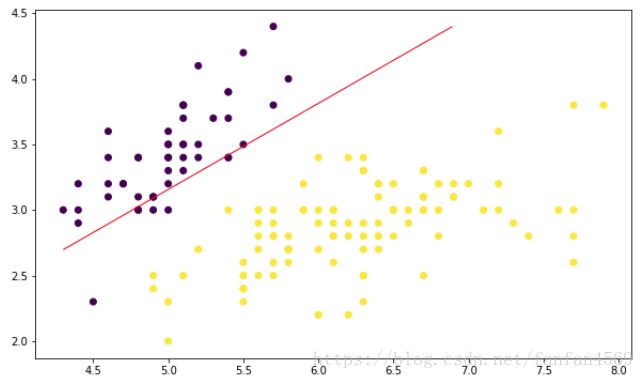
(5)绘制结果图
"""将上方得到的结果绘制成图
"""
plt.figure(figsize=(10, 6))
plt.scatter(df['X0'],df['X1'], c=df['Y'])
x1_min, x1_max = df['X0'].min(), df['X0'].max(),
x2_min, x2_max = df['X1'].min(), df['X1'].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = (np.dot(grid, np.array([L[1][1:3]]).T) + L[1][0]).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, levels=[0], linewidths=1, colors='red');
(6)递归下降后的结果
"""绘制损失函数变化曲线
"""
def Logistic_Regression(x, y, lr, num_iter):
intercept = np.ones((x.shape[0], 1)) # 初始化截距为 1
x = np.concatenate((intercept, x), axis=1)
w = np.zeros(x.shape[1]) # 初始化参数为 1
l_list = [] # 保存损失函数值
for i in range(num_iter): # 梯度下降迭代
z = np.dot(x, w) # 线性函数
h = sigmoid(z) # sigmoid 函数
g = gradient(x, h, y) # 计算梯度
w -= lr * g # 通过学习率 lr 计算步长并执行梯度下降
z = np.dot(x, w) # 更新参数到原线性函数中
h = sigmoid(z) # 计算 sigmoid 函数值
l = loss(h, y) # 计算损失函数值
l_list.append(l)
return l_list
lr = 0.01 # 学习率
num_iter = 30000 # 迭代次数
l_y = Logistic_Regression(x, y, lr, num_iter) # 训练
# 绘图
plt.figure(figsize=(10, 6))
plt.plot([i for i in range(len(l_y))], l_y)
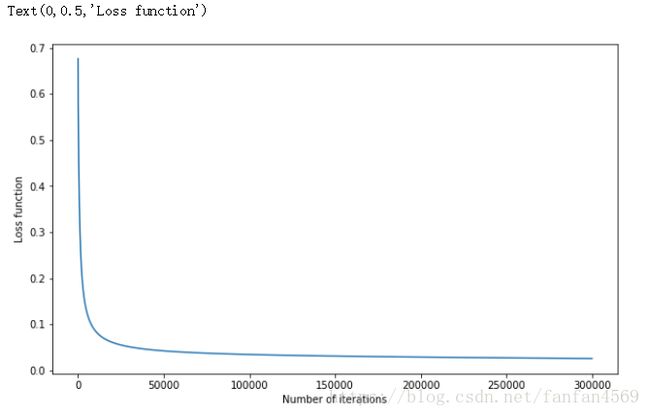
plt.xlabel("Number of iterations")
plt.ylabel("Loss function")发现迭代到 20000 次之后,数据趋于稳定,也就接近于损失函数的极小值。