NLMS算法简介及基于NLMS的时域EC实现

首先附上两篇感觉不错的博客：

点击打开链接  回声消除NLMS算法详解 

点击打开链接  NLMS算法 

点击打开链接 自适应滤波：最小均方误差滤波器（LMS、NLMS）

这三篇文章都很不错，所以重复的部分我都一笔带过，说下我自己的见解。

首先，LMS其实就是线性预测的知识，用过去的几点数据来预测当前的数据点。如果已知想要的期望信号就可以根据误差来逐步的逼近期望信号。

LMS用于线性预测的逼近步长固定的，NLMS是可变的，由于我们通常使用的LMS算法的迭代公式是建立在假定瞬时值代替期望值。所以输入信号

的大小对算法就会存在影响，能量大的地方就梯度大，能量小的地方就梯度小，这样会造成如果输入信号较小时候，收敛速度过慢，将输入信号按

照自身能量进行归一化，这样是 NLMS了。他们的区别也仅此而已，NLMS算法的一个应用是回声消除。利用webrtc中就是使用的该算法进行回声

消除的，但是webrtc中采用的是频域的回声消除算法。我们下面会用NLMS做一个时域的回声消除算法。该方法分远端信号和近端信号，我们通过

远端的信号来估计近端的回声，从而消除它，

一下附一些博客中关于NLMS的精华部分和我的matlab代码：

LMS原理及推导

LMS是时间换空间的应用，如果迭代步长过大，仍然有不收敛的问题；如果迭代步长过小，对于不平稳信号，还没有实现寻优就又引入了新的误差，屋漏偏逢连夜雨！所以LMS系统是脆弱的，信号尽量平稳、哪怕短时平稳也凑合呢。

给出框图：

关于随机梯度下降，可以参考之前的文章。这里直接给出定义式：

利用梯度下降：

                                                                          

 NLMS算法原理

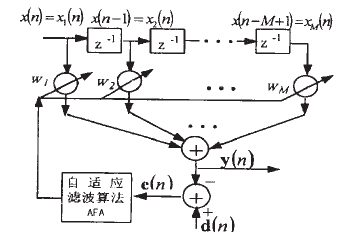
        回声消除系统基本结构如图1所示。

                        

                                                 图1  回声消除系统基本结构

        设置自适应滤波器系数w的所有初始值为0，即w(0) = 0，其长度为M。对输入信号进行采样，每次迭代取M个数据进行处理，输入矢量为

                        x(n) = [x₁(n) x₂(n) … x_M(n)]^T = [x(n)x(n-1) … x(n-M+1)]^T

        加权矢量为

                        w = [w₁ w₂… w₃]

        系统输出y(n)为

                        y(n) = wx(n)

        y(n)相对于期望信号d(n)的误差为

                        e(n) = d(n) – y(n) = d(n) -wx(n)             （黑色加粗部分是矢量，非加粗部分是标量）

        运用最小均方误差准则，就是求使得E[|e(n)|^2]最小时的w，因为是通过对其求导并令其等于0求得的，而|e(n)|在最小点不可导，所以使用的是|e(n)|^2。对于LMS算法，其滤波器系数迭代公式为

                        w(n+1) = w(n) + 2µe(n)x(n)

其中µ是步长因子，0 < µ < 1/ x^T(n)x(n)，在LMS算法中其值是固定的，因而收敛速度较慢。

        在LMS的基础上，用可变的步长因子代替固定的步长因子，就得到了NLMS算法，其迭代方程为

                        w(n+1) = w(n) + µ(n)e(n)x(n)=w(n) +ηe(n)x(n)/(δ+x^T(n)x(n))

其中η是修正的步长常量，0 < η < 2，δ为一个较小的整数，一般取0.0001，防止输入数据矢量x(n)的内积过小使得µ(n)过大而引起稳定性能下降。NLMS算法的收敛速度较快，效果较LMS算法好。

以下是代码部分：不想打字了，直接上图片

function main()
    x= audioread('speaker.wav');
    d= audioread('micin.wav');
    figure(1)
    subplot(311)
    plot(x);
    dd=d;
    res=EC(x,dd,q);%注意已经对齐了数据
    figure(1)
    subplot(311)
    plot(x);
    title('x');
    axis([1,length(x),-1,1]);
    subplot(312)
    plot(d);
    title('d');
    axis([1,length(d),-1,1]);
    subplot(313)
    plot(res);
    title('res');
    axis([1,length(res),-1,1]);
    aduiowrite('out.wav',res,16000);
end
%NLMS算法的EC应用
%x是远端
%d是近端
%q是滤波器阶次
function res= EC(x,d,q)
    len = length(x);
    w = zeros(1,q);
    res = d;
    mu = 1; q=64;
    for k = q:len-q+1
        if(k<=length(d))
          x_old = x(k-q+1:k);
          tmp= w*x_old;
          e=d(k)-tmp;
          w=w+x_old*e*mu/(x_old'*x_old+0.0001);
          if abs(d(k))>abs(e)  %不能大于原来的信号
              res(k)  = e;
          end
        end
    end
end