人工神经元网络

引言

• LaTeX不熟练多为图片。
• 图片多为SWUST模式识别课程李小霞老师课件。

一般的神经网络是由一层一层堆叠而成的，但是每层究竟在做啥呢？
数学公式$Y=f(W\ast X+b)$其中$Y$是输出量，$X$是输入量，$f()$是一个激活函数，$W$是权重矩阵，$b$是偏置向量。每一层都是通过该公式简单的得到输出$Y$。

数学理解
通过如下5种对输入空间（输入向量的集合）的操作，完成输入空间到输出空间的变换(矩阵的行空间到列空间)。 注：用“空间”二字是指被分类的并不是单个事物，而是一类事物。空间是指这类事物所有个体的集合。

1. 升维/降维
2. 放大/缩小
3. 旋转
4. 平移
5. “弯曲”
   这5种操作中，$1,2,3$的操作由 $W\ast X$完成的，$4$的操作是由$+b$完成的，$5$的操作则是由$f()$来实现。
   

1、前馈（forward）网络

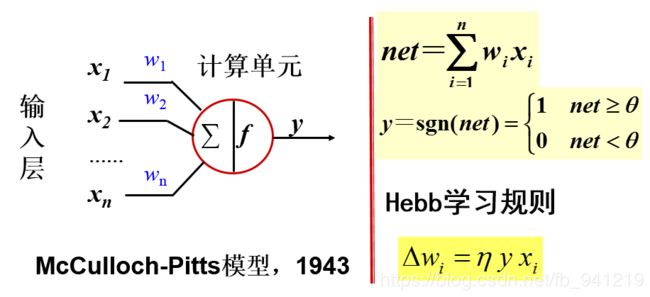
与线性分类器的关系

• 线性分类器$$g(x)=w^{T}x+w_0=w_1{x}_1+w_2{x}_2+...+w_0$$
• 感知器模型$$y=sgn(\sum _{i=1}^n{w}_i-\theta )$$
• 自学习，逐步修正，优化。
• 感知器学习算法（perceptron）
  (1)初始化
  (2)迭代$w(t)=\{\begin{array}{l}w(t-1)分对\\ w(t-1)+\eta y(t)x(t)分错\end{array}$
  $$\eta ：控制收敛速度的参数$$
• 局限：两类样本，线性分类。

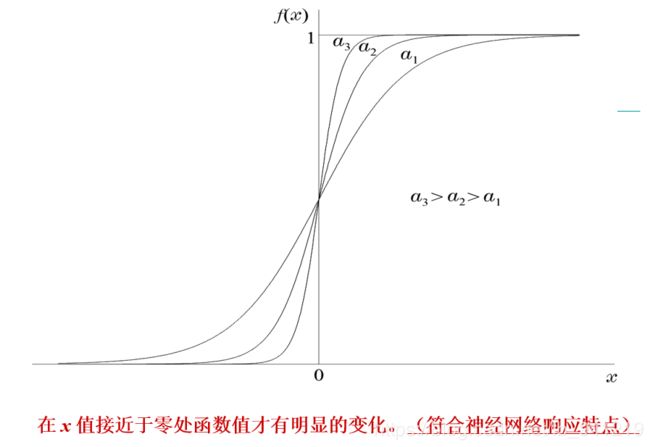
激活函数$f$为连续（可微）

$f$   #$不换行公式$   $$换行公式$$

$$f(x)=\frac{1}{1+e^{-ax}}$$

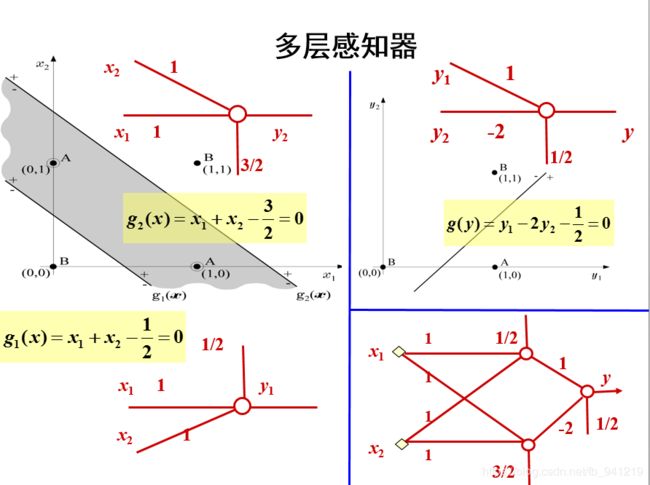
2、多层感知器(Multi-Layer Perceptron,MLP)

异或问题（XOR）的解决

单层感知器无法解决“异或”问题

![

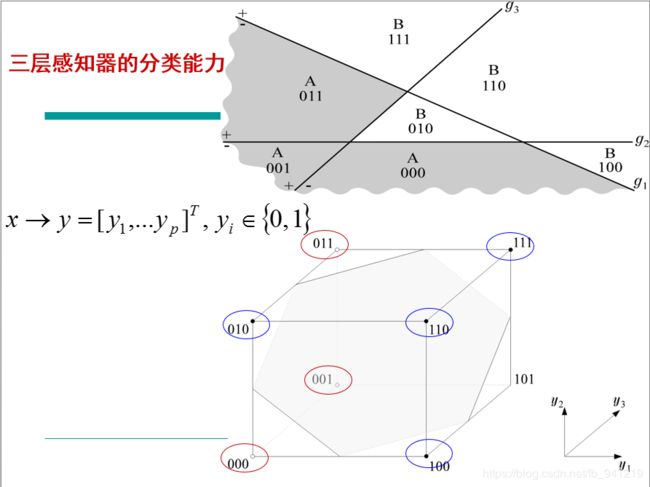
3、反向传播算法

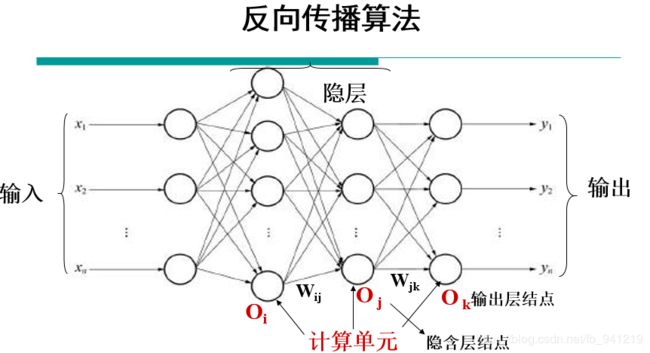
记住利用误差更新权重$w_{ij}$时是反向更新的，所以，所有的$△w_{ij}$的更新都可以用这两类来归纳：
（1）节点$j$是输出单元；
（2）节点$j$是隐含层单元，因为是逆向回传计算，因此在计算隐含层单元时，该隐含层的下一层已经计算完成。
一定要想象数据在网络中流动的动态过程，数据是怎样一步一步的过五关斩六将脑袋里面过一遍，会发现数据量是很庞大的。
误差传播迭代公式：

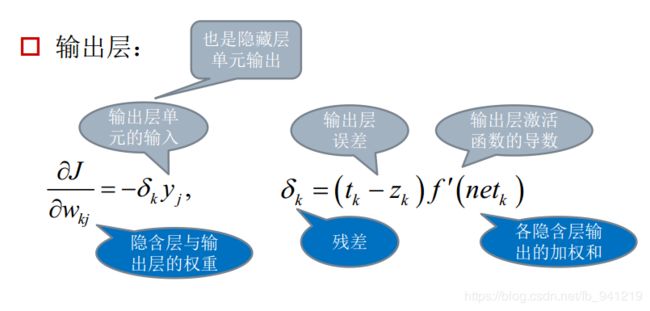
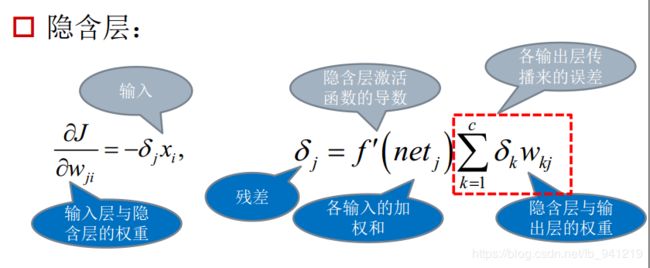
输出层和隐藏层的误差传播公式可统一为：
$$权重增量=-1\ast 学习步长\ast 目标函数对权重的偏导数$$$$目标函数对权重的偏导数=-1\ast 残差\ast 当前层的输入$$$$残差=当前层激励函数的导数\ast 上层反传来的误差$$$$上层反传来的误差=上层残差的加权和$$

为什么是负梯度修正：

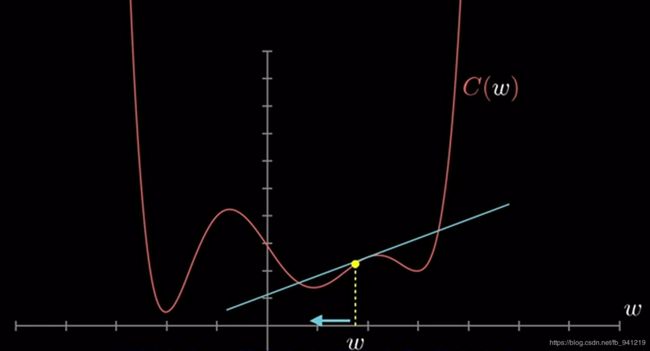
4、BP算法步骤

(1)选定权系数初始值。如0, rand(-0.3,0.3)
(2)重复下述过程直至收敛(对各样本依次计算)
①从前向后计算各层各单元$O_j$ $$ne{t}_j=\sum _i{w}_{ij}{O}_i{O}_j=1/(1+e^{-ne{t}_j})$$②对输出层计算局部梯度$${\delta }_j=(y-O_j)O_j(1-O_j)$$③从后向前计算各隐层$${\delta }_j=O_j(1-O_j)\sum _k{\delta }_k{w}_{jk}$$④计算并保存各权值修正量$$△w_{ij}(t)=\alpha △w_{ij}(t-1)+\eta {\delta }_j{O}_i$$⑤修正权值$$w_{ij}(t+1)=w_{ij}(t)+△w_{ij}(t)$$

其中，$sigmoid$函数取$$f(x)=\frac{1}{1+e^{-x}}$$故 $$f^{\prime }\left(x\right)=O_j(1-O_j)$$
代入$f(x)$对应上面的公式就很好理解了。一般的，$\eta =0.1\sim 3\alpha =0\sim 1,常用0.95.$

5、多样本

优化方法总结参考1 参考2 参考3 参考4
2d classification with 2-layer neural network demo参考5

6、典型的机器学习步骤

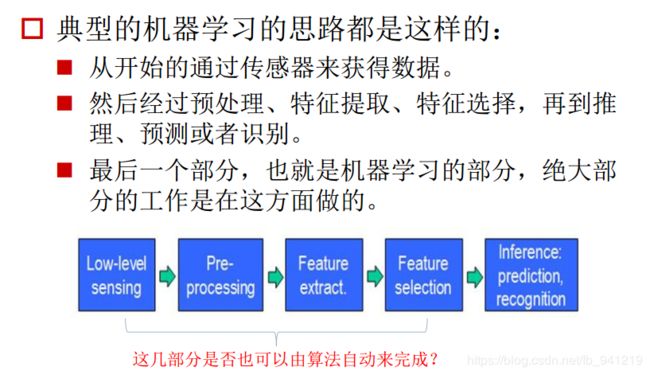
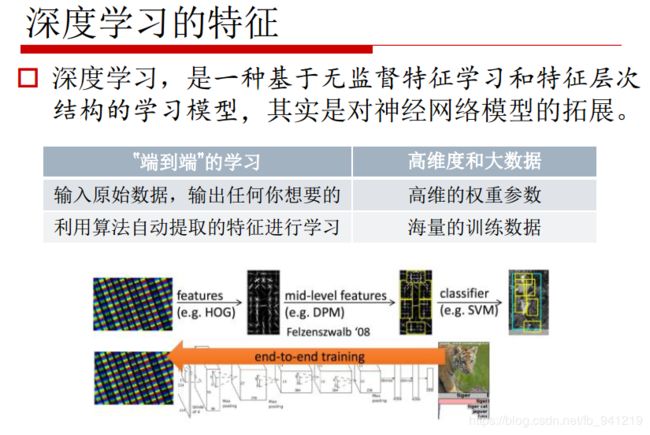
7、深度学习与神经网络的区别

附录

李小霞老师教学代码，严格按照公式推导过程码出来的。对理解推导过程很有帮助。

%严格按照BP网络计算公式来设计的一个matlab程序,对BP网络进行了优化设计
%优化1：设计了yyy，即在o(k)计算公式时，当网络进入平坦区时(<0.0001)学习率加大，  出来后学习率又还原 P68 3.30
%优化2：v(i,j)=v(i,j)+deltv(i,j)+a*dv(i,j); 参照了P67 3.29

clear all
clc
inputNums=3;              %输入层节点
outputNums=3;             %输出层节点
hideNums=10;              %隐层节点数
maxcount=20000;           %最大迭代次数
samplenum=3;              %一个计数器，无意义
precision=0.001;          %预设精度
yyy=1.3;                  %yyy是帮助网络加速走出平坦区 

alpha=0.01;                %学习率设定值
a=0.5;                    %BP优化算法的一个设定值，对上组训练的调整值按比例修改
error=zeros(1,maxcount+1);  %error数组初始化；目的是预分配内存空间
errorp=zeros(1,samplenum);%同上

v=rand(inputNums,hideNums);      %3*10;v初始化为一个3*10的随机归一矩阵; v表输入层到隐层的权值
deltv=zeros(inputNums,hideNums); %3*10;内存空间预分配
dv=zeros(inputNums,hideNums);    %3*10;  


w=rand(hideNums,outputNums);     %10*3;同V
deltw=zeros(hideNums,outputNums);%10*3
dw=zeros(hideNums,outputNums);   %10*3


samplelist=[0.1323,0.323,-0.132;0.321,0.2434,0.456;-0.6546,-0.3242,0.3255];  %3*3;指定输入值3*3(实为3个向量)
expectlist=[0.5435,0.422,-0.642;0.1,0.562,0.5675;-0.6464,-0.756,0.11];  %3*3;期望输出值3*3(实为3个向量)，有导师的监督学习

count=1;
while (count<=maxcount)          %结束条件1迭代2000次
    c=1;
    while (c<=samplenum)
      for k=1:outputNums 
        d(k)=expectlist(c,k);    %获得期望输出的向量,d(1:3)表示一个期望向量内 的值
      end
    
      for i=1:inputNums
        x(i)=samplelist(c,i);    %获得输入的向量（数据）,x(1:3)表一个训练向量
      end

%Forward();
     for j=1:hideNums
         net=0.0;
           for i=1:inputNums
               net=net+x(i)*v(i,j);%输入层到隐层的加权和∑X(i)V(i)               3.11
           end
         y(j)=1/(1+exp(-net));     %输出层处理f(x)=1/(1+exp(-x))单极性sigmiod函数 3.14
     end
     for k=1:outputNums
         net=0.0;
         for j=1:hideNums
             net=net+y(j)*w(j,k);
         end
         if count>=2&&error(count)-error(count+1)<=0.0001
            o(k)=1/(1+exp(-net)/yyy);
         else o(k)=1/(1+exp(-net));     %同上
         end
     end

%BpError(c)反馈/修改;
    errortmp=0.0;
    for k=1:outputNums
        errortmp=errortmp+(d(k)-o(k))^2;  %第一组训练后的误差计算
    end
    errorp(c)=0.5*errortmp;               %误差E=∑(d(k)-o(k))^2 * 1/2      3.15
%end
      
      %Backward();
    for k=1:outputNums
        yitao(k)=(d(k)-o(k))*o(k)*(1-o(k)); %输入层误差偏导                  3.25a
    end
    for j=1:hideNums
        tem=0.0;
        for k=1:outputNums
            tem=tem+yitao(k)*w(j,k);         %为了求隐层偏导，而计算的∑
        end
         yitay(j)=tem*y(j)*(1-y(j));         %隐层偏导                      3.25b
     end

   %调整各层权值
   for j=1:hideNums
       for k=1:outputNums
           deltw(j,k)=alpha*yitao(k)*y(j);    %权值w的调整量deltw(已乘学习率)3.26a
           w(j,k)=w(j,k)+deltw(j,k)+a*dw(j,k);%权值调整，这里的dw=dletw(t-1)，实际是对BP算法的一个
           dw(j,k)=deltw(j,k);                %改进措施--增加动量项目的是提高训练速度          
       end                                                                 %3.29
   end
   for i=1:inputNums
       for j=1:hideNums
           deltv(i,j)=alpha*yitay(j)*x(i);     %同上deltw
           v(i,j)=v(i,j)+deltv(i,j)+a*dv(i,j); 
           dv(i,j)=deltv(i,j);
       end
   end
    c=c+1;
    end%第二个while结束；表示一次BP训练结束
    
    double tmp;
    tmp=0.0;
    for i=1:samplenum
      tmp=tmp+errorp(i)*errorp(i);%误差求和
    end
    tmp=tmp/c;
    error(count)=sqrt(tmp);%误差求均方根,即精度

    if (error(count)

$$比心♡！$$