图像特征与描述(1)
图像特征与描述(1)
- 引言
- 1、颜色特征
- 2、几何特征:边缘
- 3、基于关键点的特征描述子
- 4、几何特征:关键点
- 5、几何特征:Harris角点
- 6、FAST角点检测
- 7、几何特征: 斑点
- 8、局部特征:SIFT
- 9、代码实践
- Harris
- FAST
- Blob
- SIFT
引言
笔记总结。python+opencv_tutorial、CPP+opencv_tutorial
1、颜色特征
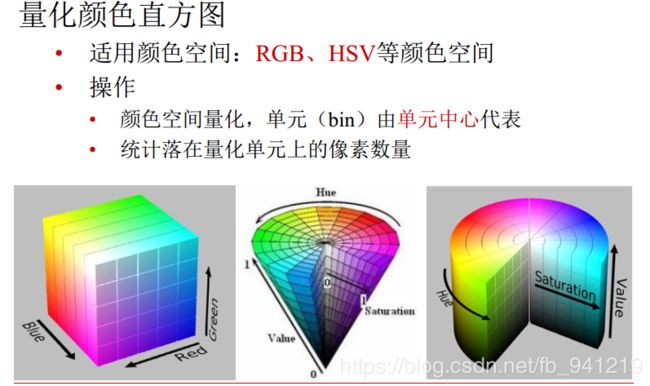



设想两幅图像的颜色直方图几乎相同, 只是互相错开了一个bin, 这时如果采用L1距离或者欧拉距离计算两者的相似度, 会得到很小的相似度值。
为了克服这个缺陷, 需要考虑到相似但不相同的颜色之间的相似度:
- 一种方法是采用二次式距离。
- 另一种方法是对颜色直方图事先进行平滑过滤,即每个bin中的像素对于相邻的几个bin也有贡献。
2、几何特征:边缘

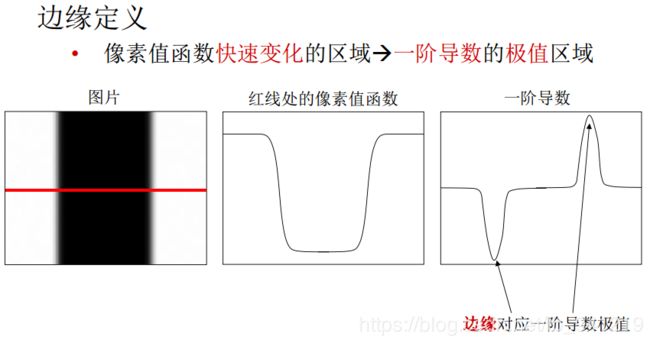
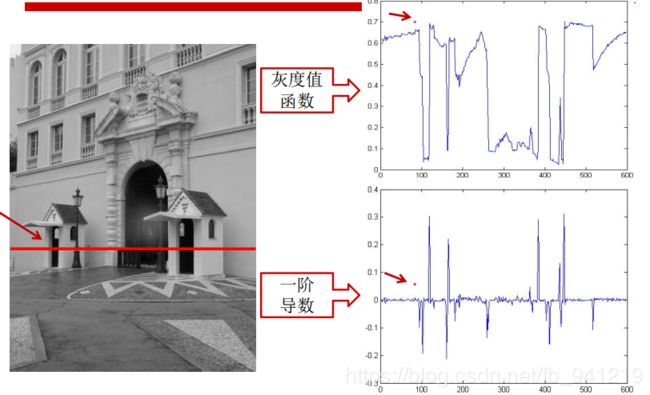
一阶导数的极值点就是边缘。
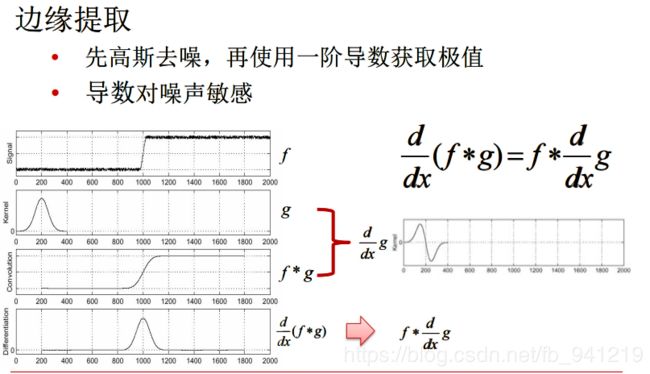
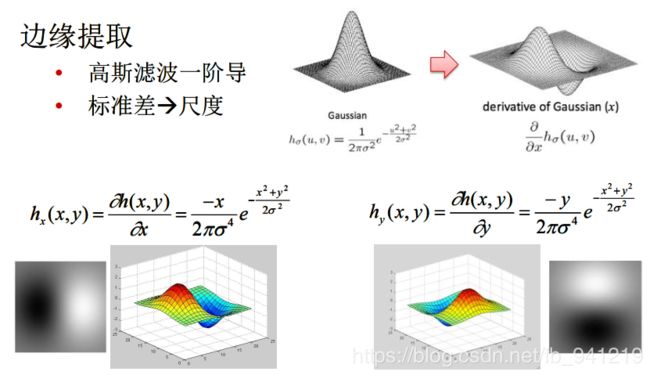

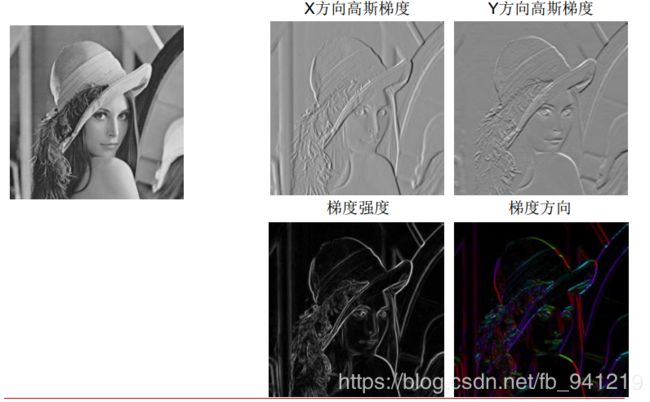
两个方向求导数,再联立起来。
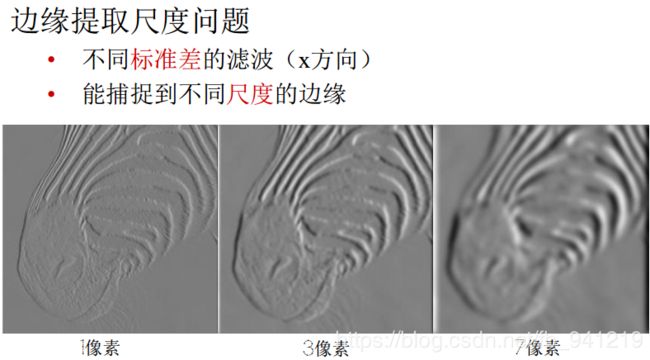
高斯函数的 σ \sigma σ取不同值
3、基于关键点的特征描述子
从不同的距离, 不同的方向、 角度, 不同的光照条件下观察一个物体时, 物体的大小,形状, 明暗都会有所不同。 但我们依然可以判断它是同一件物体。
理想的特征描述子应该具备这些性质。 即,在大小、 方向、 明暗不同的图像中, 同一特征点应具有足够相似的描述子, 称之为描述子的可复现性。
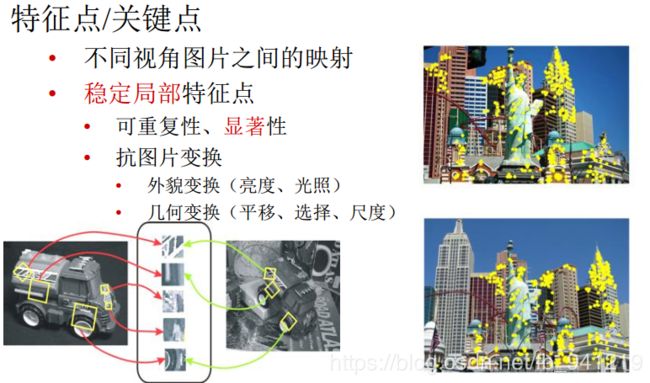
4、几何特征:关键点

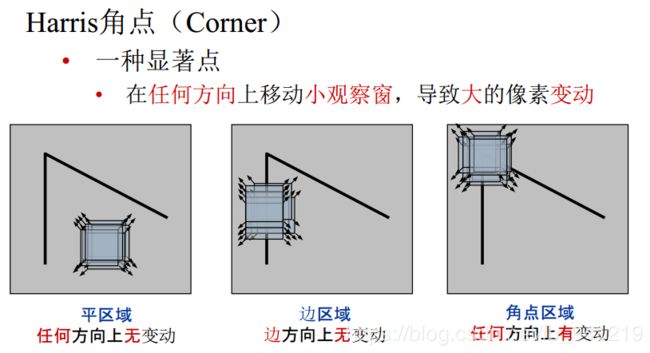
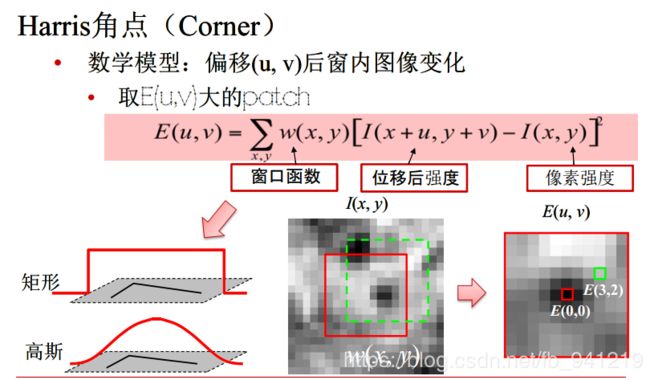
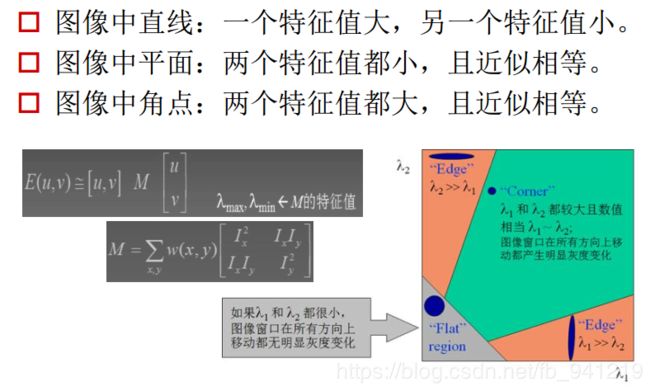
5、几何特征:Harris角点

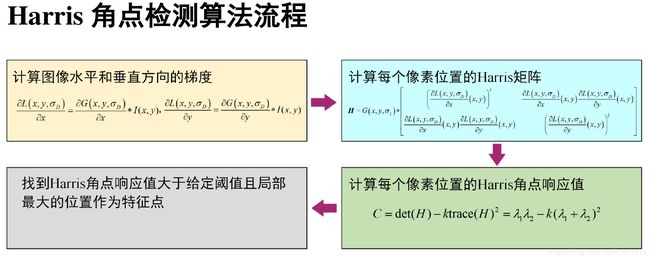
Harris角点参考
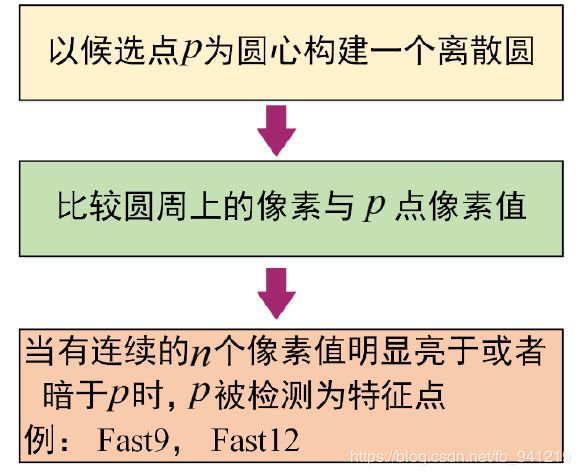
6、FAST角点检测
- F A S T FAST FAST 角点检测是一种的快速角点特征检测算法。
- F A S T FAST FAST 角点定义为: 若某像素点与其周围领域内足够多的像素点处于不同的区域, 则该像素点可能为角点, 也就是某些属性与众不同。
- F A S T FAST FAST特征点检测是对兴趣点所在圆周上的16个像素点进行判断, 若判断后的当前中心像素点为暗或亮, 将决定其是否为角点。
- 确定一个阈值 t t t, 观察某像素点为中心的一个半径等于3像素的离散化的圆, 这个圆的边界上有16个像素。
- 如果在这个大小为16个像素的圆上有n(一般是12个点)个连续的像素点, 它们的像素值要么都比 I p + t {I}_{p}+t Ip+t 大, 要么都比 I p − t {I}_{p}-t Ip−t 小, 则p它就是一个角点。
FAST具体计算过程:
- 从图片中选取一个像素点P,下面我们将判断它是否是一个特征点。我们首先把它的密度(即灰度值)设为 I p Ip Ip。
- 设定一个合适的阙值t :当2个点的灰度值之差的绝对值大于t时,我们认为这2个点不相同。
- 考虑该像素点周围的16个像素。
- 现在如果这16个点中有连续的n个点都和点不同,那么它就是一个角点。 这里n设定为12。
- 我们现在提出一个高效的测试,来快速排除一大部分非特征点的点。该测试仅仅检查在位置1、9、5和13四个位置的像素(首先检查1和9,看它们是否和点相同。如果是,再检查5和13)。如果是一个角点,那么上述四个像素点中至少有3个应该和点相同。如果都不满足,那么不可能是一个角点。

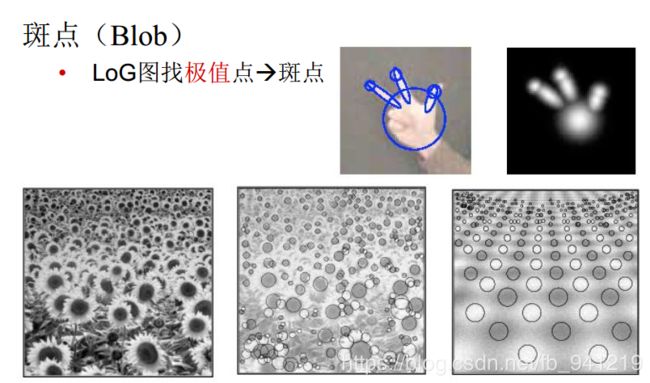
7、几何特征: 斑点
斑点:二阶导数取最大值最小值的地方!
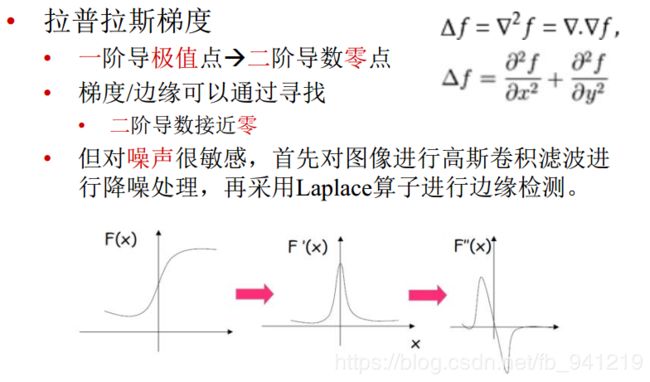
两阶两个方向的导数相加,但对噪声很敏感, 首先对图像进行高斯卷积滤波进行降噪处理, 再采用Laplace算子进行边缘检测 : L a p l a c i a n o f G a u s s i a n ( L o G ) \quad:Laplacian of Gaussian (LoG) :LaplacianofGaussian(LoG)当 σ \,\sigma\, σ较小时, 将识别出更为细节的边缘。

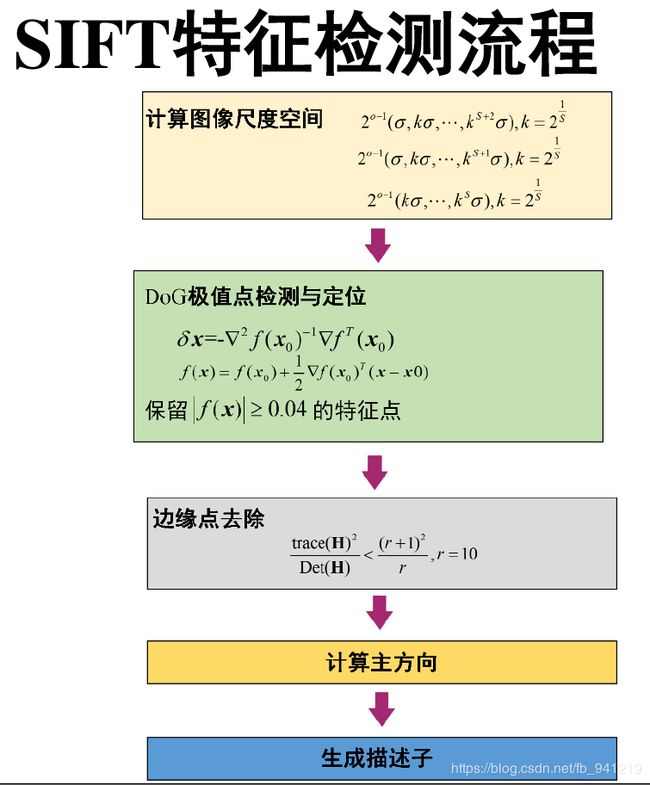
8、局部特征:SIFT
图像尺度空间:
平时生活中,用人眼去看一张照片时,随着观测距离的增加,图像会逐渐变得模糊。那么计算机在“看”一张照片时,会从不同的“尺度”去观测照片,尺度越大,图像越模糊。
那么这里的“尺度”就是二维高斯函数当中的σ值,一张照片与二维高斯函数卷积后得到很多张不同σ值的高斯图像,这就好比你用人眼从不同距离去观测那张照片。所有不同尺度下的图像,构成单个原始图像的尺度空间。“图像尺度空间表达”就是图像在所有尺度下的描述。
尺度是自然客观存在的,不是主观创造的。高斯卷积只是表现尺度空间的一种形式。
基于尺度空间不变的特征
- 特点:
• 具有良好的不变性
- - • 旋转、 尺度缩放、 平移、 亮度变化、
- - • 对视角变化、 仿射变换和噪声也有一定程度的稳定性
• 独特性好, 信息量丰富: 适用于在海量特征数据库中进行快速、 准确的匹配
• 多量性:即使少数物体也可以产生大量SIFT特征
• 计算快: 经优化的SIFT匹配算法甚至可以达到实时性
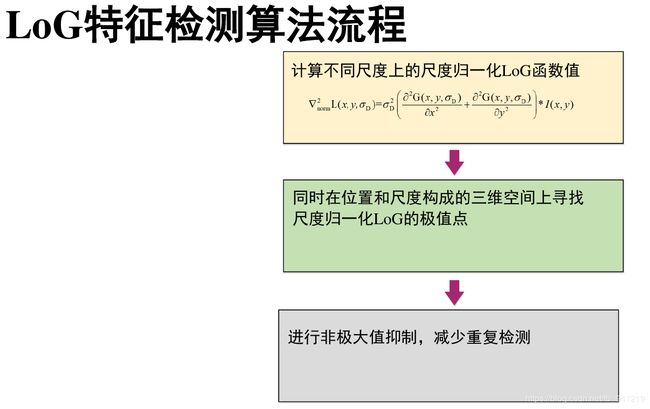
SIFT特征计算步骤
- 在 D o G DoG DoG尺度空间中获取极值点, 即关键点
• L o G LoG LoG尺度空间和 D o G DoG DoG尺度空间 ( 高 斯 差 分 D O G − D i f f e r e n c e o f G a u s s ) (高斯差分DOG - Difference of Gauss) (高斯差分DOG−DifferenceofGauss) - 对关键点处理
• 位置插值(获得精确的关键点)
• 去除边缘点 - 关键点的方向估计
- 关键点描述子的生成
• 区域坐标旋转
• 计算采样区域的直方图
高斯尺度空间 ( G S S − G a u s s S c a l e S p a c e ) : (GSS - Gauss Scale Space): (GSS−GaussScaleSpace):
唯一能产生尺度空间的核为高斯核函数,在低通滤波中,高斯平滑滤波无论是时域还是频域都十分有效。高斯函数具有五个重要性质:
(1)二维高斯具有旋转对称性;
(2)高斯函数是单值函数;
(3)高斯函数的傅立叶变换频谱是单瓣的;
(4)高斯滤波器宽度(决定着平滑程度)是由参数σ表征的,而且σ和平滑程度的关系是非常简单的;
(5)二维高斯滤波的计算量随滤波模板宽度成线性增长而不是成平方增长。
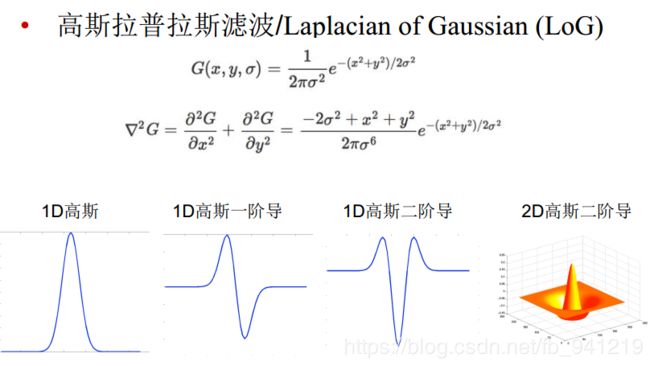
所以我们将图像的尺度空间表示成一个函数 L ( x , y , σ ) L(x,y,σ) L(x,y,σ),它是由一个变尺度的高斯函数 G ( x , y , σ ) G(x,y,σ) G(x,y,σ)与图像 I ( x , y ) I(x,y) I(x,y)卷积产生的。即
L ( x , y , σ ) = G ( x , y , σ ) ∗ I ( x , y ) L(x, y, σ) = G(x, y, σ) ∗ I(x, y) L(x,y,σ)=G(x,y,σ)∗I(x,y)其中 ∗ * ∗代表卷积操作,$G(x, y, σ) $为二维高斯核函数,表示为: G ( x , y , σ ) = 1 2 π σ 2 e − ( x 2 + y 2 ) / 2 σ 2 G(x,y,\sigma) = \frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2} G(x,y,σ)=2πσ21e−(x2+y2)/2σ2
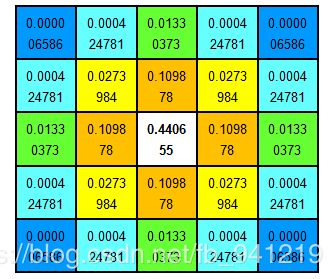
高 斯 核 高斯核 高斯核
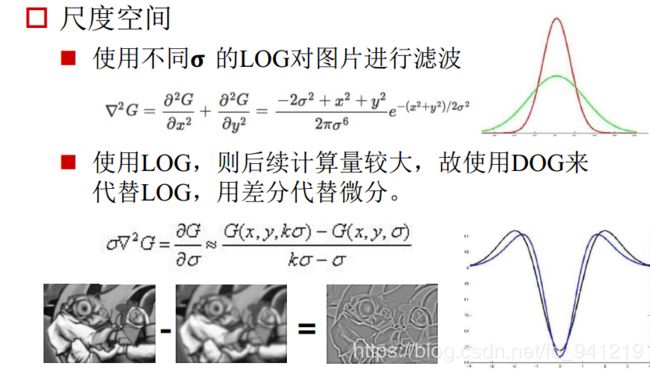
高斯差分 ( D O G − D i f f e r e n c e o f G a u s s ) : (DOG - Difference of Gauss): (DOG−DifferenceofGauss):
S I F T SIFT SIFT算法建议,在某一尺度上对特征点的检测,可以通过对两个相邻高斯尺度空间的图像相减,得到一个 D o G ( D i f f e r e n c e o f G a u s s i a n s ) DoG (Difference of Gaussians) DoG(DifferenceofGaussians)的响应值图像 D ( x , y , σ ) D(x,y,σ) D(x,y,σ)。然后,仿照 L o G LoG LoG方法,通过对响应值图像 D ( x , y , σ ) D(x,y,σ) D(x,y,σ)进行非最大值抑制(局部极大搜索,正最大和负最大),在位置空间和尺度空间中定位特征点。其中 D ( x , y , σ ) = ( G ( x , y , k σ ) − G ( x , y , σ ) ) ∗ I ( x , y ) = L ( x , y , k σ ) − L ( x , y , σ ) D(x, y, σ) = (G(x, y, kσ) − G(x, y, σ)) ∗ I(x, y) = L(x, y, kσ) − L(x, y, σ) D(x,y,σ)=(G(x,y,kσ)−G(x,y,σ))∗I(x,y)=L(x,y,kσ)−L(x,y,σ)式中, k k k为相邻尺度空间倍数的常数。
为什么用 D O G DOG DOG来检测特征点:
L i n d e b e r g Lindeberg Lindeberg证明用 σ 2 σ^2 σ2标准化的高斯拉普拉斯 ( ∇ 2 G , L O G , L a p l a c i a n o f G a u s s ) (∇^2G, LOG, Laplacian of Gauss) (∇2G,LOG,LaplacianofGauss)有着真正的尺度无关的特性,而 M i k o l a j c z y k Mikolajczyk Mikolajczyk发现,相比于其他一系列函数(比如梯度, H e s s i a n Hessian Hessian, H a r r i s Harris Harris角点函数等),用 σ 2 σ^2 σ2标准化的高斯拉普拉斯 ( σ 2 ∇ 2 G ) (σ^2∇^2G) (σ2∇2G)有着更稳定的图像特征,因此 σ 2 ∇ 2 G σ^2∇^2G σ2∇2G函数是我们理想的寻找特征点的函数。而在此,我们利用 D o G DoG DoG来近似 σ 2 ∇ 2 G σ^2∇^2G σ2∇2G。
通过热传导方程也可以帮助我们理解 D o G DoG DoG与 σ 2 ∇ 2 G σ^2∇^2G σ2∇2G之间的近似关系。由热传导方程可知(通常用 t = σ 2 t=σ^2 t=σ2): ∂ G ∂ σ = σ ∇ 2 G \frac{\partial G}{\partial \sigma} =\sigma \nabla^2G ∂σ∂G=σ∇2G使用 L O G LOG LOG, 则后续计算量较大, 故使用 D O G DOG DOG来代替 L O G LOG LOG, 用差分代替微分. σ ∇ 2 G = ∂ G ∂ σ ≈ G ( x , y , k σ ) − G ( x , y , σ ) k σ − σ \sigma { \nabla }^{ 2 }G =\frac { \partial G }{ \partial \sigma } \approx \frac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma} σ∇2G=∂σ∂G≈kσ−σG(x,y,kσ)−G(x,y,σ)
因此:
D o G = G ( x , y , k σ ) − G ( x , y , σ ) ≈ ( k − 1 ) σ 2 ∇ 2 G DoG = G(x, y, kσ) − G(x, y, σ) ≈ (k − 1)σ^2∇^2G DoG=G(x,y,kσ)−G(x,y,σ)≈(k−1)σ2∇2G
而常数项(k - 1)并不会影响极值的位置。所以 D o G DoG DoG是 σ 2 ∇ 2 G σ^2∇^2G σ2∇2G的近似。
对于使用 D o G DoG DoG来近似 σ 2 ∇ 2 G σ^2∇^2G σ2∇2G,有如下优点:
( 1 ) σ 2 ∇ 2 G (1)σ^2∇^2G (1)σ2∇2G需要使用两个方向的高斯二阶微分卷积核,而 D o G DoG DoG直接使用高斯卷积核,省去了对卷积核的生成的运算量。
( 2 ) D o G (2)DoG (2)DoG保留了各个高斯尺度空间的图像,这样,在生成某一空间尺度的特征时,可以直接尺度空间图像,而无需重新再次生成该尺度的图像。
高斯核性质及其在 S I F T SIFT SIFT中的应用:
对于二维高斯卷积,有如下性质:
1、距离高斯核中心 3 σ 3σ 3σ距离外的系数很小,相对于 3 σ 3σ 3σ内的系数值可以忽略不计,所以只用 ( 6 σ + 1 ) ∗ ( 6 σ + 1 ) (6σ + 1)*(6σ + 1) (6σ+1)∗(6σ+1)的面积计算卷积即可。
2、线性可分,二维高斯核卷积(计算次数 O ( n 2 ∗ M ∗ N ) O(n2*M*N) O(n2∗M∗N))效果等于水平和竖直方向的两个一维高斯核 ( 计 算 次 数 O ( n ∗ M ∗ N ) + O ( n ∗ M ∗ N ) ) ) (计算次数O(n*M*N) + O(n*M*N))) (计算次数O(n∗M∗N)+O(n∗M∗N)))累积处理的效果。 n ∗ n n*n n∗n为滤波器大小, M ∗ N M*N M∗N图像大小。
3、对一幅图像进行多次连续高斯模糊的效果与一次更大的高斯模糊可以产生同样的效果,大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。例如,使用半径分别为 6 和 8 的两次高斯模糊变换得到的效果等同于一次半径为 10 (勾股定理)的高斯模糊效果。根据这个关系,使用多个连续较小的高斯模糊处理不会比单个高斯较大处理时间要少。
其中,性质3有助我们更快速的生成 G S S GSS GSS。虽然两个小半径处理时间并不会比单个高斯较大半径处理的时间少,但相对于原图像,我们已经有一个小半径模糊过的图像,即可用另一小半径在现成的图像上进行模糊得到较大半径的模糊效果。例如尺度为 σ 0 σ_0 σ0的图像已经存在,我们要得到尺度为 k σ 0 kσ_0 kσ0的图像,即可只使用尺度为 [ ( k σ 0 ) 2 − ( σ 0 ) 2 ] 1 / 2 [(kσ_0)^2-(σ_0)^2]^{1/2} [(kσ0)2−(σ0)2]1/2的核在尺度为 σ 0 σ_0 σ0的图像上进行模糊,即可得到尺度为 k σ 0 kσ_0 kσ0模糊的图像,同理可得到高斯尺度空间各层的图像,使得高斯尺度空间生产得更快。
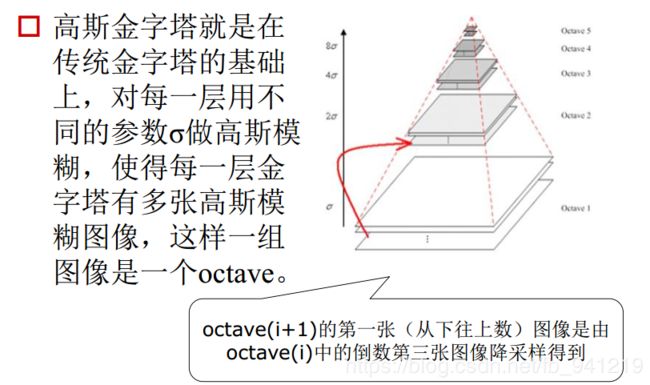
高斯参数 σ \,\sigma\, σ越来越大。
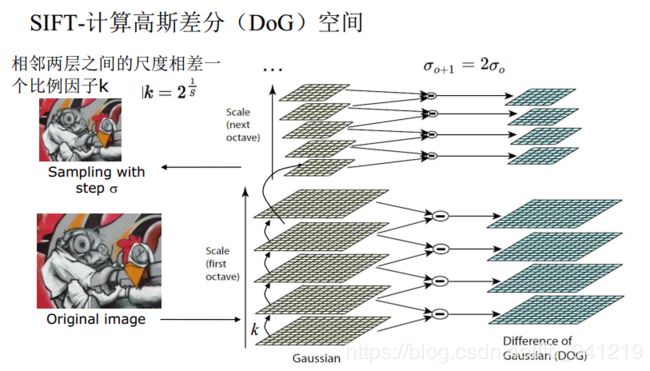
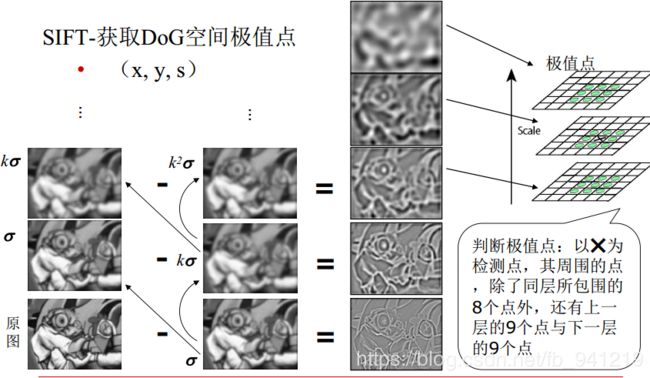

亚像素(精确度更高的像素位置) :
D O G : DOG: DOG:
D ( x , y , σ ) = ( G ( x , y , k σ ) − G ( x , y , σ ) ) ∗ I ( x , y ) = L ( x , y , k σ ) − L ( x , y , σ ) D(x, y, σ) = (G(x, y, kσ) − G(x, y, σ)) ∗ I(x, y) = L(x, y, kσ) − L(x, y, σ) D(x,y,σ)=(G(x,y,kσ)−G(x,y,σ))∗I(x,y)=L(x,y,kσ)−L(x,y,σ)

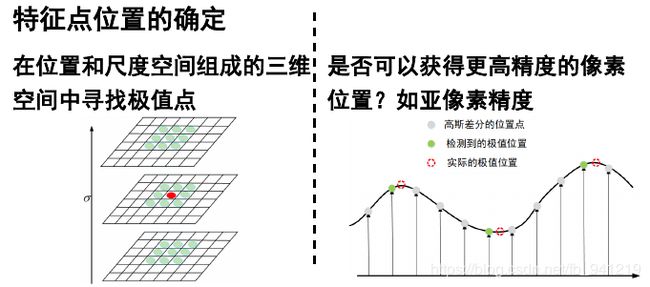

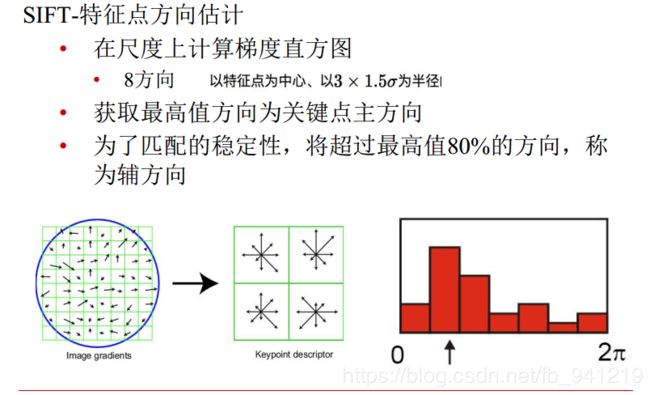
每一个点都有自己的梯度方向,然后再做统计。
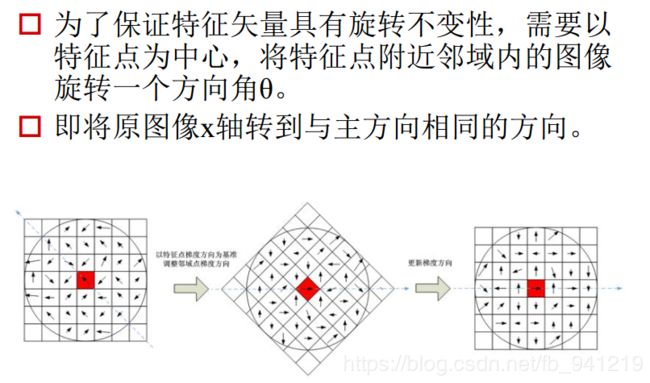
为了保证特征矢量具有旋转不变性, 需要以特征点为中心, 将特征点附近邻域内的图像旋转一个方向角θ。
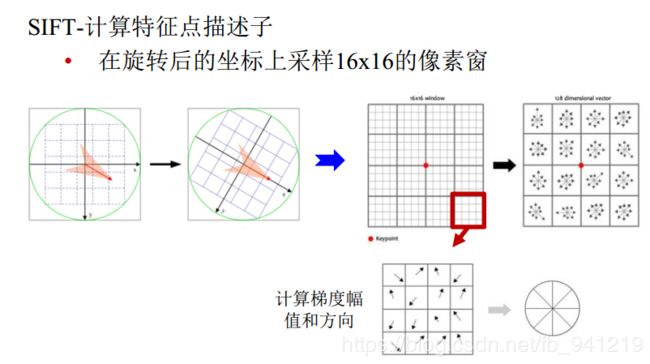
最后一个图就是,对16个格子求主方向,组成一个向量,这个向量就是这个点基于主方向的他的临近区域的特征描述。
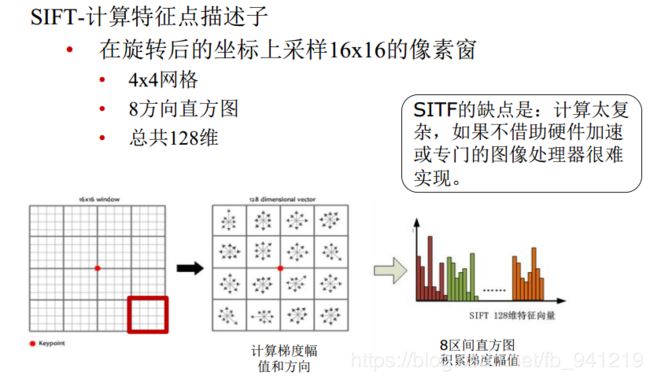
SITF的缺点是: 计算太复杂, 如果不借助硬件加速或专门的图像处理器很难实现。sift参考
9、代码实践
Harris
Harris角点
import numpy as np
import cv2 as cv
filename = 'test_1.jpg'
img = cv.imread(filename)
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
gray = np.float32(gray)
dst = cv.cornerHarris(gray,2,3,0.04)
#result is dilated for marking the corners, not important
dst = cv.dilate(dst,None)
# Threshold for an optimal value, it may vary depending on the image.
img[dst>0.01*dst.max()]=[0,0,255]
cv.imshow('dst',img)
if cv.waitKey(0) & 0xff == 27:
cv.destroyAllWindows()

FAST
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img = cv.imread('test_1.jpg',0)
# Initiate FAST object with default values
fast = cv.FastFeatureDetector_create()
# find and draw the keypoints
kp = fast.detect(img,None)
img2 = cv.drawKeypoints(img, kp, None, color=(255,0,0))
# Print all default params
print( "Threshold: {}".format(fast.getThreshold()) )
print( "nonmaxSuppression:{}".format(fast.getNonmaxSuppression()) )
print( "neighborhood: {}".format(fast.getType()) )
print( "Total Keypoints with nonmaxSuppression: {}".format(len(kp)) )
cv.imwrite('fast_true.png',img2)
# Disable nonmaxSuppression
fast.setNonmaxSuppression(0)
kp = fast.detect(img,None)
print( "Total Keypoints without nonmaxSuppression: {}".format(len(kp)) )
img3 = cv.drawKeypoints(img, kp, None, color=(255,0,0))
cv.imwrite('fast_false.png',img3)
cv.imshow('fastResult',img3)
cv.waitKey(0)
cv.destroyAllWindows()

Blob
斑点原教程有一句错误:
detector = cv2.SimpleBlobDetector()===>detector = cv2.SimpleBlobDetector_create()
# Standard imports
import cv2
import numpy as np;
# Read image
im = cv2.imread("test_2.jpg", cv2.IMREAD_GRAYSCALE)
cv2.imshow("src",im)
# Set up the detector with default parameters.
detector = cv2.SimpleBlobDetector_create()
# Detect blobs.
keypoints = detector.detect(im)
# Draw detected blobs as red circles.
# cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS ensures the size of the circle corresponds to the size of blob
im_with_keypoints = cv2.drawKeypoints(im, keypoints, np.array([]), (0, 0, 255),
cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
# Show keypoints
cv2.imshow("Keypoints", im_with_keypoints)
cv2.waitKey(0)
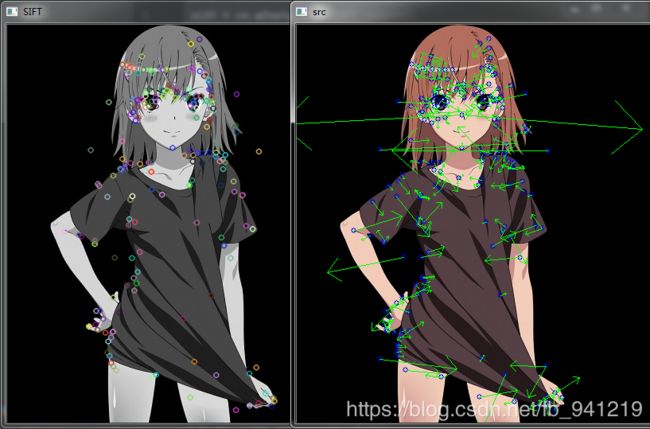
SIFT
参考sift源码,一步一步按照公式写的代码。

python+opencv,编译错误解决方案参考。
sift = cv.xfeatures2d.SIFT_create()
cv2.error: OpenCV(3.4.3) C:\projects\opencv-python\opencv_contrib\modules\xfeatures2d\src\sift.cpp:1207: error: (-213:The function/feature is not implemented) This algorithm is patented and is excluded in this configuration; Set OPENCV_ENABLE_NONFREE CMake option and rebuild the library in function ‘cv::xfeatures2d::SIFT::create’
import numpy as np
import cv2 as cv
img = cv.imread('test_1.jpg')
gray = cv.cvtColor(img,cv.COLOR_BGR2GRAY)
sift = cv.xfeatures2d.SIFT_create()
kp = sift.detect(gray,None)
img=cv.drawKeypoints(gray,kp,img)
cv.imshow("SIFT", img)
cv.imwrite('sift_keypoints.jpg',img)
cv.waitKey(0)
cv.destroyAllWindows()

可以看到C++源码和python+opencv结果没多大区别,几乎一样,但是python+opencv的速度比C++源码快很多。