Dijkstra算法求无向带权图最短路径——Java

Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

Dijkstra算法采用的是贪心算法的策略，在整个算法过程中一直要维护两个表，这两个表分别表示尚未遍历的结点和已遍历的结点。大概过程如下：

1. 声明两个集合，open和close，open用于存储未遍历的节点，close用来存储已遍历的节点；
2. 初始阶段，将初始节点放入close，其他所有节点放入open；
3. 以初始节点为中心向外一层层遍历，获取离指定节点最近的子节点放入close并从新计算路径，直至close包含所有子节点。

我在Intellij IDEA中实现了此算法，与BFS算法一样，首先我们需要构建一个图进行测试。在这里，我构建如下图：

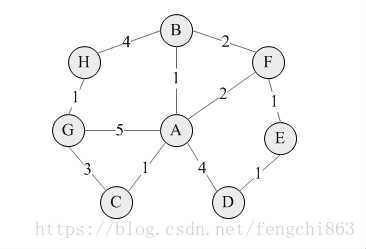
以下为构建代码，首先创建Node对象用于封装图中的vertex结点信息，它包括结点的名字和子结点，子结点就是与之相邻的所有结点。

public class Node {
    private String name;
    private Map child=new HashMap<>();
    public Node(String name){
        this.name=name;
    }
    public String getName() {
        return name;
    }
    public void setName(String name) {
        this.name = name;
    }
    public Map getChild() {
        return child;
    }
    public void setChild(Map child) {
        this.child = child;
    }
}

其中自动生成了constructor、getter和setter方法，方便进行结点操作。

MapBuilder用于初始化数据源，返回图的起始节点。

public class MapBuilder {
    public Node build(Set open, Set close){
        Node nodeA=new Node("A");
        Node nodeB=new Node("B");
        Node nodeC=new Node("C");
        Node nodeD=new Node("D");
        Node nodeE=new Node("E");
        Node nodeF=new Node("F");
        Node nodeG=new Node("G");
        Node nodeH=new Node("H");
        nodeA.getChild().put(nodeB, 1);
        nodeA.getChild().put(nodeC, 1);
        nodeA.getChild().put(nodeD, 4);
        nodeA.getChild().put(nodeG, 5);
        nodeA.getChild().put(nodeF, 2);
        nodeB.getChild().put(nodeA, 1);
        nodeB.getChild().put(nodeF, 2);
        nodeB.getChild().put(nodeH, 4);
        nodeC.getChild().put(nodeA, 1);
        nodeC.getChild().put(nodeG, 3);
        nodeD.getChild().put(nodeA, 4);
        nodeD.getChild().put(nodeE, 1);
        nodeE.getChild().put(nodeD, 1);
        nodeE.getChild().put(nodeF, 1);
        nodeF.getChild().put(nodeE, 1);
        nodeF.getChild().put(nodeB, 2);
        nodeF.getChild().put(nodeA, 2);
        nodeG.getChild().put(nodeC, 3);
        nodeG.getChild().put(nodeA, 5);
        nodeG.getChild().put(nodeH, 1);
        nodeH.getChild().put(nodeB, 4);
        nodeH.getChild().put(nodeG, 1);
        open.add(nodeB);
        open.add(nodeC);
        open.add(nodeD);
        open.add(nodeE);
        open.add(nodeF);
        open.add(nodeG);
        open.add(nodeH);
        close.add(nodeA);
        return nodeA;
    }
}

接下来是算法部分，Dijkstra类用于计算起始结点到所有其他结点的最短路径：

public class Dijkstra {
    Set open = new HashSet();
    Set close = new HashSet();
    Map path = new HashMap();//封装路径距离
    Map pathInfo = new HashMap();//封装路径信息

    public Node init() {
        //初始路径,因没有A->E这条路径,所以path(E)设置为Integer.MAX_VALUE
        path.put("B", 1);
        pathInfo.put("B", "A->B");
        path.put("C", 1);
        pathInfo.put("C", "A->C");
        path.put("D", 4);
        pathInfo.put("D", "A->D");
        path.put("E", Integer.MAX_VALUE);
        pathInfo.put("E", "A");
        path.put("F", 2);
        pathInfo.put("F", "A->F");
        path.put("G", 5);
        pathInfo.put("G", "A->G");
        path.put("H", Integer.MAX_VALUE);
        pathInfo.put("H", "A");
        //将初始节点放入close,其他节点放入open
        Node start = new MapBuilder().build(open, close);
        return start;
    }

    public void computePath(Node start) {
        //取距离start节点最近的子节点,放入close
        Node nearest = getShortestPath(start);
        if (nearest == null) {
            return;
        }
        close.add(nearest);     //已遍历的
        open.remove(nearest);   //未遍历的

        Map childs = nearest.getChild();
        for (Node child : childs.keySet()) {
            if (open.contains(child)) {//如果子节点在open中
                Integer newCompute = path.get(nearest.getName()) + childs.get(child);
                if (newCompute < path.get(child.getName())) {//新计算出来的距离小于之前设置的距离
                    path.put(child.getName(), newCompute);
                    pathInfo.put(child.getName(), pathInfo.get(nearest.getName()) + "->" + child.getName());
                }
            }
        }
        computePath(start);//重复执行自己,确保所有子节点被遍历
        computePath(nearest);//向外一层层递归,直至所有顶点被遍历
    }

    public void printPathInfo() {
        Set> pathInfos = pathInfo.entrySet();
        for (Map.Entry pathInfo : pathInfos) {
            System.out.println(pathInfo.getKey() + ":" + pathInfo.getValue());
        }
    }

    /**
     * 获取与node最近的子节点
     */
    private Node getShortestPath(Node node) {
        Node res = null;
        int minDis = Integer.MAX_VALUE;
        Map childs = node.getChild();
        // 遍历与Node相连接的所有节点，选取其中距离最短的节点
        for (Node child : childs.keySet()) {
            if (open.contains(child)) {
                int distance = childs.get(child);
                if (distance < minDis) {
                    minDis = distance;
                    res = child;
                }
            }
        }
        return res;
    }
}

然后我们构建了测试用例，如下：

public class DijkstraTest { 
    /**
    *
    * Method: getShortestPath(Node node)
    *
    */
    @Test
    public void testGetShortestPath() throws Exception {
        //TODO: Test goes here...
        Dijkstra test=new Dijkstra();
        Node start=test.init();
        test.computePath(start);
        test.printPathInfo();
    }
} 

运行结果如下：

D:A->D
E:A->F->E
F:A->F
G:A->C->G
B:A->B
C:A->C
H:A->B->H