之前的小结:https://blog.csdn.net/fufck/article/details/78844309
1.bzoj2301
题意:满足 a ≤ x ≤ b , c ≤ y ≤ d ,且gcd(x,y) = k 的个数(1≤n≤50000,1≤a≤b≤50000,1≤c≤d≤50000,1≤k≤50000)
思路:f(n)表示gcd恰好为n的个数,F(n)表示n|gcd的个数。

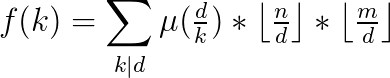
后面那个只有2根号n个取值
#include
#include
#include
#include
#include
#include
#include
#include
2.hdu5663
题意:求∑f(i,j)的值,当gcd(i,j)为完全平方数 f(i,j)=0;否则为1(1≤n,m≤10,000,000)
思路:f(n)表示gcd恰好为n*n的个数,F(n)表示n*n|gcd的个数。


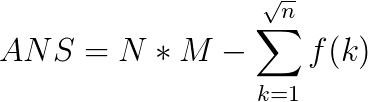
这样会超时,但是我们观察第二个式子,我们可以枚举d,前缀sum重新定义为∑u[k*k|d]
#include
#include
#include
#include
#include
#include
#include
#include
3.hdu6053
题意:两个序列,A,B,A序列给出,Bi<=Ai,问满足所有区间 gcd(bl,bl+1...br)≥2 B序列的方案数
思路:设G(i)表示i|gcd的个数
![G(d)=\prod_{i=1}^{n}\left \lfloor \frac{a[i]}{d} \right \rfloor](http://img.e-com-net.com/image/info8/b710f24ba32542239539cc35d248fd82.gif)
![ANS=\sum_{d=2}{}{-\mu(d)*\prod_{i=1}^{n}\left \lfloor \frac{a[i]}{d} \right \rfloor}](http://img.e-com-net.com/image/info8/0a79b415d81e42a58b1208f103cc2700.gif)
#include
#include
#include
#include
#include
#include
#include
#include
4.hdu1695
题意:求(1,b)区间和(1,d)区间里面gcd(x, y) = k的数的对数(1<=x<=b , 1<= y <= d)。(x,y) (y,x)是同一对
#include
#include
#include
#include
#include
#include
#include
#include
5.hdu5656
题意:给你一个集合,求所有子集的gcd之和
#include
#include
#include
#include
#include
#include
#include
#include

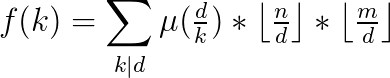


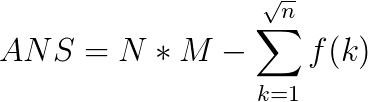
![G(d)=\prod_{i=1}^{n}\left \lfloor \frac{a[i]}{d} \right \rfloor](http://img.e-com-net.com/image/info8/b710f24ba32542239539cc35d248fd82.gif)
![ANS=\sum_{d=2}{}{-\mu(d)*\prod_{i=1}^{n}\left \lfloor \frac{a[i]}{d} \right \rfloor}](http://img.e-com-net.com/image/info8/0a79b415d81e42a58b1208f103cc2700.gif)