PyTorch学习笔记(11)——论nn.Conv2d中的反向传播实现过程

0. 前言

众所周知，反向传播（back propagation）算法 (Rumelhart et al., 1986c)，经常简称为backprop，它允许来自代价函数的信息通过网络向后流动，以便计算梯度。它是神经网络之所以可以进行学习的最根本因素。在如PyTorch、Tensorflow等深度学习框架中，都广泛的使用了自动微分（Autograd）的机制，主要也就是从哈佛的智能概率系统组（Harvard Intelligent Probabilistic Systems Group）的Autograd的基础上进行的[1]。

在PyTorch的1.0dev版发布之际，我将以ATen后端中对某一卷积层（二维卷积Conv2d）的weight和bias进行梯度求解、误差信号求解以及权重更新逻辑进行系统的梳理。

需要注意的是，这篇文章涉及的内容非常多，所以在一些地方可能会有疏忽或者纰漏，如果您发现了，请告知我进行更正，提前感谢一下本文的读者朋友们。

下面，正式开始PyTorch中的2维卷积层中weight和bias的梯度求解和权重更新的逻辑分析。

1. 提出问题

当你准备开始学习PyTorch后端的2维卷积的weight和bias的更新逻辑时，首先需要避免将时间浪费在无谓的寻找上，最好的方法是去官方论坛询问或者看看是否之前有人问过类似的问题。

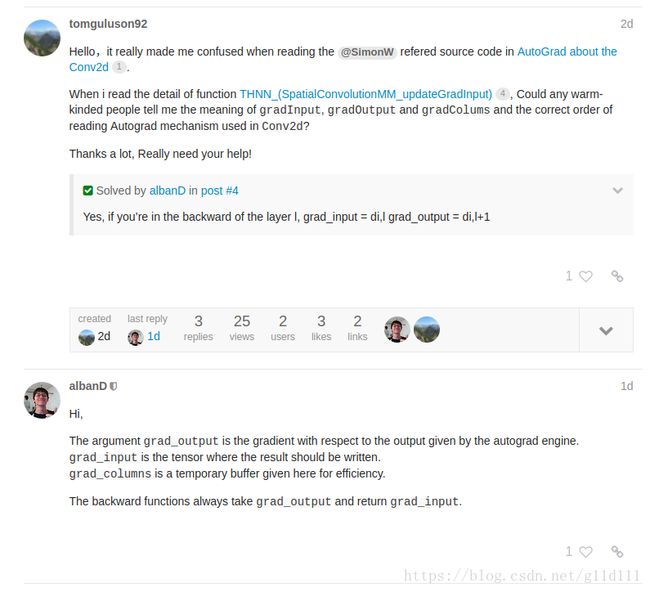
这里我就找到了一个论坛版主@SimonW 回复了这个问题 “AutoGrad about the Conv2d”[2]：

这里我只看了gpu cuda中的实现。其中有两个方法是这里要着重强调的内容，也就是pytorch/aten/src/THCUNN/generic/SpatialConvolutionMM.cu中的THNN_(SpatialConvolutionMM_updateGradInput)和
THNN_(SpatialConvolutionMM_accGradParameters)。

这里，先简明扼要的告诉大家这两个函数的作用：

• THNN_(SpatialConvolutionMM_updateGradInput)
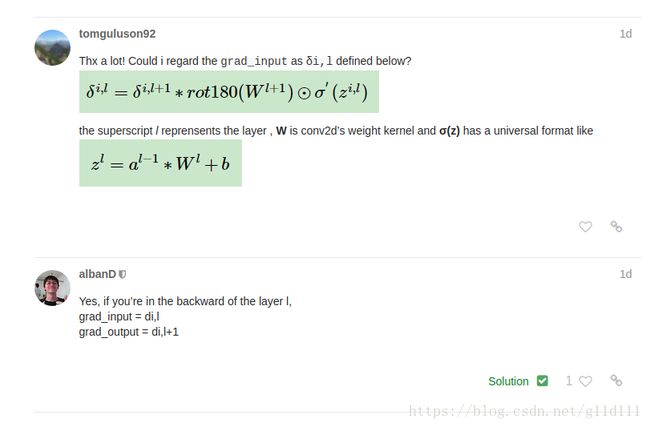
  xxx_updateGradInput的作用（比如当前要进行权值更新的卷积层为第$l$层）是根据第$l+1$层的误差信号${\delta }^{(i,l+1)}$(i表示当前Batch中的第i个样本)，求得当前层第$l$层的误差信号${\delta }^{(i,l)}$。

• THNN_(SpatialConvolutionMM_accGradParameters)
  xxx_accGradParameters的作用是求得需要更新权重的梯度，对2维卷积层，因为更新逻辑为：
  $$W^l=W^l-\alpha \sum _{i=1}^m{\delta }^{(i,l)}\ast rot180(a^{(i,l-1)})$$
  $$b^l=b^l-\alpha \sum _{i=1}^m\sum _{u,v}({\delta }^{(i,l)}{)}_{u,v}$$
  所以其输出为用于weight更新的$\alpha {\sum }_{i=1}^m{\delta }^{(i,l)}\ast rot180(a^{(i,l-1)})$和用于bias更新的$\alpha {\sum }_{i=1}^m{\sum }_{u,v}({\delta }^{(i,l)}{)}_{u,v}$。

ps：误差信号以及DNN、CNN的反向传播以及更新逻辑细节请看下面的第2部分《预备知识》。

2.预备知识

2.1 回顾DNN的反向传播算法[3]

在学习PyTorch中CNN反向传播中梯度和权重更新的内容时，在诸如GEMM、im2col等计算中的逻辑会让我觉的非常困惑。

通过分析发现，对于有必要先把DNN和CNN的反向传播的理论搞的非常清楚，再去阅读代码会效果更好更有针对性，以便于我们可以更清晰的理解这部分代码的设计逻辑。

DNN这个部分就比较简单了，
① 首先，误差信号${\delta }^l$的定义为：
$${\delta }^l=\frac{\partial J(\mathbf{W},b,x,y)}{\partial z^l}$$
其中，$J(\mathbf{W},b,x,y)$是神经网络的损失函数，$z^l={\mathbf{W}}^l\ast a^{l-1}+b^l$为未经过激活函数的值，
$a^l=\sigma (z^l)$为经过激活函数之后得到的值。

② 因为最后一层$L$（输出层）的误差信号容易求得：

设损失函数为
$$J(\mathbf{W},b,x,y)=\frac{1}{2}{\Vert \begin{array}{c}{a}^L-y\end{array}\Vert }_2^2$$
那么最后一层的误差信号根据前面的定义为
$${\delta }^L=\frac{\partial J(\mathbf{W},b,x,y)}{\partial z^L}=(a^L-y)\odot {\sigma }^{\prime }(z^L)$$
所以根据链式法则，前面任意一层的误差信号可求得为（设$L>l$）
$${\delta }^l=\frac{\partial J(\mathbf{W},b,x,y)}{\partial z^l}=\frac{\partial J(\mathbf{W},b,x,y)}{\partial z^L}\frac{\partial z^L}{\partial z^{L-1}}...\frac{\partial z^{l+1}}{\partial z^l}$$

所以，问题的变成：如何求$\partial z^{l+1}/\partial z^l$，根据前面的$z^l$和$a^l$的定义，可以容易的求得，这里不再展开了。

③ DNN中的weight和bias更新策略如下：

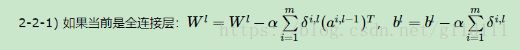
总结一下

2.2 回顾CNN的反向传播算法[3]

这部分主要是参考李建平博士的博客，这里不展开，只说结论：
因为在DNN中的${\delta }^{l+1}$和${\delta }^l$的递推关系在CNN中仍然成立：
$${\delta }^l=\frac{\partial J(\mathbf{W},b,x,y)}{\partial z^{l+1}}\frac{\partial z^{l+1}}{\partial z^l}={\delta }^{l+1}\frac{\partial z^{l+1}}{\partial z^l}$$
只不过，DNN（用于全连接层）和CNN（用于卷积层）的误差信号求解方式有一些改变

至于为什么让$W^{l+1}$ rot180，这个就需要看参考资料[3]，刘博士举了一个非常生动的例子便于理解。

最后，已知某卷积层的误差信号，根据下面的方式对卷积核的权重进行更新。

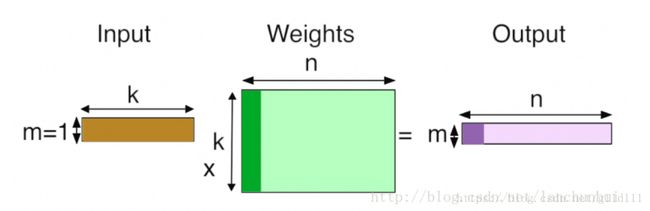
2.3 卷积操作中的矩阵乘法（gemm）[7]

2.3.1 全连接

k 个输入；
n 个神经元；
每个神经元都会学到一组权值向量，以和输入进行内积运算；
n 个输出；
2.3.2 卷积
卷积操作对于高维（多个平面）的输入，单个卷积核的深度应和输入的深度（depth）保持一致：

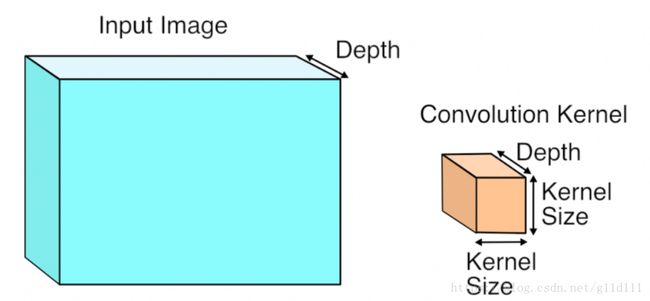
3 维卷积运算执行完毕，得一个 2 维的平面：

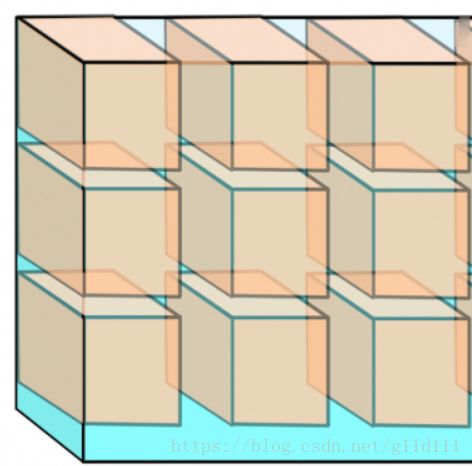
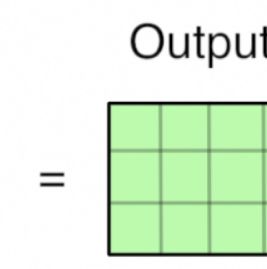
注，n 个3维卷积核以得到 n 个 feature maps；

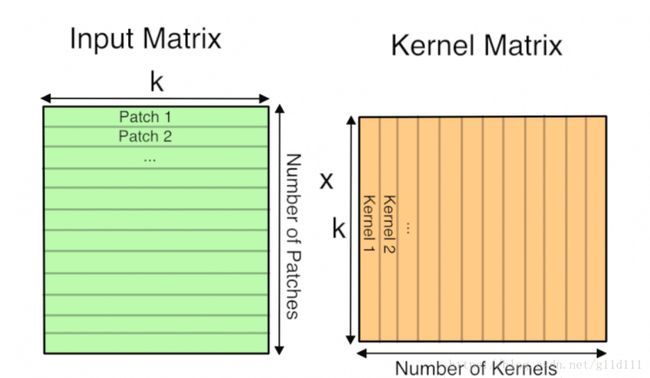
2.3.3 卷积操作中的矩阵乘法

• 按 [kernel_height, kernel_width, kernel_depth] ⇒ 将输入分成 3 维的 patch，并将其展成一维向量；
• 

• 此时的卷积操作就可转化为矩阵乘法：
  

3. GPU Cuda版的nn.Conv2d反向传播梯度更新策略分析

根据第1部分最后的内容，我们这里对这pytorch/aten/src/THCUNN/generic/SpatialConvolutionMM.cu中的THNN_(SpatialConvolutionMM_updateGradInput)和THNN_(SpatialConvolutionMM_accGradParameters)这两个文件进行仔细分析，中间涉及到的一些内容，会放在第2部分中。

3.1 THNN_(SpatialConvolutionMM_updateGradInput)

这两个方法大体类似，这里重点详细分析xxx_updateGradInput方法，剩下的xxx_accGradParameters就不展开说了。

1. 方法定义：
   

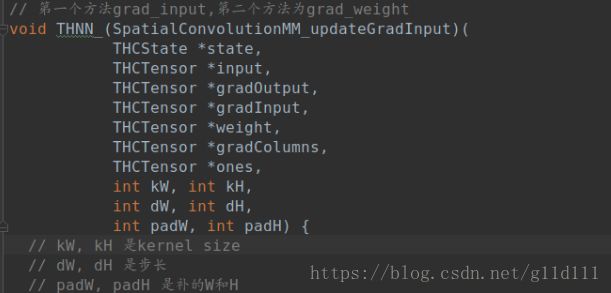
2. 部分参数说明：
   gradOutput是由autograd根据输出来求得的上一层$l$的当前层$l+1$的误差信号${\delta }^{l+1}$。
   gradInput是根据col2im_kernel设计的逻辑来将gradColumns的权重梯度进行汇总到grad_input中的操作，也就是存放当前层误差信号${\delta }^l$这个结果的地方。
   grad_columns是一个临时的buffer，为了效率，缓存weight（权值）的中间结果之用。
   input是输入卷积层的内容，这里按标准的二维卷积输入为N x C x H x W。
   weight是当前层也就是第$l+1$层的权重。
   ones 没用，为了对齐输入。
   kW, kH是卷积核的宽和高。
   dW, dH是宽和高的步长。
   padW和padH是padding的宽和高。

3. 代码分析：

void THNN_(SpatialConvolutionMM_updateGradInput)(
           THCState *state,
           THCTensor *input,
           THCTensor *gradOutput,
           THCTensor *gradInput,
           THCTensor *weight,
           THCTensor *gradColumns,
           THCTensor *ones,
           int kW, int kH,
           int dW, int dH,
           int padW, int padH) {
  // 以单张RGB图像为例 Batchsizex3xHxW
  THCUNN_assertSameGPU(state, 5, input, gradOutput, weight,
                       gradColumns, gradInput);
  THArgCheck(THCTensor_(isContiguous)(state, weight), 4,
             "weight tensor has to be contiguous");

  // weight的nDimension=2表示1维卷积
  // Params
  // weight -> size[1] 表示当前的feature map的个数, 这里为3
  // weight -> size[0] 表示经过conv后, feature map的个数,也就是卷积核的个数
  int nInputPlane = weight->nDimension == 2 ? weight->size[1]/(kW*kH) : weight->size[1];
  int nOutputPlane = weight->size[0];

  int freeWeight = 0;
  // 其weight->size[1] = 3,卷积kernel设置为10, 则weight->size[0]=10
  // 卷积核假定都取3x3
  // 0:新的feature map数/新channel数量
  // 1:旧的feature map数/旧channel数量
  // 2:kH 3:kW
  // 那么选取的例子中的weight为 10 x 3 x 3 x 3
  if (weight->nDimension == 4) {
    int64_t s1 = weight->size[0];
    int64_t s2 = weight->size[1] * weight->size[2] * weight->size[3];
    // 构建一个weight
    weight = THCTensor_(newWithStorage2d)(state, weight->storage, weight->storageOffset, s1, -1, s2, -1);
    freeWeight = 1;
  }
  // 检查
  THNN_(SpatialConvolutionMM_shapeCheck)
       (state, input, gradOutput, weight, NULL, kH, kW, dH, dW, padH, padW);

  // 重新构建一个连续的input和gradOutput
  input = THCTensor_(newContiguous)(state, input);
  gradOutput = THCTensor_(newContiguous)(state, gradOutput);
  int batch = 1;
  // input的nDimension为3, 表示输入的batchsize=1
  if (input->nDimension == 3) {
    // Force batch
    batch = 0;
    THCTensor_(resize4d)(state, input, 1, input->size[0], input->size[1], input->size[2]);
    THCTensor_(resize4d)(state, gradOutput, 1, gradOutput->size[0], gradOutput->size[1], gradOutput->size[2]);
  }

  // 图像输入和输出的大小
  // 例子中取padW = padH = 0, kW = kH = 3, dW = dH = 3 inputHeight = inputWidth = 9
  int64_t inputWidth   = input->size[3];
  int64_t inputHeight  = input->size[2];
  int64_t outputWidth  = (inputWidth + 2*padW - kW) / dW + 1;
  int64_t outputHeight = (inputHeight + 2*padH - kH) / dH + 1;

  // Batch size + input planes
  int64_t batchSize = input->size[0];

  // Resize temporary columns
  // 重要：gradColumns 现在变成27 x 9的形式, 表示梯度对应的结构. 
  THCTensor_(resize2d)(state, gradColumns, nInputPlane*kW*kH, outputHeight*outputWidth);
  
  ...
  
  // Helpers
  // 没找到THCTensor_(new)对应的内容,
  // 其含义应该是创建了两个新的Tensor, 分别名为gradInput_n和gradOutput_n
  THCTensor *gradInput_n = THCTensor_(new)(state);
  THCTensor *gradOutput_n = THCTensor_(new)(state);

  // For each elt in batch, do:
  for (int elt = 0; elt < batchSize; elt ++) {
    // Matrix mulitply per sample(每个样本都进行矩阵乘法):
    THCTensor_(select)(state, gradInput_n, gradInput, 0, elt);
    // 大胆推测, gradOutput在传入THNN_(SpatialConvolutionMM_updateGradInput)时,
    // 应该是空的.
    THCTensor_(select)(state, gradOutput_n, gradOutput, 0, elt);

    // M,N,K are dims of matrix A and B
    // (see http://docs.nvidia.com/cuda/cublas/#cublas-lt-t-gt-gemm)
    int64_t m = nInputPlane*kW*kH; // 以上面的例子来看, m = 3x3x3 = 27
    int64_t n = gradColumns->size[1]; // 按照THCTensor_(resize2d)(..., gradColumns, ...)来看, n = outputHeight*outputWidth = 3 x 3 = 9
    int64_t k = nOutputPlane; // k = 10

    // Do GEMM (note: this is a bit confusing because gemm assumes column-major matrices)
    // 列优先矩阵, 比如matlab就是列优先(column-major)，也就是说存储一个M*N矩阵，访问顺序为第1列，第2列…第N列。
    // FLOAT——> THCudaBlas_Sgemm
    // HALF ——> THCudaBlas_Hgemm
    // DOUBLE ——> THCudaBlas_Dgemm
    // gradColumns = 1 x op(gradOutput_n) x op(weight)
    #ifdef THC_REAL_IS_FLOAT
    THCudaBlas_Sgemm(
    #elif defined(THC_REAL_IS_HALF)
    THCudaBlas_Hgemm(
    #elif defined(THC_REAL_IS_DOUBLE)
    THCudaBlas_Dgemm(
    #endif
        state,
        'n', 't',
        n, m, k,
        ScalarConvert<int, real>::to(1),
        THCTensor_(data)(state, gradOutput_n), n,
        THCTensor_(data)(state, weight), m,
        ScalarConvert<int, real>::to(0),
        THCTensor_(data)(state, gradColumns), n
    );

    // Unpack columns back into input:
    // col2im 已经在笔记上进行了一点说明, 在PyTorch新版中, caffe2和Aten都有相应的实现
    // caffe2的在caffe2/operators/im2col_op.cc
    // aten的在aten/src/THCUNN/generic/Col2Im.cu(CUDA) & aten/src/THNN/generic/Col2Im.c(C)
    // CUDA版的col2im定义在 pytorch/aten/src/THCUNN/im2col.h 的末尾

    col2im<real, accreal>(
      THCState_getCurrentStream(state),
      THCTensor_(data)(state, gradColumns),
      nInputPlane, inputHeight, inputWidth, outputHeight, outputWidth, kH, kW, padH, padW, dH, dW,
      1, 1, THCTensor_(data)(state, gradInput_n)
    );
  }
...

代码的注释在里面，一些我认为不重要的地方已经忽略，看到这里，大家估计会有很多的问号？这到底啥玩意啊？
下面将对其中涉及到的一些重点进行更细的分析，这里我们需要以用具体的数值为例进行描述，以便于读者更直观的理解。

4. 输入量化（对里面的参数用形象的数值替换，便于理解。）

输入为3通道的RGB图像 channel = nInputPlane = 3
输入图片尺寸Inputsize = 9 x 9
channel = 3
卷积核kW = kH = 3
padW = padH = 0
dW =dH = 3
输出通道为nOutputPlane =10

• Q1： THCTensor_(resize4d)和THCTensor_(resize2d)有啥用？
  Answer：如下图，resize4d把gradInput变成N x C x H x W结构的形式，这里面把batchsize变成1，相当于做了一个unsqueeze的操作。

  THCTensor_(resize4d)(state, gradInput, batchSize, nInputPlane, inputHeight, inputWidth);
  

  resize2d将gradColumns 变成27 x 9的形式.

  THCTensor_(resize2d)(state, gradColumns, nInputPlane*kW*kH, outputHeight*outputWidth);
  

• Q2. Helpers作用？THCTensor *gradInput_n和THCTensor *gradOutput_n的作用？
  Answer：没找到THCTensor_(new)对应的内容, 其含义是创建了两个新的Tensor, 分别名为gradInput_n和gradOutput_n。用于进行后续的操作，即对每个batch，是对其中的每个样本进行逐个串行计算的，也就是gradInput_n是gradInput中的其中1个样本对应的内容，比如gradInput为64 x 32 x 3，第1维表示batchsize，那么gradInput_n就是 1 x 32 x 3，gradOutput_n同理。

// For each elt in batch, do:
 for (int elt = 0; elt < batchSize; elt ++) {
   // Matrix mulitply per sample(每个样本都进行矩阵乘法):
   THCTensor_(select)(state, gradInput_n, gradInput, 0, elt);
   //  gradOutput在传入THNN_(SpatialConvolutionMM_updateGradInput)时, 为空.
   THCTensor_(select)(state, gradOutput_n, gradOutput, 0, elt);
   ...
   }

这部分代码的作用是：将gradInput的第elt个样本提出来，放到gradInput_n中，对gradOutput同理。

• Q3. gradColumns作用？
  Answer： 保存汇总权重梯度中间结果的矩阵，根据Q4中描述的Sgemm等广义矩阵乘积操作定义的，已知权重的值（weight）和权重的梯度（gradOutput_n）容易得知其用处。
  在本例中，被resize为27 x 9的形式, 表示梯度对应的结构。

  THCTensor_(resize2d)(state, gradColumns, nInputPlane*kW*kH, outputHeight*outputWidth);
  

• Q4. GEMM计算
  Answer： GEMM是广义矩阵乘积操作的简称[4]，可以简单理解为将卷积操作变成矩阵乘法，形式如下：
  

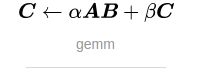
GEMM在深度学习中发挥了十分重要的作用，全连接层以及卷积层基本上都是通过GEMM来实现的，而网络中大约90%的运算都是在这两层中。而一个良好的GEMM的实现可以充分利用系统的多级存储结构和程序执行的局部性来充分加速运算。

其接口如图[4]：

在PyTorch中，接口跟这个类似，不同之处在于加了一个参数（THCState *state）,
容易看出ScalarConvert::to(1)和ScalarConvert::to(0)分别表示sgemm中的
ALPHA和BETA。

其中，ScalarConvert结构体定义在pytorch/aten/src/THC/THCNumerics.cuh中

补充说明，在CUDA编程中，当函数前缀中使用__host__ __device__时，表示对应的函数将会被编译为两个版本，分别可以由CPU和GPU线程调用[6]。

接着回来说GEMM，我们需要知道里面的这些参数的定义才能更好的理解在PyTorch中调用此库的逻辑：

以SGEMM为例（SGEMM的代码是1989年2月8号写的，远古代码…，此外sgemm中的s表示是单精度的运算，类似的，还有dgemm，表示双精度的运算。），它是用于实现矩阵-矩阵运算的广义矩阵运算，根据其参数，计算逻辑是：
$$C:=alpha\ast op(A)\ast op(B)+beta\ast C$$

其中，op(X)可能是op(X) = X, op(X) = X**T(转置)的两种中的一种。
alpha和beta都是标量，A, B, C都是矩阵，其中A为m x k的矩阵，B为 k x n的矩阵， C为 m x n的矩阵。

M表示op(A)和矩阵C的行数（Rows）

N表示op(B)和矩阵C的列数（Columns）

K表示op(A)的列数和op(B)的行数（Rows）

在convNd的函数中，SGEMM/DGEMM等使用的beta = 0， alpha = 1，也就是说：
$$C:=alpha\ast op(A)\ast op(B)$$

下面将其对应到THNN_(SpatialConvolutionMM_updateGradInput)中使用的SGemm：

其所采用的TRANSA = ‘n’， TRANSB = ‘t’。

根据文档[5]定义，当TRANSA = ‘N’ or ‘n’, op( A ) = A. TRANSA = ‘T’ or ‘t’, op( A ) = A**T（A的转置）. TRANSA = ‘C’ or ‘c’, op( A ) = A**T.，所以op(A) = A, op(B) = B**T。

接着，LDA，LDB和LDC都是integer，表示矩阵A、B、C的第一维度的大小。TRANSA = ‘N’ or ‘n’ then
LDA must be at least max( 1, m ), otherwise LDA must be at least max( 1, k ). 对本例中的A，因为TRANSA = ‘n’，所以LDA= max(1, m)，对B，因为TRANSB = ‘t’，所以LDB = max(1, n)。

最后，需要对C进行一下说明：C就是 M X N的矩阵。因为LDC = max(1, m)（没有TRANSC这个东西存在），在exit的时候
C会被 $alpha\ast op(A)\ast op(B)+beta\ast C$的矩阵overwritten。

根据SGEMM中的设置，得知本例中：LDA = n，LDB = m， LDC = n ，对应的
也就是说A = op (A)为n x k，B = op(B)^T为k x m，C为n x m。根据代码定义，有：

m = nInputPlane × kW x kH = 3 x 3 x 3 = 27
n = gradColumns->size[1] 为9
k = 10（nOutputPlane，我这里设的是10。）

A = THCTensor_(data)(state, gradOutput_n)
B = THCTensor_(data)(state, weight)
C = THCTensor_(data)(state, gradColumns)

联想第2.1和2.2节的内容，可以知道这里的gradColumns就是根据当前$l+1$层的误差信号${\delta }^{i,l+1}\odot {\sigma }^{\prime }(z^l)$ = gradOutput_n 和 当前$l+1$层的权重weight = weight求得（根据下式）。

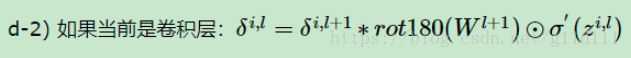
• Q5. col2im计算是什么？
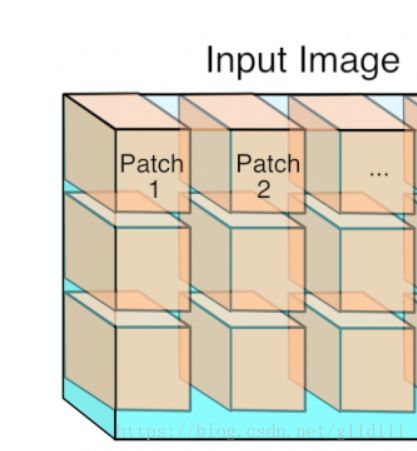
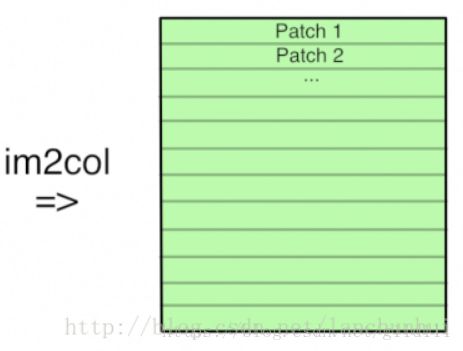
  Answer：col2im在第2.3节[7]稍微提到了一下：

作用是将1xCxHxW的输入图像，根据卷积核的情况拆分为一个个Patch（图中的例子取kW = kH，stride = kW），这样就跟实际的卷积核展开后的维度互为转置，可以容易的用向量乘法进行计算了。

代码如下（这里有个小惊喜，修改了pytorch/aten/src/THCUNN/im2col.h的一个问题，已被merge了，哈哈）

    // Unpack columns back into input:
    // col2im在PyTorch新版中, caffe2和Aten都有相应的实现
    // caffe2的在caffe2/operators/im2col_op.cc
    // aten的在aten/src/THCUNN/generic/Col2Im.cu(CUDA) & aten/src/THNN/generic/Col2Im.c(C)
    // CUDA版的col2im定义在 pytorch/aten/src/THCUNN/im2col.h 的末尾

    col2im<real, accreal>(
      THCState_getCurrentStream(state),
      THCTensor_(data)(state, gradColumns),
      nInputPlane, inputHeight, inputWidth, outputHeight, outputWidth, kH, kW, padH, padW, dH, dW,
      1, 1, THCTensor_(data)(state, gradInput_n)
    );
  }

我们这里看pytorch/aten/src/THCUNN/im2col.h

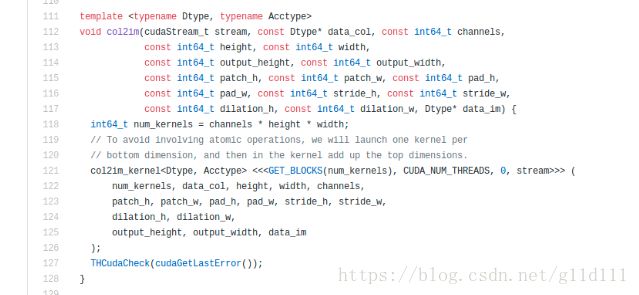
这里先不关注最下面的col2im_kernel的计算逻辑。对比col2im中传入的参数，这里容易发现：
col2im中的data_col就是gradColumns这个指针；
channels就是nInputPlane（比如以分析的例子来讲，一个图片为3通道的RGB图像，那么其nInputPlane就是3，输入的长度和宽度都是9，kW和kH都是3）；
dilation_h, dilation_w取得都是1，如果设为更大的值，效果可见参考资料[8]中的dilation设置大于1的情况的示意图；data_im是gradInput_n。

综上，因为data_col也就是gradColumns其实是保存权重梯度的矩阵。那么data_im就是根据col2im_kernel设计的逻辑来将这些权重梯度进行汇总的操作。

5. 验证
   为了验证自己的思路，我去论坛问了一下，热心的版主alban D回复了我[9]，可以看出，我的分析是没错的哈哈。
   
   

3.2 THNN_(SpatialConvolutionMM_accGradParameters)

1. 方法定义：
   

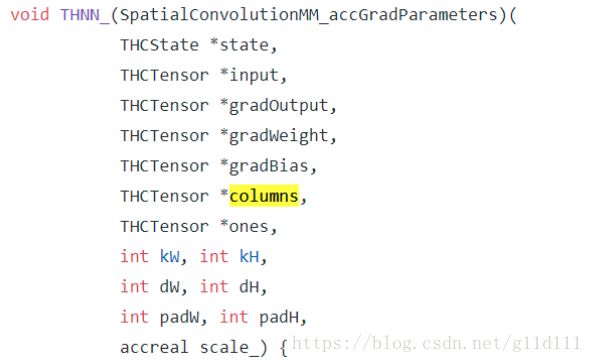
2. 部分参数说明：
   gradOutput是由THNN_(SpatialConvolutionMM_updateGradInput) 计算得到的误差信号${\delta }^l$。
   gradWeight和gradBias根据方法THNN_(SpatialConvolutionMM_accGradParameters)的情况，可以看出它是scale*op(columns)*op(gradOutput_n)（gradOutput_n是从gradOutput（共有batchsize个gradOutput_n）中提取出来的一个个slice。）
   input是由autograd返回的$a^{(l-1)}$，用于在下面的权值更新中发挥作用。
   columns跟方法THNN_(SpatialConvolutionMM_updateGradInput)中的grad_columns作用类似，为了提高效率，缓存weight（权值）的中间结果之用。
   ones 方法THNN_(SpatialConvolutionMM_updateGradInput)中的grad_columns作用也类似，为了提高效率，缓存bias（偏置）的中间结果之用。
   scale_ 这个是权值的学习率，相当于下面中的α
   

3. 总结：
   此方法就不详细展开了，具体结构跟方法THNN_(SpatialConvolutionMM_updateGradInput)类似，其结果是返回gradWeight和gradBias(如果有必要)，然后PyTorch就据此，来更新卷积层的Weight（权重）和Bias（偏置）。

4. 总结

本文仔细的说明了在PyTorch 0.4.1的ATen后端，对于nn.Conv2d的操作进行权重更新的策略进行了详细分析。其中用到的autograd机制，从概念上讲，因为任意维度的张量Back Propagation和向量的Back Propagation完全相同，唯一的区别是如何将数字排列成网格以形成张量。

所以在计算中使用到的GEMM和im2col就是用于将误差信号${\delta }^l$、weight/bias的梯度gradWeight, gradBias的位置进行正确排列用于输出的计算与组合步骤。

在PyTorch后面的章程中，会更新PyTorch Autograd的原理说明，以及此框架跟Symbol 2 Symbol类的框架（Theano和Tensorflow）的区别等内容，欢迎大家提出建议和意见。

最后，Thanks for reading！

参考资料

[1] HIPS/autograd（哈佛HIPS组发布的autograd）
[2] PyTorch Forum——AutoGrad about the Conv2d
[3] 刘建平——《卷积神经网络(CNN)反向传播算法》
[4] NoneLand——《深度学习中GEMM的前世今生》
[5] sgemm官方文档说明
[6] CUDA 函数前缀与存储器前缀讨论
[7] 卷积操作中的矩阵乘法（gemm）—— 为什么矩阵乘法是深度学习的核心所在
[8] CNN概念之上采样，反卷积，Unpooling概念解释
[9] Pytorch Forum——Confused about autograd in Conv2d