R语言 决策树--预测模型
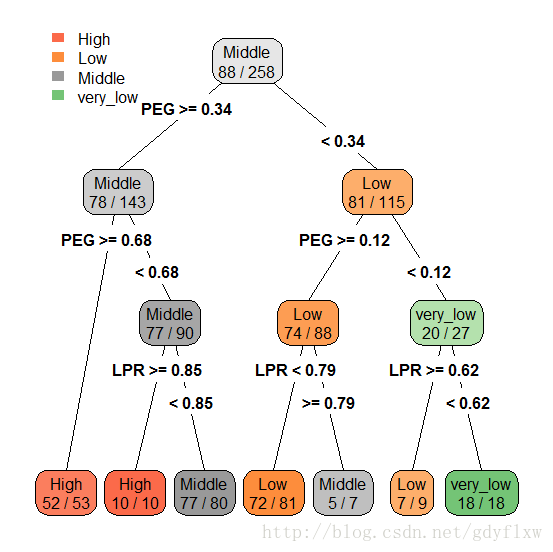
决策树,算法的目标是建立分类预测模型或回归预测模型,是一种预测模型,按目标不同可以细分为分类树和回归树,因为在展示的时候,类似于一棵倒置的树而得名。如下图:
基本概念:
根节点:如上图中最上方,一棵决策树只有一个根节点。
中间节点:位于中间的节点,有上有下的节点。
叶节点:没有后续连续的节点叫叶节点,意味着至此为止。
二叉树和多叉树:每个非节点只有两个分支,叫二叉树,多个就叫多叉树,上图是一个二叉树。
图形怎么看:
如上图,先看根节点,它框内写的是Middle 88/258,意思为在总观测数为258个里面,最大的分类是Middle,有88个,下方两个分支,PEG>=0.34的意思是,左边的分支是PEG>=0.34,右边的分支自然是PEG<0.34(有的图不会显示出来)。从左边的分支看下去,把PEG划分之后,PEG>=0.34的所有观测有143个,其中仍然是Middle分类最多,有78个,然后再按照分支下的分支方法,PEG>=0.34里面,再把它分为>=0.68和<0.68两类,于是在>=0.68这类里面,共有53个,其中最大的是High分类,有52个,这个已经没有必要再分下去了,所以它成为了叶节点。
核心问题
决策树的生长:决策树的本质是分类,就是从根节点开始,一步步区分不同的类别,从而达到最后不能再细分的过程,而这个过程就是生长过程,分支的准确,使差异下降显著,意思即为,假如你有一块奥得奥,一刀切下去,使得切开的两块差异性最大,正确的方法是从夹心层掰开,黑的和黄的两块饼干就分开了,不是么?
决策树的修剪:决策树生长的太过茂盛,这不是好事,它使训练集中每一个数都被分开了,这样就会失去了它的预测意义,这种情况叫过拟合(overfitting)。所以,需要对它进行修剪,把过于精确的部分剪掉,但是,要注意的是,它与错误率是相关的,剪得越多,预测的错误就越高,所以,需要找到合适的剪枝深度。剪枝有预修剪和后修剪两种方式。、
CART分类回归树:
R中建立分类回归树的包是rpart包,还有对应的作图包rpart.plot包两上,使用前先安装,另外,到【User Knowledge Modeling Data Set】这里下载数据集。
library(rpart)
ibbrary(rpart.plot)
#把数据集分为两个部分,训练集TD和测试集PD,分别读入,这里假设已经读入了这两个对象。分别为TD和PD
#自行设置预修剪等相关参数,这里都是默认值,并建立模型
Ctl<-rpart.control(minsplit=2,maxcompete=4,xval=10,maxdepth=10,cp=0.01)
Treefit<-rpart(formula = UNS ~ ., data = TD, method = "class", parms = list(split = "gini"),control=Ctl)
#使用printcp和plotcp查看其复杂参数对模型影响,主要看的是预测误差的标准误xstd,从plotcp里面可以看到与虚线最近的点即为误差最小的点,所以,对应的cp值可以作为修剪的近似值。
printcp(Treefit)
plotcp(Treefit)
#使用prune对树进行修剪,修剪cp值从图中近似得出
prune(Treefit,0.023) #其实这个数据集使用默认参数时就差不多是最优解了,不需要再进行修剪。
#预测训练集和测试集
Pred<-predict(Treefit,TD[,1:5],type="class")
Pred2<-predict(Treefit,PD[,1:5],type="class")
#对比原样本分类
table(Pred,TD[,6])
table(Pred2,PD[,6])
研究表明,分类回归树模型会随训练样本的变化而剧烈变动,所以,需要提高其稳定性,此时,就需要组合预测模型出马。
组合预测模型有两个常见的技术,装袋和推进。原理我也不是很了解,按我个人的理解说一下,如果错误请指正。
装袋:训练集中不放回抽样,得到的数据作为训练数据,未被抽到的作为测试数据,从而建立多个模型并进行预测,预测结果会有误差,而这些误差的大小就作为这些模型的一个权重,当使用整体模型进行预测的时候,其中所有建立的模型均会进行预测,其后由小数服从多数的投票规则选出最终结果。装袋技术对那些数据样本小的波动对模型参数有较大影响的改进效果明显,适用于处理大数据集。
推进:一开始的时候也是不放回随机抽样,但抽完第一次之后,会建立一个模型,以此来预测剩下的数据,如果预测准确,则这一堆数据的权重会上升,反之下降,第二次抽样的时候,就会以权重转化而来的比例去抽样,权重高的被抽到的概率就高。预测的时候,其中所有模型都会进行预测,但不是小数服从多数,而是根据权重来进行投票选择。
这两个技术的R包一个是ipred包中的bagging函数,另一个是adabag包 中的boosting函数,下面是R程序,同样使用上面已经建立好的数据,包需要自行安装
#先是装袋技术
library(ipred)
bt<-bagging(UNS~.,data=TD,coob=T,control=Ctl)
#预测
btp<-predict(bt,PD[,1:5],type="class")
table(btp,PD[,6])
#然后是推进技术
library(adabag)
bst<-boosting(formula = UNS ~ ., data = TD, boos = T, mfinal = 25, coeflearn = "Breiman")
bstp<-predict(bst,PD[,1:5],type="class")
table(bstp,PD[,6])
随机森林
随机森林模型也是基于装袋技术,但它会完全随机建立出N棵树,然后通过对训练集中未被抽中的的数据进行预测,并对这N棵树进行相应的相关分析,把某一方面准确度的树关联在一起,有个形象的解释就是,对某一个变量,这几棵树解释度高,准确率高,是专家,但对另一个变量,则是另外几棵树,相当于专家会诊!
R语言中的包是randomForest包中的randomForest函数
library(randomForest)
rFM<-randomForest(formula = UNS ~ ., data = TD, importance = T)
rFMPP<-predict(rFM,PD[,-6])
table(rFMPP,PD[,6])
#另外可以使用important和varImpPlot两个函数来查看各解释变量对因变量的重要程度。
importance(rFM,type=1)
varImpPlot(rFM,sort=T,n.var=nrow(rFM$importance))
决策树除了这些还有C4.5、C5.0等等,后续有时间再学习,并补充吧。