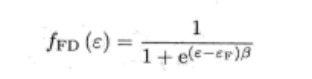神经网络的物理学解释(一)---权重与概率幅
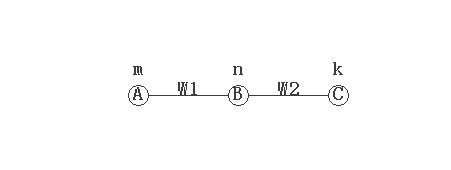
假设在m,n,k位置上有三个球A,B,C
现在让A撞向B,同时也让C撞向B,无论这三个小球是如何相互作用的,不管是强相互作用,弱相互作用,电磁力,或者是引力,也不管作用方向,作用力的大小,总之这两次碰撞的结果都可以用B球在n点出现概率的变化来表示,B球在n点出现的概率w3=w1+w2
制作一个简单1*2*2的神经网络,B点的输入很显然是A*Wab,按照波动力学,概率幅和电子电荷相乘就代表了电荷在空间的实际分布,把A看作电荷,Wab是归一化的权重当然也可以看作是概率幅,A*Wab就是B点的电荷的分布。
然后用Fermi-Dirac分布函数做激活函数
但是把β=1 ,εF=0
β≡1/(kB*T)
KB是玻尔兹曼常数
T是温度
εF系统中电子的化学势
ε是能量,假设能量是与B点电荷的分布有关,并且考虑电性让B点的能量
ε=(-1)*A*Wab
这样就把Fermi-Dirac分布函数变成了sigmoid分布函数
按照Fermi-Dirac的物理意义,S(x)=1/(1+e^(-A*Wab))的意义就是B粒子占据能量-A*Wab的几率。比如S(x)=0.1的意思就是在B位置能量为-A*Wab的粒子数可能为0.1个
同理C点就是C粒子占据能量 -(B*Wbc+D*Wdc)的几率。