动态规划和贪婪算法

1：动态规划

满足如下条件的问题，可以使用动态规划来解决

• 求一个问题的最优解
• 这个问题可以分为若干个子问题
• 子问题又可以被分为更小的子问题

例子

给一根长度为n的绳子，把绳子剪成m段，求m段的最大乘积是多少？

当绳子长度为0的绳子：最大乘积为0
当绳子长度为1绳子：最大乘积为1
当绳子长度为2绳子：最大乘积为2
当绳子长度为3绳子：最大乘积为3
长度为4的绳子可以分为2和2:最大乘积为   2*2 = 4
长度为5的绳子可以分为2和3：最大乘积为   2*3 = 6

:import java.io.IOException;
import java.util.*;


public class Main {
    public static void main(String[] args) throws IOException {
        System.out.println(cutRope(4));
    }

    public static int cutRope(int ropeLen){
    	//由于绳子必须要被划分，所以当绳子长度为0 1 2 3时结果如下
        if (ropeLen < 2)
            return 0;
        if (ropeLen == 2)
            return 1;
        if (ropeLen == 3)
            return 2;

		//数组中的绳子长度由于是划分后的结果，所以不是必须要切割的类型，3可以不切割，最大乘积就为3
        List<Integer> maxs = new LinkedList<>();
        maxs.add(0);
        maxs.add(1);
        maxs.add(2);
        maxs.add(3);
        if (ropeLen < 4){
            return maxs.get(ropeLen);
        }
        for (int i=4; i<=ropeLen; i++){
            int max = 0;
            for (int j=1; j<=ropeLen / 2; j++){
                int content = maxs.get(j) * maxs.get(i - j);
                if (content > max){
                    max = content;
                }
            }
            maxs.add(max);
        }
        return maxs.get(ropeLen);
    }
}

可以证明当绳子长度为3时，乘积最大（证明略），那么我们要划分尽可能多的长度为3的绳子，如果不能划分出长度为3的绳子，就要尽可能划分出长度为2的绳子

2：贪婪算法

import java.io.IOException;
import java.util.*;


public class Main {
    public static void main(String[] args) throws IOException {
        System.out.println(cutRope(4));
    }

    public static int cutRope(int ropeLen) {
        if (ropeLen < 2)
            return 0;
        if (ropeLen == 2)
            return 1;
        if (ropeLen == 3)
            return 2;
        if (ropeLen == 4)
            return 4;

        int count3 = ropeLen / 3;
        int count2 = (ropeLen - count3 * 3) / 2;
        Double max = Math.pow(3, count3) * Math.pow(2, count2);
        return max.intValue();
    }
}

3：LeetCode 198 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你在不触动警报装置的情况下，能够偷窃到的最高金额。

示例 1:

输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
     偷窃到的最高金额 = 1 + 3 = 4 。



示例 2:

输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
     偷窃到的最高金额 = 2 + 9 + 1 = 12 。

通过树形图，将选择展开，蓝色部分代表存在重叠子问题

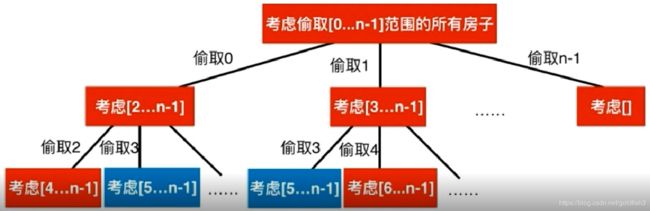
状态的定义，在递归的过程中是不变的
递归 = 状态 + 状态转移

使用记忆化搜索解决

import java.util.*;
class Solution {
    private int[] memo;
    
    //考虑抢劫 [index,nums.length] 中的房子
    private int robCore(int[] nums,int index){
        if (index >= nums.length){
            return 0;
        }
        if (memo[index] != -1){
            return memo[index];
        }
        int res = 0;
        for (int i=index; i<nums.length; i++){
            res = Math.max(res,nums[i] + robCore(nums,i+2));
        }
        memo[index] = res;
        return res;
    }

    public int rob(int[] nums) {
        this.memo = new int[nums.length];
        Arrays.fill(memo,-1);
        return robCore(nums,0);
    }
}

使用动态规划解决

public int rob(int[] nums) {
        if (nums.length <= 0){
            return 0;
        }

        int n = nums.length;
        memo = new int[nums.length];
        memo[n-1] = nums[n-1];

        //[0,n-3]
        for (int i=n-2; i>=0; i--){
            for (int j=i; j<n; j++){
                memo[i] = Math.max(memo[i],nums[j] + (j+2 < n ? memo[j+2] : 0));
            }
        }
        return memo[0];
    }

4：最长上升子序列

csdn又出问题了，插不了图。。。
给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例:

输入: [10,9,2,5,3,7,101,18]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

int lengthOfLIS(vector<int>& nums) {
    //memo[i]表示以i結尾的最长上升子序列的长度
    vector<int> memo(nums.size(),1);

    for (int i = 0; i < nums.size(); ++i) {
        for (int j = 0; j < i; ++j) {
            if (nums[j] < nums[i]){
                memo[i] = max(memo[i],memo[j] + 1);
            }
        }
    }

    int res = 0;
    for (int i = 0; i < memo.size(); ++i) {
        res = max(res,memo[i]);
    }
    return res;
}

5:分割等和子集

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意:

每个数组中的元素不会超过 100
数组的大小不会超过 200

示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

输入: [1, 2, 3, 5]

输出: false

解释: 数组不能分割成两个元素和相等的子集.

使用记忆化搜索

class Solution{
private:
    //-1表示未计算，0表示不可以填充，1表示可以填充
    vector<vector<int>> memo;
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        int n = nums.size();
        for (int i = 0; i < nums.size(); ++i) {
            sum += nums[i];
        }
        if (sum % 2 != 0){
            return false;
        }
        memo = vector<vector<int>>(n,vector<int>(sum/2+1,-1));
        bool res = partitionCore(nums,n-1,sum / 2);
        return res;
    }

    //[0,index]之内可以找到和为sum的子序列
    bool partitionCore(vector<int> & nums,int index,int sum){
        if (sum == 0){
            return true;
        }
        if (sum < 0 || index < 0){
            return false;
        }
        if (memo[index][sum] == -1){
            if (partitionCore(nums,index-1,sum) || partitionCore(nums,index-1,sum-nums[index])){
                memo[index][sum] = 1;
            }else{
                memo[index][sum] = 0;
            }
        }
        return memo[index][sum];
    }
};

使用动态规划

class Solution{
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        int sum = 0;
        for (int i = 0; i < n; ++i) {
            sum += nums[i];
        }
        if (sum % 2 != 0){
            return false;
        }
        int C = sum / 2;
        vector<bool> memo(C+1,false);

        //只是用第一个元素填充
        for (int i = 1; i <= C; ++i) {
            memo[i] = (i == nums[0]);
        }

        for (int i = 1; i < n ; ++i) {
            for (int j = C; j >= nums[i]; --j) {
                memo[j] = memo[j] || memo[j - nums[i]];
            }
        }
        return memo[C];
    }
};