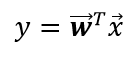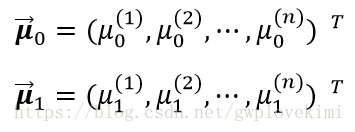机器学习笔记之（4）——Fisher分类器（线性判别分析，LDA）

本博文为Fisher分类器的学习笔记~

本博文主要参考书籍为：

• 《Python大战机器学习》

Fisher分类器也叫Fisher线性判别（Fisher Linear Discriminant），或称为线性判别分析（Linear Discriminant Analysis，LDA）。LDA有时也被称为Fisher's LDA。最初于1936年，提出Fisher线性判别，后来于1948年，进行改进成如今所说的LDA。

线性模型

对于给定样本，其中为样本的第n种特征。线性模型的形式为：

其中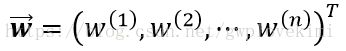，为每个特征对应的权重生成的权重向量。其实这个线性模型也就类似于学习笔记（3）中的sigmoid函数的输入。当然啦，逻辑斯蒂回归也是线性模型之一。

线性模型的物理表示：二维空间就是一条直线，三维空间就是一个平面，推广到n维空间~

常见的线性模型有：岭回归、lasso回归、逻辑斯蒂回归以及Fisher等。正如在上一节笔记中所言，逻辑斯蒂回归分类器构建的过程正是通过训练数据来获得一系列的权重向量。在此处则是拓展为：根据训练数据集来计算参数和。

对于具有N个训练样本的样本集，每个给定的样本（注意，这里是N个训练样本，每个训练样本有n个特征。而样本集中，训练样本的标签为，而预测值为：

则模型的损失函数为：

通过使损失函数最小化，即可以获得要求的参数和；通过梯度下降或者梯度上升算法（最优化算法）可以求解。

关于特征归一化的意义：

特征归一化有两个意义，1、提升模型的收敛速度；2、提升模型的精度。详细分析见下面图片：

LDA或Fisher：

Fisher的基本思想是：

训练时，将训练样本投影到某条直线上，这条直线可以使得同类型的样本的投影点尽可能接近，而异类型的样本的投影点尽可能远离。要学习的就是这样的一条直线。

预测时，将待预测数据投影到上面学习到的直线上，根据投影点的位置来判断所属于的类别。

下面直接给出书上关于LDA的推导过程的照片：

下面结合本人的理解，对推导过程做简单的分析：

将样本投影到直线上，假设直线为

对于标签为0类和1类样本，其特征值的均值为向量（每个样本有多个特征值，每种特征值的均值组成一个向量）：

对应的样例之间的协方差矩阵为和。那么两类样本的中心在直线上的投影分别为和，而两类样本的投影的方差分别为：和。

由于Fisher的准则是：同类型的投影点尽可能近，也即是，两类样本的投影方差都尽可能小，那么他们之和也尽可能小，即尽可能小。而异类型的投影点尽可能远，也就是异类型投影点的中心尽可能远，也就是尽可能的大。那么就可以获得目标函数为：

通过使这个目标函数尽可能的大，就可以满足Fisher判别准则。通过朗格朗日乘子法则可以解决这一最优化的问题。至于其具体的推导过程以及上面书本中的类内离散度矩阵和类间离散度矩阵这些就不一一展开了~个人感觉上面文字描述这部分理解了，Fisher就算大概明白了。scikit-learn中也有LDA的函数，下面给出测试代码~

给出Python代码如下：

from sklearn import datasets, cross_validation,discriminant_analysis

###############################################################################
#用莺尾花数据集
def load_data():
    iris=datasets.load_iris()
    return cross_validation.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0,stratify=iris.target)  
    #返回为: 一个元组，依次为：训练样本集、测试样本集、训练样本的标记、测试样本的标记 
    
###############################################################################
def test_LinearDiscriminantAnalysis(*data):
    x_train,x_test,y_train,y_test=data
    lda=discriminant_analysis.LinearDiscriminantAnalysis()
    lda.fit(x_train,y_train)
    print('Coefficients:%s, intercept %s'%(lda.coef_,lda.intercept_))#输出权重向量和b
    print('Score: %.2f' % lda.score(x_test, y_test))#测试集
    print('Score: %.2f' % lda.score(x_train, y_train))#训练集

###############################################################################
x_train,x_test,y_train,y_test=load_data()
test_LinearDiscriminantAnalysis(x_train,x_test,y_train,y_test)

结果如下图所示：

在测试集上预测准确率为100%，而在训练集上预测准确率为97%。

Fisher的这种映射关系还有一种作用就是作为降维技术，称为监督降维技术（因为是有训练数据的，所以称为监督）

下面来看看原始的数据集经过Fisher投影后的数据集的情况。

from sklearn import datasets, cross_validation,discriminant_analysis

###############################################################################
#用莺尾花数据集
def load_data():
    iris=datasets.load_iris()
    return cross_validation.train_test_split(iris.data,iris.target,test_size=0.25,random_state=0,stratify=iris.target)  
    #返回为: 一个元组，依次为：训练样本集、测试样本集、训练样本的标记、测试样本的标记 
    

###############################################################################
def plot_LDA(converted_X,y):
    '''
    绘制经过 LDA 转换后的数据

    :param converted_X: 经过 LDA转换后的样本集
    :param y: 样本集的标记
    :return:  None
    '''
    from mpl_toolkits.mplot3d import Axes3D
    import matplotlib.pyplot as plt 
    fig=plt.figure()
    ax=Axes3D(fig)
    colors='rgb'
    markers='o*s'
    for target,color,marker in zip([0,1,2],colors,markers):
        pos=(y==target).ravel()
        X=converted_X[pos,:]
        ax.scatter(X[:,0], X[:,1], X[:,2],color=color,marker=marker,
			label="Label %d"%target)
    ax.legend(loc="best")
    fig.suptitle("Iris After LDA")
    plt.show()
    

###############################################################################
import numpy as np
x_train,x_test,y_train,y_test=load_data()
X=np.vstack((x_train,x_test))#沿着竖直方向将矩阵堆叠起来，把训练与测试的数据放一起来看
Y=np.vstack((y_train.reshape(y_train.size,1),y_test.reshape(y_test.size,1)))#沿着竖直方向将矩阵堆叠起来
lda = discriminant_analysis.LinearDiscriminantAnalysis()
lda.fit(X, Y)
converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_
plot_LDA(converted_X,Y)

结果如下图所示：

可以看出，Fisher确实能够实现降维。假设存在M个类，则多分类LDA可以将样本投影到M-1维空间。

好~关于Fisher分类器的学习笔记告一段落，后续有新的体会会及时更新，欢迎广大读者朋友赐教

补充：

通过线性判别分析压缩无监督数据

LDA是一种可作为特征抽取的技术，它可以提高数据分析过程中的计算效率，同时，对于不适用于正则化的模型，它可以降低因维度灾难带来的过拟合。

LDA的基本概念与PCA非常相似（见博文机器学习笔记6）。PCA试图在数据集中找到方差最大的正交的主成分分量的轴，而LDA的目标是发现可以最优化分类的特征子空间。其中，PCA是无监督算法，而LDA是监督算法，因此，直观上，LDA比PCA更优越。如下图所示：

如图所示，在x轴方向（LD1），通过线性判定，可以很好地将呈正态分布的两个类分开。虽然沿y轴（LD2）方向的线性判定保持了数据集较大方差，但是沿此方向无法提供关于类别区分的任何信息，因此它不是一个好的线性判定。一个关于LDA的假设是：数据呈正态分布。此外，还假设各类别中数据具有相同的协方差矩阵，且样本的特征从统计上来讲是相互独立的。不过即使一个或多个假设没有满足，LDA仍旧可以很好的完成降维工作。

给出LDA数据降维和逻辑斯蒂回归分类的Python代码如下：

#####################################定义一个画图函数###########################
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap

def plot_decision_regions(X, y, classifier, resolution=0.02):

    # setup marker generator and color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # plot the decision surface
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
                           np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())

    # plot class samples
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], 
                    y=X[y == cl, 1],
                    alpha=0.6, 
                    c=cmap(idx),
                    edgecolor='black',
                    marker=markers[idx], 
                    label=cl)


##############################数据的读入、划分、标准化###########################
import pandas as pd
#Python Data Analysis Library 或 pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。
#Pandas 纳入了大量库和一些标准的数据模型，提供了高效地操作大型数据集所需的工具。
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
#读入csv文件，形成一个数据框
#使用葡萄酒数据集


from sklearn.cross_validation import train_test_split
x, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
x_train, x_test, y_train, y_test =train_test_split(x, y, test_size=0.3,stratify=y,random_state=0)
#葡萄酒数据集划分为训练集和测试集，分别占据数据集的70%和30%

#使用单位方差对数据集进行标准化
from sklearn.preprocessing import StandardScaler
sc=StandardScaler()
#注意，当改为from sklearn.preprocessing import StandardScaler as sc时，会报错
# fit_transform() missing 1 required positional argument: 'X'。这就是由于sc没有StandardScaler()而仅仅是StandardScaler
x_train_std=sc.fit_transform(x_train)
x_test_std=sc.fit_transform(x_test)


#####################################使用sklearn中的LDA类#######################
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)#选取两个主成分
#做降维处理
x_train_lda = lda.fit_transform(x_train_std, y_train)
x_test_lda=lda.transform(x_test_std)

#用逻辑斯蒂回归进行分类(对训练数据进行处理)
lr=LogisticRegression()
lr.fit(x_train_lda,y_train)
plot_decision_regions(x_train_lda,y_train,classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

#用逻辑斯蒂回归进行分类(对测试数据进行处理)
lr=LogisticRegression()
lr.fit(x_train_lda,y_train)
plot_decision_regions(x_test_lda,y_test,classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()

结果如图所示：

可与机器学习笔记（6）中的PCA做一下对比~

此部分主要参考书籍为：

• 《Python机器学习》