数据平滑方法的原理和应用

一、简介

在实际的工程应用中，经常会遇到初始结果噪声太多的问题，比如信号强度抖动的太厉害，比如视频流中的bbox抖动的太厉害，比如光谱信号抖动的太厉害等等，这时候就需要一些简单的滑动平均算法。滑动平均其实是一个很朴素的方法，但是要与实际结合，构造出合适的平滑方式，是需要一些思考的。下面我将分别介绍滑动平均法（Mean Average）、指数滑动平均法（Exponential Mean Average）、SG滤波法（Savitzky Golay Filter）。

二、滑动平均法

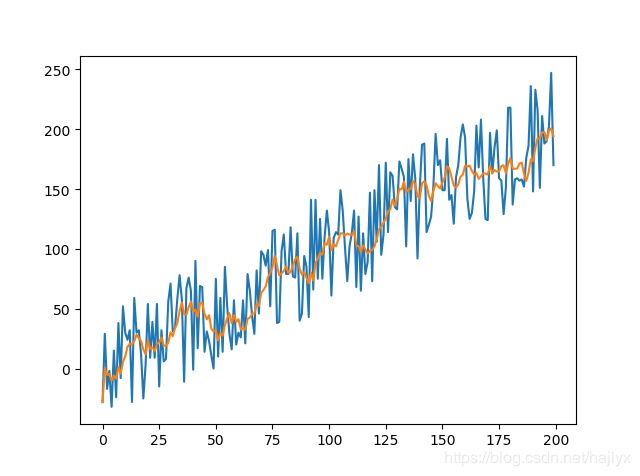
简单来说，滑动平均法把前后时刻的一共2n+1个观测值做平均，得到当前时刻的滤波结果。这是一个比较符合直觉的平滑方法，在生活中、工作中很经常会用到，但是很少去思考这么做的依据是什么，下面我就来仔细分析一下其中的原理。
对于一个观测序列，我们有这样的假设：每一次的观测值是带有噪声的，而我们期望噪声的均值为0，方差为${\sigma }^2$，观测值和真实值之间的关系如下：
$$g_t=x_t+{\epsilon }_t(1)$$其中，$x_t$为观测值，$g_t$为真实值，${\epsilon }_t$为噪声。为了降低噪声的影响，我们把相邻时刻的观测值相加后平均，公式如下：
$$p_t=\frac{{\sum }_{i=1}^n(x_{t-i}+x_{t+i})+x_t}{2n+1}(2)$$ $p_t$表示 t 时刻的滤波结果，$x_{t-1}$表示 t-1 时刻的观测值， n 代表滑动窗口半径。将公式（1）代入公式（2），可以得到
$$p_t=\frac{{\sum }_{i=1}^n(g_{t-i}+g_{t+i})+g_t-{\sum }_{i=1}^n({\epsilon }_{t-i}+{\epsilon }_{t+i})-{\epsilon }_t}{2n+1}(3)$$前面说到了，我们假设噪声的均值为0，所以${\sum }_{i=1}^n({\epsilon }_{t-i}+{\epsilon }_{t+i})+{\epsilon }_t$为0，那么我们得到的结果就是:
$$p_t=\frac{{\sum }_{i=1}^n(g_{t-i}+g_{t+i})+g_t}{2n+1}(4)$$当观测数据的真实值变化较小时，或者变化为线性时，可以近似认为：
$$p_t=\frac{{\sum }_{i=1}^n(g_{t-i}+g_{t+i})+g_t}{2n+1}=g_t(5)$$从上面的分析过程我们可以看到，当滑动窗口内的真实数据变化不大的时候，我们可以抑制掉很大一部分噪声，滤波结果近似真实值；当滑动窗口内的真实值变化较大时，这种滤波方式就会损失一部分精确度，滤波结果接近真实值的平均期望。所以，窗口的大小会对滤波结果有很大影响。窗口越大，滤波结果越平滑，但会一定程度上偏离真实值；窗口越小，滤波结果越接近观测值，但噪声偏大。

滑动平均法还有一个升级版本，也就是加权滑动平均法。实际场景中，每个观测值的重要程度不同，忽略每个观测值的置信度直接平均不能得到精确的结果，所以就需要给观测值加权。加权滑动平均法的公式如下：
$$p_t=\frac{{\sum }_{i=1}^n(x_{t-i}\ast w_{t-i}+x_{t+i}\ast w_{t+i})+x_t\ast w_t}{2n+1}(6)$$ $w_t$为 t 时刻的权重。（6）式表示的是把每个观测值乘以权重后再平均。这种方法适用于观测值本身带有置信度的情况。注意，这里有一个小问题，如果置信度的取值范围是0到1之间，那么加权之后计算得到的观测值往往小于真实值，我来解释一下为什么。首先，我们假设观测值和真实值的均值是相等的，也就是
$$\bar{X}=\frac{{\sum }_{i=1}^{2n+1}{x}_t}{2n+1}=\frac{{\sum }_{i=1}^{2n+1}{g}_t}{2n+1}=\bar{G}(7)$$当我们把观测值乘以权重了之后，观测值和真实值的均值就不相等了，因为真实值的权重均值为1，而观测值的权重均值为$\overline{w_t}={\sum }_{i=1}^n\frac{(w_{t-i}+w_{t+i})+w_t}{2n+1}$，是小于等于1的，最终的预测值也是小于等于真实值的，而且大概率是小于。所以我们需要对（6）式增加一个修正：
$$\widetilde{p_t}=\frac{p_t}{\overline{w_t}}(8)$$这样，得到的预测值就会更加合理了。

小结：滑动平均法使用的前提是，噪声的均值为0，真实值变化不大或线性变化的场景。如果真实值有较高频率的非线性突变的话，滑动平均法的效果就不够好了。同时，滑动平均法的窗口选取很重要，需要根据具体数据来选择。如果需要使用在线版本的滑动平均，那么就要把窗口前移，也就是把当前时刻的前n个观测值进行平均，但这样得到的结果会明显滞后于当前观测值，窗口越大，滞后的现象越严重。

class MovAvg(object):
    def __init__(self, window_size=7):
        self.window_size = window_size
        self.data_queue = []

    def update(self, data):
        if len(self.data_queue) == self.window_size:
            del self.data_queue[0]
        self.data_queue.append(data)
        return sum(self.data_queue)/len(self.data_queue)

三、指数滑动平均法

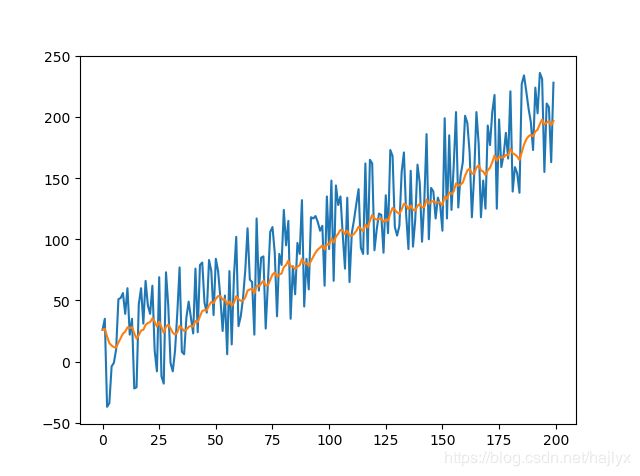
指数滑动平均法相当于加权滑动平均法的变体，主要区别在于，指数滑动平均法的权重是固定的、随时间推移呈指数衰减。指数滑动平均法的公式如下：
$$p_t=w\ast x_t+(1-w)\ast p_{t-1}(9)$$ $p_t$表示预测值， $w$表示衰减权重，通常我们设为固定值0.9， $x_t$表示观测值，这是一个递推公式。前面说了，指数滑动平均法的权重是随时间推移呈指数衰减的，那么上面的这个递推公式的指数体现在哪里呢？我们把（9）式进行延伸：
$$p_{t-1}=w\ast x_{t-1}+(1-w)\ast p_{t-2}(10)$$将（9）和（10）两式子联立，可得
$$p_t=w\ast x_t+(1-w)\ast (w\ast x_{t-1}+(1-w)\ast p_{t-2})(11)$$发现没有，在（11）式中$p_t$与$p_{t-2}$的关系是$(1-w{)}^2$倍，而在（9）式中$p_t$与$p_{t-1}$的关系是$1-w$倍，呈指数衰减关系。同时，在初始时刻有如下关系：
$$p_0=x_0(12)$$根据这一关系和上述的递推公式，我们就能够得到整个算法的公式了。

由于这种指数衰减的特性，指数滑动平均法会比滑动平均法的实时性更强，更加接近当前时刻的观测值。在实际场景下，如果目标的波动较大时，指数滑动平均法会比滑动平均更加接近当前的真实值。那么是不是就说明，指数滑动平均法在任意场景下都比滑动平均法更好呢？不一定。我们来分析一下指数衰减法的误差项，这里为了简便表示，设定 t=2 ，同时，将（1）式和（12）式代入公式（11），可得到误差项：
$$\epsilon =w\ast {\epsilon }_2+(1-w)\ast (w\ast {\epsilon }_1+(1-w)\ast {\epsilon }_0)(13)$$所以误差项也是呈指数衰减的，越接近当前时刻的误差项权重越大。假如在当前的工程场景中，误差是固定的分布，不受目标的观测值大小影响的话，那么指数滑动平均法会更接近真实值；假如误差会受目标观测值影响，比如我们观测的是一个连续运动的目标，中间突然出现了一个偏离很远的观测点，那么这个点为误检的概率相当大，也就是该观测值的误差比之前其他点的误差要大得多，此时指数加权平均法的结果就会波动较大，结果就不如滑动平均了。

小结：当误差不受观测值大小影响的话，指数滑动平均比滑动平均好；当误差随观测值大小变化时，滑动平均比指数滑动平均更好。

class ExpMovAvg(object):
    def __init__(self, decay=0.9):
        self.shadow = 0
        self.decay = decay
        self.first_time = True

    def update(self, data):
        if self.first_time:
            self.shadow = data
            self.first_time = False
            return data
        else:
            self.shadow = self.decay*self.shadow+(1-self.decay)*data
            return self.shadow

四、SG滤波法

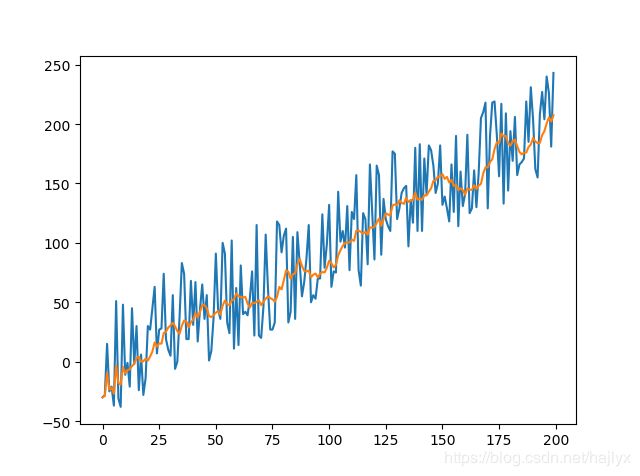
SG滤波法（Savitzky Golay Filter）的核心思想也是对窗口内的数据进行加权滤波，但是它的加权权重是对给定的高阶多项式进行最小二乘拟合得到。它的优点在于，在滤波平滑的同时，能够更有效地保留信号的变化信息，下面我来介绍一下其原理。
我们同样对当前时刻的前后一共2n+1个观测值进行滤波，用k-1阶多项式对其进行拟合。对于当前时刻的观测值，我们用下面的公式进行拟合：
$$x_t=a_0+a_1\ast t+a_2\ast t^2+...+a_{k-1}\ast t^{k-1}(14)$$同样，对于前后时刻（如t-1、t+1、t-2、t+2等时刻）的预测值，我们同样可以用（14）式来计算，这样一共得到2n+1个式子，构成一个矩阵（似乎发不了矩阵，我放个图片吧）：

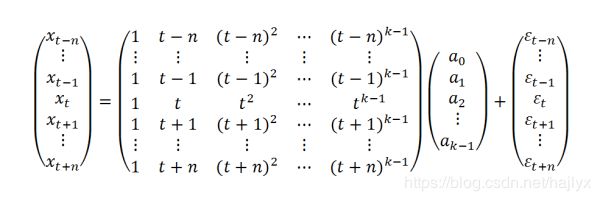
要使得整个矩阵有解，必须满足 2n+1>k，这样我们才能够通过最小二乘法确定参数$a_0$、$a_1$、$a_2$、…$a_{k-1}$。我们把上面的矩阵简化表示为下面公式：
$$X_{(2n+1)\times 1}=T_{(2n+1)\times k}+A_{k\times 1}+E_{(2n+1)\times 1}(15)$$各个参数下标表示它们各自的维度，如$A_{k\times 1}$表示有k行1列的参数。通过最小二乘法，我们可以求得$A_{k\times 1}$的解为：
$$A=(T^{trans}\cdot T{)}^{-1}\cdot T^{trans}\cdot X(16)$$上标$trans$表示转置。那么，模型的滤波值为：
$$P=T\cdot A=T\cdot (T^{trans}\cdot T{)}^{-1}\cdot T^{trans}\cdot X=B\cdot X(17)$$ 最终可以得到滤波值和观测值之间的关系矩阵：
$$B=T\cdot (T^{trans}\cdot T{)}^{-1}\cdot T^{trans}(18)$$ 算出了B矩阵，我们就能够快速的将观测值转换为滤波值了。
小结：SG滤波法对于数据的观测信息保持的更好，在一些注重数据变化的场合会比较适用。

class SavGol(object):
    def __init__(self, window_size=11, rank=2):
        assert window_size % 2 == 1
        self.window_size = window_size
        self.rank = rank

        self.size = int((self.window_size - 1) / 2)
        self.mm = self.create_matrix(self.size)
        self.data_seq = []

    def create_matrix(self, size):
        line_seq = np.linspace(-size, size, 2*size+1)
        rank_seqs = [line_seq**j for j in range(self.rank)]
        rank_seqs = np.mat(rank_seqs)
        kernel = (rank_seqs.T * (rank_seqs * rank_seqs.T).I) * rank_seqs
        mm = kernel[self.size].T
        return mm

    def update(self, data):
        self.data_seq.append(data)
        if len(self.data_seq) > self.window_size:
            del self.data_seq[0]
        padded_data = self.data_seq.copy()
        if len(padded_data) < self.window_size:
            left = int((self.window_size-len(padded_data))/2)
            right = self.window_size-len(padded_data)-left
            for i in range(left):
                padded_data.insert(0, padded_data[0])
            for i in range(right):
                padded_data.insert(
                    len(padded_data), padded_data[len(padded_data)-1])
        return (np.mat(padded_data)*self.mm).item()

附录

本文图片制作的相关代码。

import cv2
import numpy as np
import matplotlib.pyplot as plt

import imageio

# 一维数据滤波
ma, ema, sg = MovAvg(), ExpMovAvg(), SavGol()
data_list, data_ma, data_ema, data_sg = [], [], [], []
for i in range(200):
    data = i+np.random.randint(-50, 50)
    data_list.append(data)
    data_ma.append(ma.update(data))
    data_ema.append(ema.update(data))
    data_sg.append(sg.update(data))
plt.plot(data_list, label='raw')
plt.plot(data_ma, label='ma')
plt.plot(data_ema, label='ema')
plt.plot(data_sg, label='sg')
plt.legend()
plt.show()

# 鼠标轨迹滤波
ma_x, ma_y = MovAvg(), MovAvg()
ema_x, ema_y = ExpMovAvg(), ExpMovAvg()
sg_x, sg_y = SavGol(), SavGol()


def draw_circle(event, x, y, flags, param):
    if event == cv2.EVENT_MOUSEMOVE:
        sx = np.random.randint(-50, 51)
        sy = np.random.randint(-50, 51)
        cv2.circle(show, (x+sx, y+sy), 5, (255, 255, 255), -1)
        x, y = ma_x.update(x+sx), ma_y.update(y+sy)
        cv2.circle(show, (int(x), int(y)), 5, (0, 0, 255), -1)
        x, y = ema_x.update(x+sx), ema_y.update(y+sy)
        cv2.circle(show, (int(x), int(y)), 5, (0, 255, 0), -1)
        x, y = sg_x.update(x+sx), sg_y.update(y+sy)
        cv2.circle(show, (int(x), int(y)), 5, (255, 0, 0), -1)


show = np.zeros((1024, 1024, 3), np.uint8)
cv2.namedWindow('image')
buff = []
while True:
    cv2.setMouseCallback('image', draw_circle)
    cv2.imshow('image', show)
    save = cv2.resize(show, (512, 512))
    save = cv2.cvtColor(save, cv2.COLOR_BGR2RGB)
    buff.append(save)
    if cv2.waitKey(100) == ord('q'):
        break
cv2.destroyAllWindows()
imageio.mimwrite('test.gif', buff, 'GIF', duration=0.1)