线性回归－scikit-learn

线性回归即是我们希望能通过学习来得到一个各属性线性组合的函数，函数的各项系数表明了该属性对于最后结果的重要性，可以用以下公式表达：

yˆ(ω,x)=ω1x1+ω2x2+...+ωpxp+b

普通最小二乘法

线性回归试图让各个点到回归直线上的距离和最小，即最小化均方误差。可用以下公式描述

minω∥Xω−y∥22

通过一个例子简单学习一下scikit-learn的线性回归

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model

导入数据并查看

# 从datasets导入数据
diabetes = datasets.load_diabetes()
diabetes.data.shape

(442, 10)

# 我们只去其中第三列数据使用
diabetes_X = diabetes.data[:, np.newaxis, 2]
diabetes_X.shape

(442, 1)

# 查看前十个数据
diabetes_X[:10]

array([[ 0.06169621],
       [-0.05147406],
       [ 0.04445121],
       [-0.01159501],
       [-0.03638469],
       [-0.04069594],
       [-0.04716281],
       [-0.00189471],
       [ 0.06169621],
       [ 0.03906215]])

# 将数据简单分为训练集和测试集,训练集４２２个数据，测试集２０个数据
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# 将目标集合分为训练集和测试集
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

创建一个线性回归模型实例

regr = linear_model.LinearRegression()

通过训练集来训练模型

regr.fit(diabetes_X_train, diabetes_y_train)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

查看回归系数

print('Coefficients:\t', regr.coef_)
print('Intercept:\t',regr.intercept_)

Coefficients:    [ 938.23786125]
Intercept:   152.918861826

也就是说，回归之后得到的直线模型是 y=938.24x+152.92

统计学上把数据点与它在回归直线上相应位置的差异称为残差，把每个残差平方之后加起来 称为残差平方和，它表示随机误差的效应，下面来查看一下残差平方和。

rss = np.mean((regr.predict(diabetes_X_test) - diabetes_y_test)**2)
print('RSS value:\t%.2f' %rss)

RSS value:  2548.07

查看 R2 值

print("Variance score: %.2f" % regr.score(diabetes_X_test, diabetes_y_test))

Variance score: 0.47

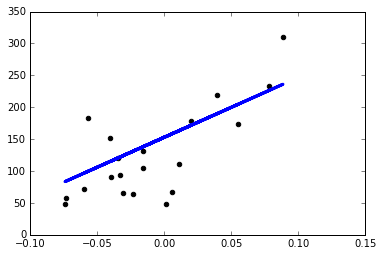
绘制回归图

plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, regr.predict(diabetes_X_test),color='blue',linewidth=3)