【神经网络和深度学习-开发案例】 第二章 神经网络结构

【神经网络和深度学习】

第二章 神经网络结构

---

案例：使用神经网络识别手写数字

我将介绍一个神经网络，它可以很好地对手写的数字进行分类。为了准备这一点，它有助于解释一些术语，让我们可以命名一个网络的不同部分。假设我们有网络：

如前所述，这个网络中最左边的层称为输入层，层中的神经元被称为输入神经元。最右边或输出层包含输出神经元，或者，就像在本例中一样，是一个输出神经元。中间层被称为隐藏层，因为这一层的神经元既不是输入，也不是输出。“隐藏”这个词听起来有点神秘——我第一次听到这个词的时候，我认为它一定有一些深刻的哲学或数学意义——但它的意思只不过是“不是输入或输出”。上面的网络只有一个隐藏的层，但是一些网络有多个隐藏层。例如，下面的四层网络有两个隐藏层：

这种多层网络又被称为多层感知器或MLPs，它们是由S型神经元组成的，而不是感知器。

在网络中输入和输出层的设计通常是直接的。例如，假设我们试图确定一个手写的图像是否描述了一个“9”。设计网络的一种自然方法是将图像像素的强度编码到输入神经元中。如果图像是64×64分辨率的图像，那么我们就有4,096=64× 64输入神经元，在0和1之间适当地缩放。输出层只包含一个神经元，输出值小于0.50.5，表示“输入图像不是9”，值大于0.50.5，表示“输入图像是9”。

虽然神经网络的输入和输出层的设计通常是直接的，但隐藏层的设计却有相当的复杂。特别地，用一些简单的经验法则来总结隐藏层的设计过程是不可能的。相反，神经网络研究人员已经开发出了许多隐藏层的设计方法，帮助人们从他们的网中获得他们想要的行为。例如，这样的启发式可以用来帮助确定如何在培训网络所需的时间内权衡隐藏层的数量。在这本书中，我们将会遇到一些这样的设计启发法。

到目前为止，我们一直在讨论神经网络，其中一个层的输出被用作下一层的输入。这种网络被称为前馈神经网络。这意味着网络中没有循环——信息总是被灌输的，从来没有反馈过。如果我们有循环，我们就会得到函数的输入取决于输出的情况。这是很难理解的，所以我们不允许这样的循环。

前馈神经网络：Feed forward neural networks (FF or FFNN) and perceptrons(P)

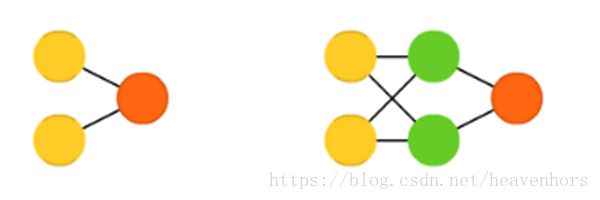
然而，还有其他的人工神经网络模型，在这些模型中，反馈回路是可能的。这些模型被称为周期性神经网络。在这些模型中，我们的想法是让神经元在一定的时间内燃烧，然后变得静止。这种放电可以刺激其他神经元，这可能会在一段时间后发生，也会持续很短的时间。这导致更多的神经元被激活，所以随着时间的推移，我们会产生一连串的神经元放电。循环不会在这样的模型中引起问题，因为神经元的输出只会在以后的某个时间影响它的输入，而不是瞬间。

周期性神经网络：Recurrent neural networks(RNN)

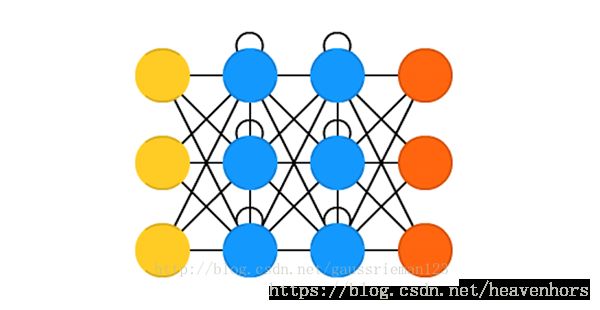
霍普菲尔网络的每个神经元都与其他神经元相连接；它是一碗完全纠缠在一起的意大利面。每个节点在训练前都是输入点，然后训练中都是隐藏节点，训练结束后又是输出节点。这些网络会设定神经元的值为所需要的模式，然后计算全职，通过这种方法来训练模型。在这之后权重不会再改变。一旦训练成一种或多种模式，网络会一直收敛到一种学习好的模式，因为网络只有在这些状态下才是稳定的。注意到它不会一直符合所要的状态。它能够部分稳定是因为全局的“能量”或“温度”在训练中是逐步减少的。

霍普菲尔网络： Hopfield network(HN)

卷积神经网络和大多数其他类型的网络都很不相同。他们最初用来做图像处理，后来也用在其他类型的输入数据比如音频。一个典型的CNN应用是，当你给网络输入图像，网络会对数据进行分类，例如如果你输入的是猫的照片，它会给出标签“猫”。CNN通常以一个输入“扫描仪”开始，而它并不会在理科解析所有的训练数据。举例来说，输入一个200*200像素的图像，你肯定不想要有40000节点的一层。相反，你建立一个扫描输入层比如20*20，把大图像左上角的20*20像素进行扫描。一旦前20*20经过处理，逐像素向右移动这个扫描器来扫描所有的剩余图像。注意到，我们并没有把处理过的20*20像素挪开，也没有把图像分成20*20的小块，而是使用这个20*20的扫描器对所有像素进行扫描。输入数据然后进行卷积层而不是普通曾，意味着不是所有的节点都和其他节点相连接。每个节点都只和她最近的节点相连（远近取决于具体的实现，但通常不会很多）。这些卷积层也倾向于变小当它们越老越深的时候，通常是输入大小最容易整除的因子（如20可能变成10，然后5）。2的幂在这里会经常被使用，因为它们能够很完全的分离：32,16,8,4,2,1。除了这些卷积层，通常还有特征池化层。池化是一种滤出细节部分的方法：最常用的池化技术是极大值池化，比如我们对2*2的像素，返回其R值最大的像素。对音频使用CNN，我们只需要输入音频波，然后一点一点增加长度。实际中对CNN的使用通常在末端增加一个FFNN用来深入处理数据，通常要能处理高度非线性抽象分类问题。CNN+FFNN这种网络通常称为DCNN，但是DCNN和CNN的名称和缩写通常可以互相代替。

卷积神经网络：Convolutional neural networks (CNN or DCNN)

我们将集中讨论更广泛使用的前馈网络。

一个简单的网络，用来对手写数字进行分类

---

在定义了神经网络之后，让我们回到手写识别。我们可以把识别手写数字的问题分成两个子问题。首先，我们想要一种方法，将包含许多数字的图像分解成一系列单独的图像，每个图像都包含一个数字。举个例子，我们修改以下一张图片

到6个单独的图片

我们人类很容易就能解决这个分割问题，但是对于一个计算机程序来说，正确地分解图像是很有挑战性的。一旦图像被分割，程序就需要对每个数字进行分类。
举个例子，我们希望我们的程序能识别出上面的第一个数字

我们将专注于编写一个程序来解决第二个问题，即对单个数字进行分类。我们这样做是因为一旦你有了一个很好的分类数字的方法，就会发现分割问题并不是那么难解决。有许多方法可以解决分割问题。一种方法是尝试许多不同的分割图像的方法，使用单个数字分类器来对每个试验分割进行评分。如果单个数字分类器对其在所有段中的分类有信心，那么试片的分数就会很高，如果分类器在一个或多个段中有很多麻烦，则会得到较低的分数。这个想法是，如果分类器在某个地方遇到麻烦，那么它很可能会遇到麻烦，因为分割被错误地选择了。这个想法和其他的变化可以很好地解决分割问题。因此，与其担心市场细分，我们将专注于开发一个神经网络，它可以解决更有趣和更困难的问题，即识别单个手写的数字。
为了识别单个数字，我们将使用一个三层神经网络：

网络的输入层包含了编码输入像素值的神经元。
我们的网络训练数据将包括28像素的扫描手写数字，因此输入层包含784=28×28 neurons个神经元。为了简单起见，我省略了上面图表中的大部分784的输入神经元。输入像素是灰度级的，其值为0.0代表白色，值为1.0表示黑色，在表示逐渐变暗的灰色阴影之间。

网络的第二层是一个隐藏的层。我们用n来表示这个隐藏层的神经元数量，我们将对n的不同值进行实验。这个例子展示了一个小的隐藏层，只包含n=15个神经元。
网络的输出层包含10个神经元。如果第一个神经元着火了，也就是说输出是1 ，这就表示网络认为数字是0。如果第二个神经元触发，那就意味着网络认为数字是1，等等。更准确地说，我们从0到9的输出神经元，并找出哪个神经元具有最高的激活值。如果这个神经元是6号神经元，那么我们的网络就会猜测输入的数字是6。对于其他输出神经元也是如此。

你可能想知道为什么我们要使用10个输出神经元。毕竟，网络的目标是告诉我们哪个数字（0,1,2，……，9）对应于输入图像。一种看似自然的方法是使用4个输出神经元，把每个神经元当作一个二进制值来对待，这取决于神经元的输出是否接近于0或1。四个神经元就够了，因为 24=16 2 4 = 16 比输入数字的10个可能值要多。为什么我们的网络应该使用10个神经元呢？这不是效率低下吗?最终的理由是经验性的：我们可以尝试两个网络设计，结果是，对于这个特殊的问题，拥有10个输出神经元的网络比拥有4个输出神经元的网络更能识别数字。但这让我们想知道为什么使用10个输出神经元会更好。是否有一些启发式方法可以提前告诉我们，我们应该使用10-输出编码而不是4-输出编码？

为了理解我们为什么要这样做，它有助于思考神经网络从最初的原理中所做的事情。首先考虑我们使用10个输出神经元的情况。让我们把注意力集中在第一个输出神经元上，这个神经元试图决定这个数字是否为0。它通过从隐藏的神经元层中权衡证据来做到这一点。那些隐藏的神经元在做什么？好吧，假设为了论证，隐藏层中的第一个神经元会检测到一个像下面这样的图像是否存在：

它可以通过重加权输入像素来实现这一点，它与图像重叠，并且只对其他输入进行轻微的加权。同样地，让我们假设，隐藏层中的第二、第三和第四神经元检测出下面的图像是否存在：

正如你可能已经猜到的，这四张图片组成了我们在前面所示的数字行中所看到的0图像：

所以如果所有这些隐藏的神经元都被激活了那么我们就可以得出这个数字是0。当然，这并不是我们可以用来得出结论的唯一证据，即图像是0—我们可以通过许多其他方式得到一个0（例如，通过对上述图像的翻译，或者轻微的扭曲）。但似乎可以肯定地说，至少在这种情况下，我们会得出结论，输入是0。
假设神经网络以这种方式运作，我们可以给出一个合理的解释，为什么从网络中得到10个输出，而不是4个。如果我们有4个输出，那么第一个输出神经元将会试图决定这个数字中最重要的位是什么。而且没有一种简单的方法可以将最重要的部分与简单的形状联系起来，就像上面所展示的那样。很难想象有什么好的历史原因，这个数字的组成部分将与（例如）输出中最重要的部分密切相关。
现在，有了这些，这都是一种启发式。没有什么能说三层神经网络必须像我描述的那样运作，隐藏的神经元检测简单的组件形状。也许一个聪明的学习算法会找到一些权重的分配，让我们只使用4个输出神经元。但作为一种启发，我所描述的思维方式非常有效，并且可以为您节省大量的时间来设计良好的神经网络架构。