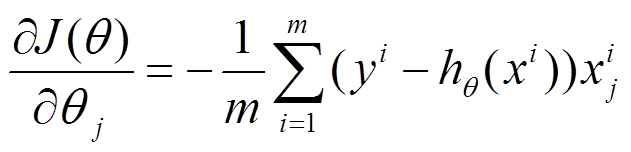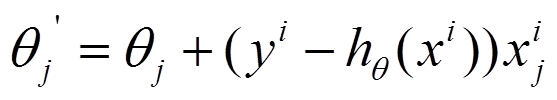加速神经网络的训练
为什么要加速神经网络
数据量太大,学习效率太慢
加速神经网络的方法
1、Stochastic Gradient Descent (SGD)随机梯度下降
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,其数学形式如下:
(1) 对上述的能量函数求偏导:
(2) 由于是最小化风险函数,所以按照每个参数的梯度负方向来更新每个:
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent,简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的能量函数写为如下形式:
利用每个样本的损失函数对求偏导得到对应的梯度,来更新:
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
2、Momentum 更新方法
在更新参数上(更新更快)做做手脚。
momentum是梯度下降法中一种常用的加速技术。对于一般的SGD,其表达式为,沿负梯度方向下降。而带momentum项的SGD则写生如下形式:
其中即momentum系数,通俗的理解上面式子就是,如果上一次的momentum(即)与这一次的负梯度方向是相同的,那这次下降的幅度就会加大,所以这样做能够达到加速收敛的过程。
通过增加参数,相当于让其处于一个梯度较大的方向,进一步缩小的更快。就相当于处于下坡路,不自觉都在下降。
3、AdaGrad 更新方法
在学习率上做手脚
当参数可能已经到了仅需要微调的阶段,但又有些参数由于对应样本少等原因,还需要较大幅度的调动。
Adagrad就是针对这一问题提出的,自适应地为各个参数分配不同学习率的算法。其公式如下:
其中 同样是当前的梯度,连加和开根号都是元素级别的运算。 是初始学习率,由于之后会自动调整学习率,所以初始值就不像之前的算法那样重要了。而是一个比较小的数,用来保证分母非0。
其含义是,对于每个参数,随着其更新的总距离增多,其学习速率也随之变慢。
相当于给人穿上膈脚的鞋子
4、RMSProp 更新方法
将上述两者形式稍加结合。
RMSProp通过引入一个衰减系数,让r每回合都衰减一定比例,类似于Momentum中的做法。
具体实现:
需要:全局学习速率 , 初始参数 , 数值稳定量,衰减速率
中间变量: 梯度累计量r(初始化为0)
每步迭代过程:
1. 从训练集中的随机抽取一批容量为m的样本,以及相关的输出
2. 计算梯度和误差,更新r,再根据r和梯度计算参数更新量
优点:
相比于AdaGrad,这种方法很好的解决了深度学习中过早结束的问题
适合处理非平稳目标,对于RNN效果很好
缺点:
又引入了新的超参,衰减系数
依然依赖于全局学习速率
5、Adam 更新方法
Adam 算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率(即 alpha)更新所有的权重,学习率在训练过程中并不会改变。而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。
Adam 算法的提出者描述其为两种随机梯度下降扩展式的优点集合,即:
-
适应性梯度算法(AdaGrad)为每一个参数保留一个学习率以提升在稀疏梯度(即自然语言和计算机视觉问题)上的性能。
-
均方根传播(RMSProp)基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。