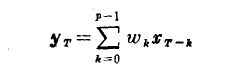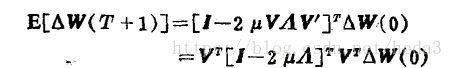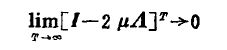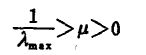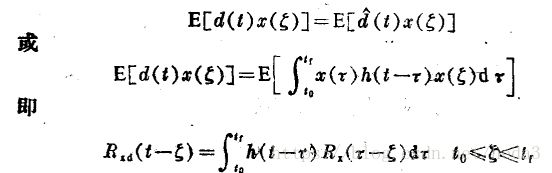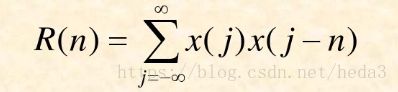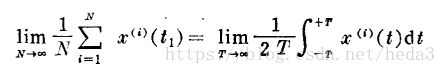自适应滤波-----LMS（Least Mean Square）算法

自适应滤波的意义所在

 

自适应滤波器解决非平稳的过程，因为实际信号的统计特性可能是非平稳的或者是未知的。

自适应滤波器的特点：

                                         1.没有关于待提取信息的先验统计知识

                                        2.直接利用观测数据依据某种判据在观测过程中不断递归更新

                                        3.最优化

自适应滤波分类：

处理器的结构划分：横向结构、格型结构

 重复一次计算自适应需要的数据划分：成批处理法、递归处理法

按调节算法划分：随机梯度和最小二乘

区分：ARMA 和MA模型   IIR和FIR

应用：

噪声抵消、回声抵消、谱线增强、通道均衡、系统辨识、时间延迟估计

算法的通俗解释：

 最小均方自适应滤波，通过两路信号，一路为参考信号d，另一路信号通过滤波器(H)估计出d',d'和参考信号d之间要满足均方误差最小的判据，而初始状态下滤波器系数设置为W(0),得到的结果d'不满足误差最小的判据，此时采用自适应优化算法去调节滤波器系数W，在不断的迭代计算后，找到这样的W*使得估计的d'和期望得到的d误差最小，而采取的最优化算法为随机梯度下降，也即是每进一个新数据x(t)求取它梯度并计算W，在这过程中x(t)和d(t)的误差是对应的。

可参考：比如取一段固定的信号去做滤波https://blog.csdn.net/HJ199404182515/article/details/52504150?locationNum=1没有考虑error满足一定的值

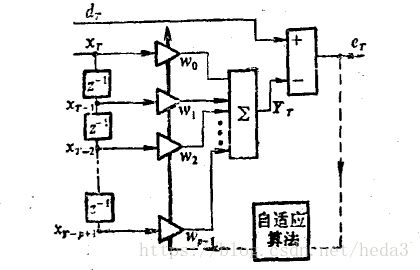
LMS算法的框架：

w0 w1...wp-1表示滤波器系数，xt....xt-p+1表示输入信号，dtT为参考信号（期望信号）此信号的选择很关键也是容易让人困扰的地方

Yt表示输入信号在滤波器作用下的输出响应，eT为参考信号和Yt的误差，即是et=dt-Yt；并依据误差et的大小调节滤波器系数w。

模型：

表示成矩阵的形式：yt

策略：

求误差函数值et最小时的系数w，即是et和W满足如下的函数关系式，求解函数值et最小时的解w：

假设最终求得的解是W*，那么在每次的迭代计算中如何逐次更新W？使它朝着离W*最近的方向前进，相当于要考虑使用什么样的算法来求解最优模型。

算法：

随机梯度下降算法实现最优化

关于梯度下降法分为：梯度下降、批量梯度下降和随机梯度下降，如何区分呢？

为了能找到最大下降的方向，可随机选取一个数据点求取梯度，或者是选取小批量的数据求取梯度，或者全部数据参与运算，此时有多个数据参与运算，计算量变大，但是求解的效果可趋向于全局解。

参考：https://blog.csdn.net/zbc1090549839/article/details/38149561

随机梯度特点是：单样本求得的梯度值代替真实梯度

递推公式

G（T）为求出的梯度（负值），随机梯度下降法求得的G（T）

所以得：

1、步长的选择很关键，选择过大会使得过程发散。为此步长需要满足如下的关系式：

构造：

Rx（正定对称自相关阵）：

则：

则：要使得上述式子趋近于0，
也即是求得的系数W不再变化（认为找到最合适的W值）

需要满足：

最终收敛条件是：

代码实现：（待续）

 

LMS的疑问：

期望信号是什么？

自适应处理解决的是随机信号的统计特性未知时，如何去自适应更新W系数达到过滤出想要的信号，其中W的解最终接近于维纳解W*，也就是说和维纳滤波的最终目的是一样的：实现一个处理器对信号进行过滤；只不过维纳滤波知道信号的统计特征，因此在后续滤波器的设计中依据这些统计特征即可一步到位的设计出处理器(H,也即是滤波系数或者是系统函数)；而自适应滤波采用的方法是增加一个期望信号d(t)（或者说参考信号更好一些），因此就有两路信号，这两路信号是有差别的，可能1路包含了噪声n(t)，第2路包含了噪声和想要的信号s(t)+n(t);，然后依据这两路信号的误差最小判据，并采用一定的优化算法去逐步的迭代计算，当满足误差在某一个最小值时，既可以求出W系数。

参考：1、https://blog.csdn.net/linj_m/article/details/14107763

2、https://blog.csdn.net/HJ199404182515/article/details/52504150?locationNum=1

3、https://blog.csdn.net/pi9nc/article/details/27310669

和维纳滤波器的区别？

维纳滤波器：已知信号波形的统计特性，构建对应的滤波器。适用于平稳随机过程，平稳也即是统计特性不随时间变化的随机过程。

1.维纳滤除算法的通俗解释：

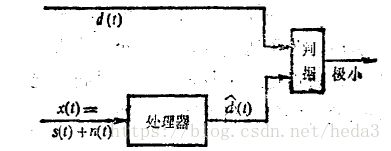
待处理信号x（t）包含真实信号以及噪声成分，现在希望提取的信息为d（t），因此需要设计一个处理器

使得估计值d'（t）在一个判据下取得极小值

为此有3个问题

1、怎么知道d（t）？

3、处理器应该怎么设计？

2、采用什么判据？

首先d（t）信号我们需要知道它的统计特性知识，即使信号波形本身可以不知道；然后d(t)的使用是为了后面的数学计算；

采用的判据是均方误差最小判据，并求解此策略最终的解需要d（t）的统计特性知识，例如d(t)本身的自相关、d(t)和x(t)互相关函数；最终求解出H，H本身就是最终需要设计的处理器。此后H不再改变。

其中

判据为：

处理器为：

 

相当于线性均方估计的引申

因此所用到的假设是：最优线性均方估计的选取需要使得估计误差e(t)与所有的x(t)正交；也即是如下公式

满足上式时使得均方误差最小

继续上面的问题：如何求解均方误差的函数式以得出处理器H？

依据正交原理和均方误差的判据可得出如下的维纳-霍夫积分方程：

只要知道Rxd和Rx，则上式的积分方程可求出h。

2.维纳滤波器具体分类

    非因果维纳滤波：需要时间轴上的全部信号知识

    因果维纳滤波  ：FIR型和IIR型 ，因果型即是只需过去的x(t)

后验维纳滤波：如果统计特性未知，那么首先需要估计信号的统计特性，再依据此设计维纳滤波器。

互补维纳滤波：在信号不是随机时的处理方法，采用H1和1-Hz互补方式

其中线性均方估计是：

 

【1】参考生物医学信号处理

【2】自适应滤波原理matlabcode http://www.pearsoninternationaleditions.com/Sitemap/Haykin/

补充数学知识：

奇异矩阵

问题：

 

答：由以上可知它是一个均值为0方差为1的白噪过程

则E(x)=0  D(x)=E{[x-E(x)]^2}=E(x^2)=1

而自相关函数离散形式

 则Rx(m-n)其中的m-n相当于上述的n。当m=n时Rx(m-n)=E(x^2)=1 否则R(m-n)=E(x1*x2)=E(x1)*E(x2)=0

数字特征的知识补充：

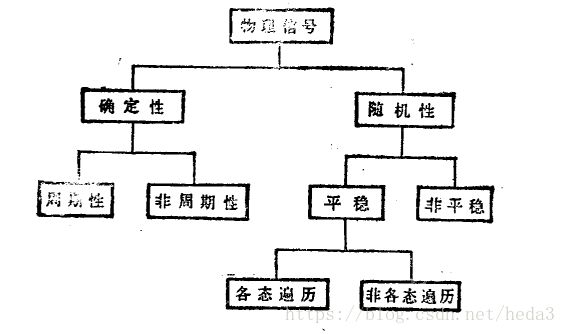
首先现实中的物理信号分为确定性信号和随机信号，如上图所示，确定性信号说明无论何时、何地观测，信号是有规律的，统计特性不变，能够准确的预测。随机信号则是随机变量在不同的时刻的值是不确定的，但是这个不同时刻的值具有一定的统计特性（下面要说的平稳信号）；其实现实中的信号如何区分确定信号和随机信号呢？

引用一句话：目前认为是随机性的事物，往往是因为现阶段还没有掌握影响该事物诸多因素所遵循的规律。

那断定为必然的东西，是由种种纯粹偶然所构成的，而被认为是偶然的东西，则是一种必然性隐藏在里面的形式！

区分平稳随机过程和非平稳？

首先信号是随机信号，且它的统计特性与进行分析的时刻无关，也即是说它的统计特性不随时间变化

区分弱平稳和强平稳？

弱平稳是：只有一阶、二阶统计特征具有平稳性，

强平稳是：任何阶的统计特征都是平稳的。

区分各态遍历性？

如公式所示：全部样本在某个固定时刻的统计特性=单个样本在全部时间上的统计特性 满足这个关系则称此信号具有各态遍历性

 

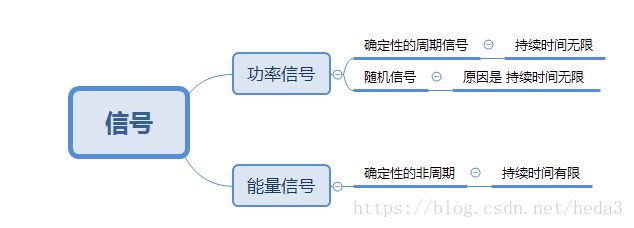
信号划分为：功率信号和能量信号

功率信号是：能量无限（持续时间无限），但是功率有限

能量信号：能量有限（持续时间有限）

注意：1、相关函数的傅氏变换等于功率