初学CNN from Hung-yi Lee 's ML
久违的学习笔记,在周围大佬们的陪(压)伴(力)下,不得不给自己学习的压力啊!
周五就要做报告了,得赶快写点总结。前面几课笔记周五补上,给自己挖个坑,记得填。废话不说,拿出朕的小本本开写。
CNN(Convolutional Neural Network)卷积神经网络
听名字就觉得很吓人,卷积什么的!
1. What’s CNN?
1.1 CNN定义
定义1. 一种专门用来处理类似网格结构的数据的神经网络。
eg:时间序列数据(一维网格)、图像数据(二维像素网格)
定义2:至少在网络的一层中使用卷积运算来替代一般的矩阵乘法运算的神经网络。
1.2 卷积 Convolution
卷积–对两个实变函数的一种数学运算
设x(t),w(t)是R1上的可积函数,则运算s(t)=(x*w)(t),被定义为卷积,*表示卷积。
其中一个参数叫做输入(input),一个参数叫做核函数(kernel function),一般输出叫做特征映射(feature map),核通常都是由学习算法得到的多维数组参数,称为张量。
2. Motivation & Property
2.1 Some patterns are much smaller than the whole image
对应特征–稀疏交互(sparse interaction)
通过让核的大小远小于输入的大小实现

比如说,需要让神经网络识别一只鸟。当然我们可以直接把这张图扔进一个全连接网络里,然后得到输出。但是,这样太没有效率了。假设说其中某一层隐藏层中的某一个神经元要识别鸟嘴,而要识别出一只鸟嘴,其实并不需要整张图,只需要含有鸟嘴的那一小块图就好了。在这儿,鸟嘴就是一个识别的pattern。
所以第一个motivation是,一般pattern远小于整张图。
传统的神经网络里,参数矩阵参数中,每一个单独的参数都描述了一个输入单元和一个输出单元间的交互。即每一个输出单元与每一个输入单元都产生交互。然而卷积神经网络并非如此,因此称为稀疏交互,后面会说到。
2.2
The same patterns appear in different regions
对应特征-参数共享(parameter sharing)
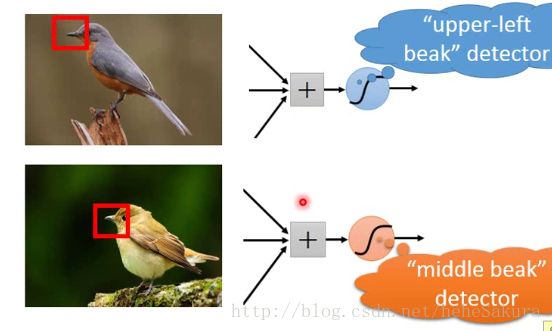
假设现在有两张有鸟的图,依然有识别鸟嘴这个任务。识别鸟嘴是做一样的事,不需要一个神经元检测左上角的鸟嘴,一个检测中间的鸟嘴。
所以就有了第二个motivation,相同的pattern出现在不同区域。
对应的特征叫做,参数共享,之后会具体解释。
2.3
Subsampling the pixels will not change the object
对应特征-等变表示(equivariant representation)

假设把纵轴奇数col拿掉,横轴奇数row拿掉,整张图变为原来的1/4,但还是能识别出是鸟。
所以这就对应了第三个motivation,即使把image做subsampling,还是不会能影响这张图像的识别。
3. The Whole CNN
3.1 一个典型的神经网络层的组件
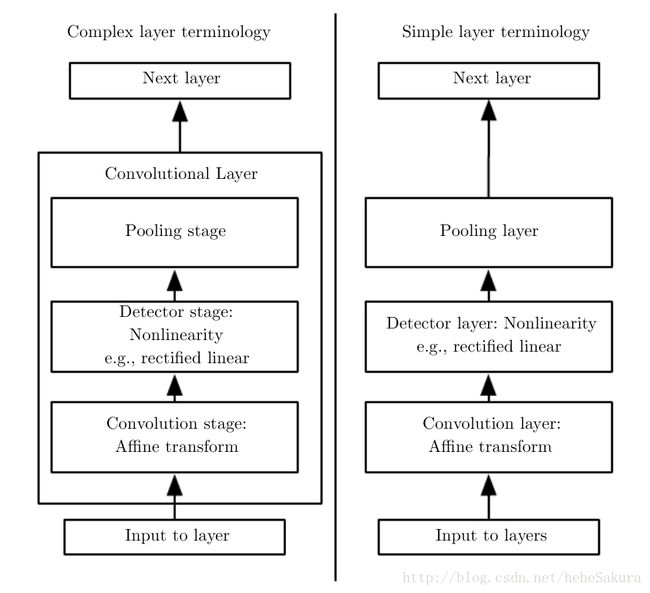
上图是一个典型的卷积神经网络层的组件。有两组常用的术语,对于左图:卷积网络被视为少量相对复杂的层,每层有许多级(stage)
- 第一级中并行得计算多个卷积产生一组线性激活响应
- 第二级中,每一个线性激活响应将会通过一个非线性的激活函数,上次有讲到说 ,激活函数是为了加入非线性因素,让NN能解决更复杂的问题
- 第三级使用pooling函数来进一步调整这一层的输出,有max pooling,mean pooling。
对于右图:卷积神经网络被视为更多数量的简单层,每个处理步骤都被认为是一个独立的层,意味着不是每一“层”都有参数。(什么叫做不是每一层都有参数?)
3.2 实例过程
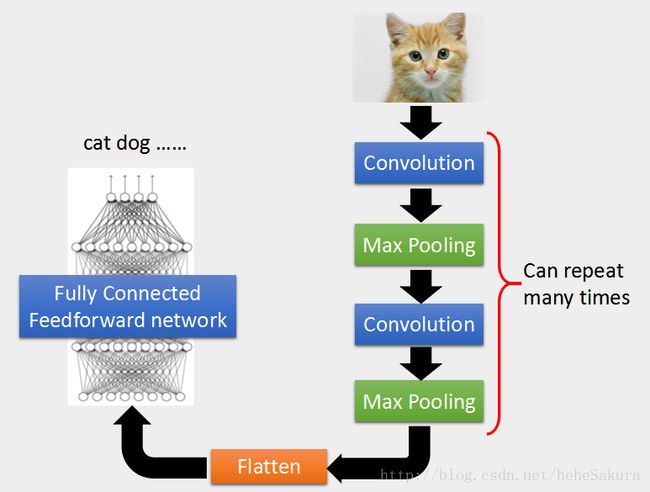
举一个栗子,输入一张image,先通过卷积运算,中间使用激活函数,再pooling,这三个过程可以反复做,然后flatten,再做输入到全连接网络,最后得到输出,即识别结果,猫、狗等等。
这整个过程的参数都是可以通过学习得到的,整套是同时一起被训练得到的。
- Motivation1.pattern远小于整张image。看小范围就能知道这个pattern是否出现,在卷积阶段会体现。
- Motivation2.同样的pattern出现在image的不同地方,只需要用同样的参数就可以侦测出来,也在卷积阶段体现。
- Motivation3.做pooling不会影响辨识结果,在pooling阶段体现。
3.2.1 CNN-Convolution
3.2.1.1 convolution是怎么做的呢
这个动图实在是太辣鸡了。开始录好屏,然后用格式工厂转成GIF,没想到变这么小,而且时间还被截短了。将就着看下面这一张图吧。
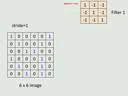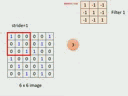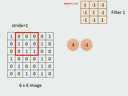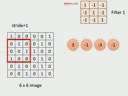
step1
- 输入一个image,6*6,每一个值代表一个像素
- 在convolution layer里,有很多filter,一个filter就是一个矩阵,里面的值是学习训练得到的,相当于fully
connected network里的weight - 假设已经知道filter的值,设置大小3*3。size体现了property1,pattern比image小,比3*3小
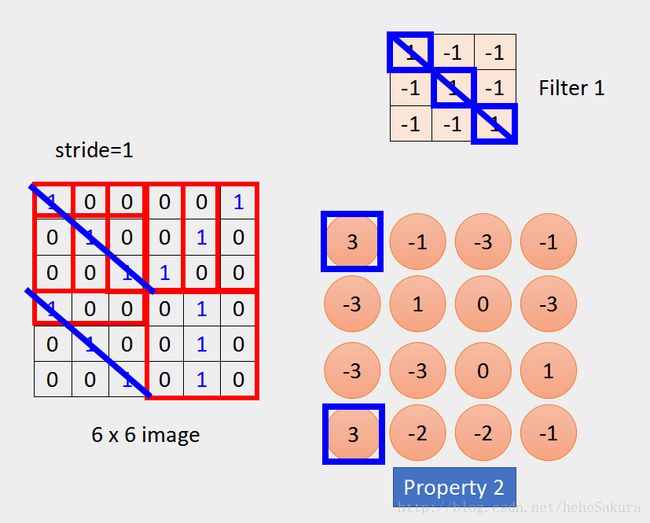
- 将filter放在image左上角,filter里的值和这个左上角盖住的9个值做內积,左上角对角线是111,其余是0,做內积就是3;
- 移动filter,移动的距离叫做stride 步长,然后平移得到-1;
以此类推得到整个一个新的矩阵
- filter斜对角是1,其实侦测的就是对角线是都为1的pattern,如果发现了就会输出较大的值
- 这个image左上角和左下角的小矩阵里对角线都是111,因此得到新的matrix对应的值很大,就显示说这个image里有两个这个filter对应的pattern
- 同时这里也响应了前面说的property2,在image的不同位置,同样的pattern都是用同一个filter找到的
step2
- 假设还有第二个filter
- 做同样的操作,因为filter参数不同,得到不同的结果
- 得到的输出叫做feature map,相当于一张新的image,比原来的小,因为filter考虑的范围从image的左上角到右下角
- 新的image,每个像素用的更多的值来描述
- 原来黑白的image,每个像素是一个数值,但新的image里,有两个值进行描述,取决于有几个filter
3.2.1.2 如果是彩色的图

每个像素由三个数值描述RGB,红蓝绿的强度,都分别称为channel,所以彩图有三个channel。做convolution时,filter是相当于是一个立方体,3*3*3,前面3*3是filter大小,最后一个3是3个channel,一共就有27个参数。
3.2.1.3 CNN v.s. Fully Connected Network
CNN可以看做是全连接网络的简化版。将feature map拉直可以看做是全连接网络里的输出神经元。
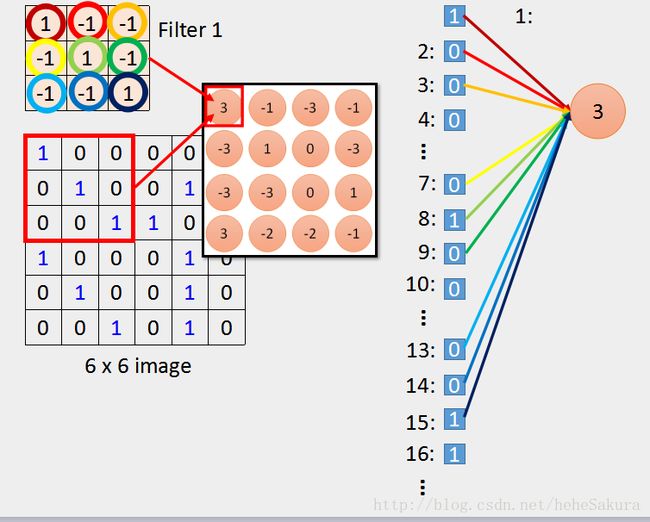
做convolution的时候,用filter中的9个值和image中对应的数做內积得到
- 可以看成image的像素拉直,像素矩阵里第一行的1,0,0
…对应直立的编号1,2,3…对应的值1,0,0…;第二行的0,1,0…
,就是直立的编号7,8,9…对应的值0,1,0… - featuremap输出的第一个3,相当于是编号1,2,3,7,8,9,13,14,15得到,filter就相当于是weight,用同样的颜色进行了标注
- 原来的全连接网络会将每一个输入都连接到神经元,然而这里只有九个输入值,连接到这一个神经元
- 每一个输入单元只与部分输入单元产生交互,这就是前文提到的第一个特征,稀疏交互。这样的操作也减少了参数。

feature map 的第二个值-1,也是同样的方式,这其中使用了同一组weight,即前文提到的第二个特征,参数共享。相比全连接网络里的每一个参数都是同时学习得到,进一步减少了参数。
3.2.2 CNN-Pooling
Pooling释义
使用池化函数(pooling function)对某一位置的相邻输出的总统计特征来代替网络在该位置的输出。有max pooling、mean pooling。
最近看论文,涉及到了对graph data做pooling。当时我又懵逼了,一时无法理解为什么要pooling。原来是因为经过激活函数处理之后的输出仍然很多。而且就图像而言,图像的特征有一种静态性,因此需要将特征进行统计处理。max pooling和mean pooling都能够很大程度上保持、统计特征。所以,基于特征统计、减少计算的目的诞生了CNN的pooling。
举例
接着上述的那个例子,接下来做max pooling
通过filter得到两个新矩阵,把matrix里的分组,假设分组为2*2,选出其中个每个最大值,就是max pooling。
最后求参数的时候,会用到梯度下降,用maxout network。这里就不细说了。
最大池化引入不变性
- 上图,卷积层中间输出的视图,下面一行是激活函数的输出,上面一行是最大池化的输出。每个池的宽度为三个像素,即上一页说的分组,且stride设为1。
- 下图,相同视图中,对输入右移了一个像素,下面一行的每一个值都变了,但是上面一行只有一半的值改变了,这是因为最大池化单元只对周围的最大值比较敏感,而不是对精确的位置。
意义
当关注某个特征是否出现,而非出现的具体位置时
eg.图像中是否含有人脸
Convolution->Max Pooling->
- 通过convolution之后,在做max pooling,得到比上一个image还要小的image。
- 可以反复做多次
3.2.3 CNN-Flatten
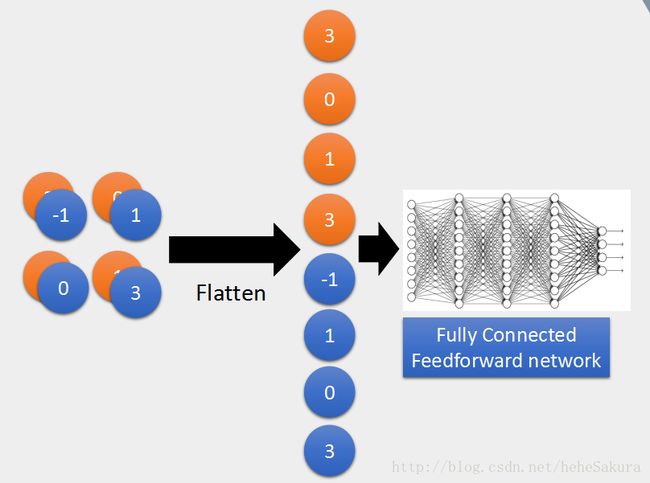
- 当最后pooling得到image差不多了,就做flatten,将image里每个像素里每个channel的值拉直
- 经过几次convolution、pooling之后,参数减少,经过flatten拉直的就不会太长,然后放入全连接网络里,就可以得到输出
- 训练可以用梯度下降
4. Summary
CNN有3个属性
稀疏交互、参数共享、等变表示
CNN的过程
与Fully Connected Network 的比较
- CNN可以看做是一个简化版的全连接网络。
- CNN的卷积层中每一个输出单元只与部分输入单元产生交互,同时存在权值共享,因此比全连接网络参数少之又少。
5. Reference
http://scs.ryerson.ca/~aharley/vis/conv/ 卷积神经网络3D视觉化模型
Ian Goodfellow, Yoshua Bengio, and Aaron Courville,Deep Learning,2016
Hung-yi Lee Machine Learning
博客里的很多图取自李宏毅的ML课件,以及Deep Learning书中的插图。
初学肯定有很多写的不准确或不对的地方,请大家指出,互相进步(^▽^)