机器学习线性回归（linear regression）/梯度下降法（gradient descent)/最大似然函数/--附python代码

本文为吴恩达《机器学习》课程的读书笔记，并用python实现。

线性回归是一个比较简单的算法，这里主要借线性回归，讲一下梯度下降法和最大似然函数，后面逻辑回归也会用到。
因为不能粘贴公式，所以很多内容直接截屏，不是很美观。

机器学习主要分为两种：
1. 有监督学习（supervised learning）：即常说的分类（classification）和回归（regression），通过训练样本集（包含输入和输出），得到一个最优模型，再利用这个模型将所有的输入映射为相应的输出，对输出进行简单的判断从而实现分类的目的，也就具有了对未知数据进行分类的能力。
监督学习里典型的例子就是KNN、SVM
2. 无监督学习（unsupervised learning）：我们有一些问题，但是不知道答案，我们要做的无监督学习就是按照他们的性质把他们自动地分成很多组，每组的问题是具有类似性质的。
无监督学习里典型的例子就是聚类。
线性回归属于监督学习。
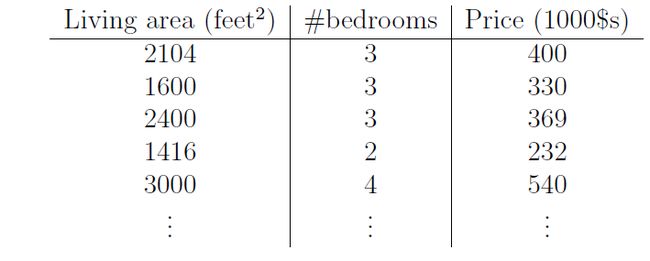
首先我们看下这么一个例子，假设我们有47套房子的面积和价格数据：

我们可以将图画出来：

有了这些数据，我们如何去学习他们，然后根据别的房子的面积来预测价格呢？
首先，让我们做如下定义，方面后面的讨论：

下面更加正式的定义监督学习问题，我们的目标是：给定一个训练集，得到一个从输入映射到输出的函数h，如下图所示。

当我们要预测的目标变量是一个连续的值，比如房子的价格，我们称这个问题为回归（regression），当y只能取很少几个值（比如给定房子的面积，我们想要预测这个房子是居住房还是公寓），我们称之为分类（classification）。

第一部分 线性回归
考虑如下数据集：



1 最小均方（LMS）算法（least mean squares）

附LMS算法步骤：
1、设置变量和参量：
X(n)为输入向量，或称为训练样本
W(n)为权值向量
e(n)为偏差
d(n)为期望输出
y(n)为实际输出
η为学习速率
n为迭代次数
2、初始化，赋给w(0)各一个较小的随机非零值，令n=0
3、对于一组输入样本x(n)和对应的期望输出d，计算
e(n)=d(n)-X^T(n)W(n)
W(n+1)=W(n)+ηX(n)e(n)
4、判断是否满足条件，若满足算法结束，若否n增加1，转入第3步继续执行。

1.1批处理下降法（batch gradient descent）

1.2 增量梯度下降法（incremental gradient descent）
增量梯度下降法（incremental gradient descent）也叫做随机梯度下降法（stochastic gradient descent），与批处理梯度下降法不同的是，每次根据一个训练样本就更新 ，具体如下：

2 正规方程组求解（The normal equations）

3 用最小均方作为代价函数的概率解释
当我们面对线性回归的时候，为什么用最小均方最为代价函数（cost fuction，下式）是合理的呢？



4 局部加权线性回归（locally weighted linear regression）
参数学习方法：在训练完成所有数据后得到一系列训练参数，然后根据训练参数来预测新样本的值，这时不再依赖之前的训练数据了，参数值是确定的。
非参数学习方法：在预测新样本值时候每次都会重新训练数据得到新的参数值，也就是说每次预测新样本都会依赖训练数据集合，所以每次得到的参数值是不确定的。
局部加权线性回归是非参数学习方法。

python 代码：
#author: lijiayan
#date:2016/10/27
from numpy import *
import matplotlib.pyplot as plt

def loadData(filename):
data = loadtxt(filename,delimiter=',')
x = data[:,0:1]
y = data[:,1:2]
return x,y


#the cost function
def costfunction(y,h):
J = (1/2.0)*sum(y-h)**2
return J


# the batch gradient descent algrithm
def gradescent(x,y):
m,n = shape(x)      #m: number of training example; n: number of features
x = c_[ones(m),x]     #add x0
x = mat(x)      # array to matrix
y = mat(y)
a = 0.0001       # learning rate
maxcycle = 1400
theta = zeros((n+1,1))    #initial theta

J = []
for i in range(maxcycle):
    h = x*theta
    theta = theta + a * x.T*(y-h)
    cost = costfunction(y,h)
    J.append(cost)

plt.plot(J)
plt.show()
return theta,cost


#the stochastic gradient descent (m should be large,if you want the result is good)
def stocGraddescent(x,y):
m,n = shape(x)      #m: number of training example; n: number of features
x = c_[ones(m),x]     #add x0
x = mat(x)      # to matrix
y = mat(y)
a = 0.0002       # learning rate
theta = ones((n+1,1))    #initial theta

J = []
for i in range(m):
    h = x[i]*theta
    theta = theta + a * x[i].T*(y[i]-h)
    cost = costfunction(y,h)
    J.append(cost)
plt.plot(J)
plt.show()
return theta,cost

#plot the decision boundary
def plotbestfit(x,y,theta):
plt.plot(x,y,'x')
x = arange(5,25,0.1)
y = float(theta[1])*x+float(theta[0])

plt.plot(x,y)
plt.xlabel('x')
plt.ylabel(('y'))
plt.show()


#predict the output y for the new input inX
def classifyVector(inX,theta):
y = inX*theta
return y


if __name__=='__main__':
x,y = loadData("ex1data1.txt")
theta,cost = gradescent(x,y)
print 'theta=:',theta
print 'J=:',cost

X = [1,5]     #new input
print 'X:',X
print 'predict y is:',classifyVector(X,theta)

plotbestfit(x,y,theta)

由于数据是一个m=100的训练集，训练样本少，所以用增量梯度法没法收敛，这边用了批处理梯度下降法，下面是结果：