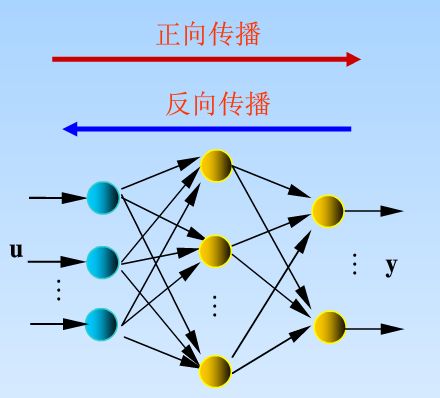
前向型神经网络之BPNN(附源码)
BPNN
人工神经网络
我们知道,人的脑袋具有很强的学习、记忆、联想等功能,虽然人类还没有完全搞明白人类的大脑,但是我们已经知道它的基本单位就是一个个神经元,即一个神经细胞,人的神级细胞个数大约为 1011 个,海兔大约为2000多个,数目越多就越复杂,处理信息的能力就越强。如下图所示,每个神经元由细胞体与突起构成,细胞体的结构与一般的细胞相似,包括细胞膜,细胞质与细胞核,突起是神经元胞体的延伸部分,按照功能的不同分为树突与轴突。树突的功能是接受冲动并将冲动传入细胞体,即接受其它神经元传来的信号,并将信号传给神经元它是传入神经末梢。而轴突将本神经元的冲动传递给其它的与之相连的神经元,因此它是输出神经末梢。
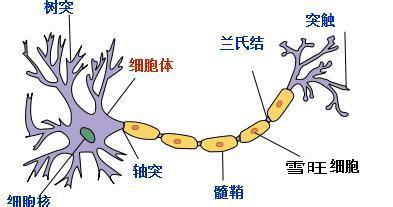
大脑的神经元便是通过这样的连接进行信号传递来处理信息的,每个神经元通过其接受的信号来使得其兴奋或抑制。神经元内部信号的产生、传导采用电信号的方式进行,而神经元之间、神经元与肌肉之间则通常采用化学递质方式进行传导,即上级神经元的轴突在有电信号传递时释放出化学递质,作用于下一级神经元的树突,树突受到递质作用后产生出点信号,从而实现了神经元间的信息传递。而神经元的兴奋与抑制是由接受到的递质决定,有些递质起兴奋作用,有些起抑制作用。当传入神经元的冲动经整合,使细胞膜电位升高,超过动作电位的阈值时,为兴奋状态,产生神经冲动,由轴突神经末梢传出。当传入神经元的冲动经整合,使得细胞膜电位降低,低于阈值时,为抑制状态,不产生神经冲动。
大脑可通过自组织、自学习,不断适应外界环境的变化。大脑的自组织、自学习性,来源于神经网络结构的可塑性,主要反映在神经元之间连接强度的可变性上。由于神经元结构的可塑性,突触的传递作用可增强与减弱,因此神经元具有学习与遗忘功能。
人工神经网络起源于上世纪40~50年代,它是在基于人脑的基本单元-神经元的建模与联结,模拟人脑神经系统,形成一种具有学习、联想、记忆和模式识别等智能信息处理的人工系统,称为人工神经网络(Artificial Neural Networks,简称ANN),它是一种连接模型(Connection Model)。1943年神经生物学家MeCulloch与青年数学家Pitts合作,提出了第一个人工神经网络模型,并在此基础上抽象出神经元的数理模型(即神经元的阈值模型,超过阈值则兴奋,否则抑制),被称为MP模型(名字命名),这是ANN的启蒙阶段,ANN正式进入研究阶段。1958年Rosenblatt在原有的MP模型的基础上增加了学习机制,他提出的感知器模型,首次把神经网络理论付诸于工程实现,ANN研究迎来第一次高潮期。1969年出版的轰动一时的《Perceptrons》一书指出简单的线性感知器的功能是有限的,它无非解决线性不可分的而分类问题,如简单的线性感知器不能实现“异或”的逻辑关系,加上神经网络就和黑夹子一样,很多东西不透明,模型的解释性不强,参数过多,容易出错,容易过拟合,无法保证全局最优等问题,同时70年代集成电路和微电子技术的迅猛发展,使得传统的Von Neumenn计算机进入全盛时期,基于逻辑符号处理方法的人工智能得到了迅速发展并取得了显著的成果。ANN进入了长达10年的低潮期。1982年,美国科学院发表了著名的Hopfield网络模型的理论,不仅对ANN信息存储和提取功能进行了非线性数学概括,提出了动力方程和学习方程,使得ANN的构造与学习有了理论指导。这一研究激发了ANN的研究热情。1986年,由Rumelhat和McChekkand等16位作者参加撰写的《Parallel Distributed Processing: Exploration in Microstructures of Cognition》一书,建立了并行分布式处理理论,并提出了BP算法,解决了长期以来ANN中的权值调整问题没有有效解决方法的难题,可以求解感知器所不能解决的问题,回答了《Perceptrons》一书中关于神经网络局限性的问题,从实践中证实了ANN的有效性。BP算法产生了深远而广泛的影响,从至ANN的研究进入了蓬勃发展期。后来学者与研究者们又不断提出了RNN(Recurrent Neural Networks,递归神经网络)以及Deep Learning(深度学习)等模型。
本文主要对前向神经网络中的BP网络进行讲解.
人工神经网络拓扑结构
ANN使对大脑信息处理机制的模拟,是由大量简单的神经元广泛地互相连接而形成的复杂网络系统。它反映了人脑功能的许多基本特性,但它并不是人脑神经网络系统的真实写照,人脑神经系统比ANN要复杂地多,而ANN只是对其作某种简化抽象和机制模拟。ANN的目的在于探索人脑加工、存储和处理信息的机制,进而研制基本具有人类智能的机器。ANN是一个高度复杂的非线性动力学系统。虽然每个神经元的结构和功能十分简单,但大量神经元构成的网络系统的功能是强大的,能够以任何精度去逼近线性与非线性函数.
ANN中的每一个节点作为一个神经元,是对生物神经元的仿照,如下图:
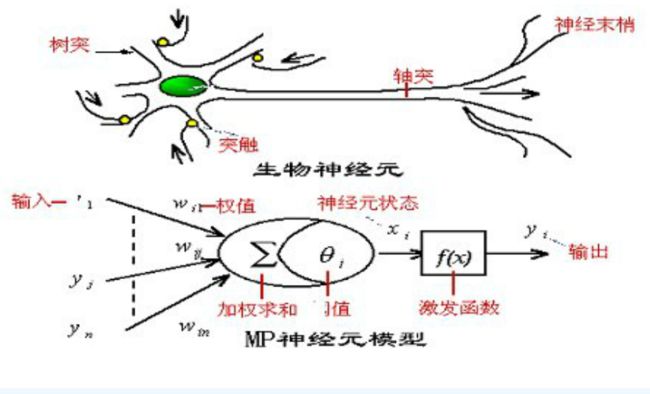
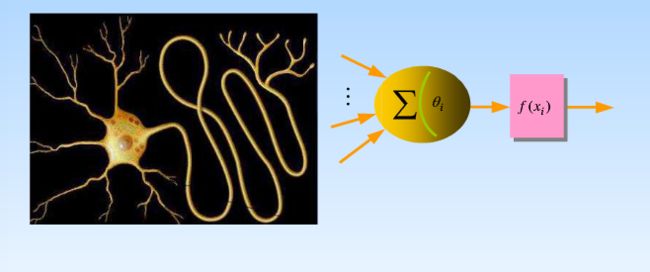
神经元 i 的输入为 y=(y1,...,yn) ,输出为 yi ,通过在神经元加权求和作用于激活函数再输出:
其中 f 为激活函数. 每一神经元的输出为0或1,表示“抑制”或“兴奋”状态. 具体根据使用的激活函数而定.
上面是一个神经元的结构与原理,那么将多个神经元排列组成便得到了ANN的结构,如图:
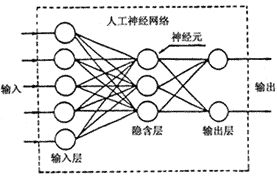
人工神经网络一般包含输入层、隐含层与输出层这三层结构,其中隐含层可包括多层,如下图二层隐藏层神经网络:
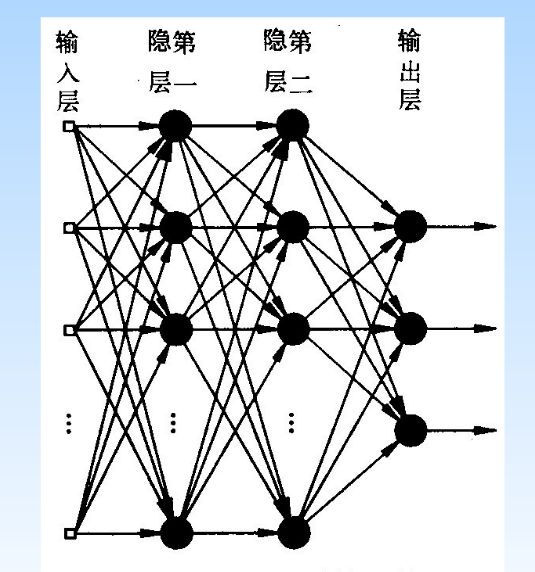
相同层之间的节点无连接,层与层之间的节点采用全连接结构,输入层对于输入的元素不作任何处理,即经输入层节点的输入与该节点输出相同,除了输入层的节点外的节点都有一个激活函数,这些节点的每个节点都对输入矢量的各个元素进行相应的加权求和,然后使用激活函数作用于上面作为输出。
那么网络便可简化为输入、权值、偏置、输出矩阵:
其中 W 矩阵与 b 向量均有有 T−1 个, T 为网络的层数. 网络节点之间的连接强度通过连接权值来反映.
激活函数
除了输出层节点外,每个节点都有一个激活函数,常用的激活函数如下 :
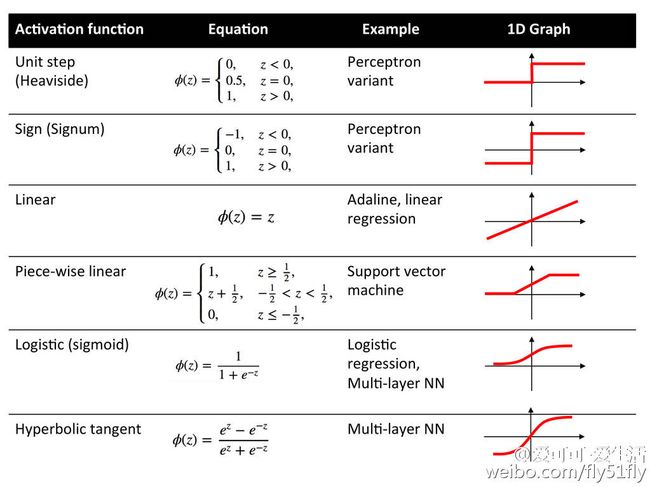
神经网络的类型
神经网络可分类以下四种类型:
- 前向型
BP前向神经网络是中广为应用的一种网络,其原理与算法也是某些其它网络的基础,除此之外还有辐射基函数(RBF)神经网络. - 反馈型
Hopfield神经网络用于非线性动力学问题分析,已在联想记忆和优化计算中得到成功的应用. - 随机型
具有随机性质的模拟退火(SA)算法解决了优化计算过程陷于局部极小的问题,并已在神经网络的学习及优化计算中得到成功的应用. - 竞争型
竞争型网络的特点是能识别环境的特征,并自动聚类。广泛用于自动控制、故障诊断等各类模式识别中.
神经网络的学习方法
当一个神经网络的拓扑结构确定之后,为了使它具有某种职能特性,必须对它进行训练。通过向环境学习获取知识并改进自身性能时神经网络的一个重要特点。学习方法归根结底就是网络连接权值的调整方法,修改权值的规则称为学习算法。学习方式(根据环境提供信息量的多少)包括:
- 监督学习(有教师学习)
这种学习方式需要外界存在一个”教师”,它可对给定一组输入提高应有的输出结果,这组已知的输入输出数据称为训练样本集,网络可根据已知输出与实际输出之间的差别来调节网络参数. - 无监督学习(无教师学习)
无监督学习顾名思义就是没有教师进行指导的学习,网络完全按照环境提供数据的某些统计规律来调节自身参数货结构(这是一种自组织过程),以表示出外部输入的某种固有特性,如聚类或某种统计上的分布特征. - 再励学习(强化学习)
这种学习方式介于前面所讲的两种学习方式之间,外部环境对系统输出结果只给出评价信息(奖或罚)而不是给出正确答案. 学习系统通过强化那些受奖的动作来改善自身的性能.
下面对多层前馈网络的一种学习方法,即反向误差传播算法,进行讲解.
BP算法原理
BP全称为Back Propagation,意思为反向传播,该方法是用来对人工神经网络进行优化的,即误差反向传播算法。
它属于有教师指导的学习方式。包括两个过程:
假设训练样本空间 Ω 中有 n 个训练样本,分别为 Si={xi1,...,xim,ŷ i1,...,ŷ il},i=1,...,n ,样本 i 通过神经网络后的输出值(即预测值)为 yi={yi1,...,yil} ,第 i 个训练样本的特征向量 xi 维度为 m ,预测值向量 yi 与真实值向量 ŷ i 向量维度均为 l .
假设神经网络有T层结构,其中第1层为输入层,第T层为输出层,第2到第T-1层为隐藏层,第t与第t+1层之间的连接权值矩阵为 Wt=[wtst×st+1],t=1,...,T−1 ,第t与第t+1层之间的偏置值为 bt=(bt1,...,btst) ,其中 st,st+1 分别表示第 t 与 t+1 层节点的个数.
BP算法使用梯度下降算法对网络中的各权值进行更新,如果使用批量更新算法,设batch的大小为p,采用平方误差和计算公式,那么一次batch的总误差为:
其中式中的 12 是为了计算方便. 一般我们使用平均平方误差和作为目标函数,即目标函数为:
按照梯度下降公式,每一次batch对各层之间的连接权值与偏置的更新方程为:
其中 α∈(0,+∞) 为学习速率, i 表示第 t 层的第 i 个节点, j 表示第 t+1 层的第 j 个节点.
因此神经网络的求解便落在求解连接权值矩阵 W 与偏置值 b 上面,通过梯度下降算法,我们需要求取 wtij 与 btj 的偏导数.
因为:
设
其中 yij 表示第 i 个训练样本的预测值的第 j 个分量, fT 表示第 T 层的激活函数,可以是sigmoid函数也可以是tanh函数等. T−1 表示网络的第 T−1 层, sT−1 表示第 T−1 层的节点的个数, oT−1ik 表示第 i 个训练样本在第 T−1 层第 k 个节点的输出值, wT−1kj 表示 T−1 层第 k 个节点到 T 层第 j 个节点之间的连接权值, ITij 为第 i 个训练样本时第 T 层第 j 节点的输入, ()′ 表示向量的转置.
那么对于最后一层隐藏层与输出层之间的连接权值矩阵与偏置向量,有:
对于sigmoid函数 f′=f(1−f) ,对于tanh函数 f′=1−f2 .
令
那么第 T−1 到第 T 层之间的连接权值矩阵与偏置值更新方程为:
对于第 T−2 到第 T−1 层之间:
令
那么第 T−2 到第 T−1 层之间的连接权值矩阵与偏置值更新方程为:
那么第 t 到第 t+1,1≤t≤T−2) 之间的连接权值矩阵与偏置值均按照上面的方程进行更新。
第 i 个样本在第一层(输入层)的输出 o1ik 即为第 i 个样本输入矢量的第 k 个输入分量,即为 xik .
算法步骤
- 首先使用随机函数对每一层间的连接权值矩阵和偏置向量进行随机初始化.
- 依次使用一个训练样本对网络进行训练,并按照上面的公式计算每个样本的 Δti,t=1,...,T−1
- 训练 p 个样本后(一次batch),按照更新方程对 W 与 b 进行更新.
- 重复步骤2~3,直到误差小于设定的阈值或者达到设定的batch次数.
BP学习算法相关问题
- 实现输入/输出的非线性映射
若网络输入、输出层的节点个数分别是m、l个,那么该网络实现了从m维到l维欧式空间的映射:
T:Rm→Rl
可知网络的输出是岩本输出在 L2 范数意义下的最佳逼近. 通过若干简单非线性处理单元的复合映射,可获得复杂的非线性处理能力. - BP学习算法的数学分析
BP算法使用梯度下降法进行参数优化,把一组样本的I/O问题,变味非线性优化问题,隐含层使优化问题的可调参数增加,使解更精确. - 全局逼近网络
BP网络时全局逼近网络,即 f(x) 在 x 的相当大的域为非零值. - 学习步长 α
α,0<α 称为学习步长,又称学习算子,值越大,权值调整得越快,在不导致振荡的情况下, α 可大一些. - 改进的BP算法
因为使用梯度下降法进行参数优化,而梯度下降算法不足之处就在算法收敛慢,为了克服这个缺点,可以:
- 带阻尼项的权值调整算法
为了使学习速率足够大,又不易产生振荡,在权值更新方程中,加上阻尼项:
wtij(p+1):=wtij(p)−α∂F∂wtij+β[wtij(p)−wtij(p−1)]
btj(p+1):=btj(p)−α∂F∂btj+β[btj(p)−btj(p−1)]
其中 β,0<β<1 为阻尼系数. - 变步长算法: α:=α/λ(i) 即随着训练的进行,步长逐渐缩小.
- 带阻尼项的权值调整算法
- 网络的输入
S 型作用函数 f(x) 随 |x| 的增大,梯度下降,即 |f′(x)| 减小,并 →0 ,不利于权值的调整. 于是我们希望 |x| 取值范围在较小的靠近0的范围内,因此网络的输入需要根据情况进行处理,如果网络的输入绝对值较大,那么需作归一化处理,此时网络的输出也要进行相应的处理. - 泛化能力
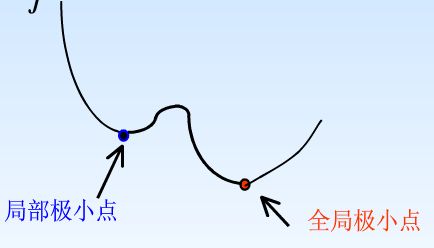
泛化能力:用较少的样本进行训练,使得网络能在给定的区域内达到要求的精度. 没有泛化能力的网络是没有实用价值的. BP网络的泛化能力与样本、网络结构、初始权值等有关,为得到较好的泛化能力,训练网络需要训练样本集外还需要测试集.下图为泛化能力示意图:
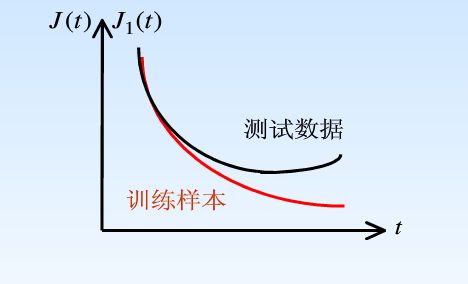
从上图可以看出,随着训练次数的增加,训练集的 J(t) 会减少,测试集的 J1(t) 可能不减少或增大,说明泛化能力减弱. 因此,可取测试集 J1 的极小点对应的训练次数,以使网络具有较好的泛化能力. - BP算法的不足
网络结构的设计
- 网络层数
目前已有相关理论证明:具有偏置和至少一个S型隐含层加上一个线性输出层的网络,能够逼近任何有理函数. 这实际上已经给了我们设计BP网络的原则:应优先考虑增加隐含层中的神经元节点个数而不是增加隐含层的层数. 增加层数主要是为了进一步降低误差,提高精度,但同时也使网络复杂化,从而增加了权值的训练时间. 而误差精度的提高实际上也可以通过增加隐含层中的神经元数目来获得,其训练效果也比增加层数更容易训练和调整. - 每层的神经元个数
网络训练精度的提高,可以通过采用一个隐含层,而增加其神经元数的方法来获得. 在这结构实现上,要比增加更多的隐含层要简单得多. 那么究竟选取多少个隐含层节点才合适,目前并没有明确地指导. 通常采用的做法是对不同数目的进行训练对比,然后适当加上一点余量. - 激活函数的选择
有多个激活函数可供选择,具体选择哪一个则需要根据实际的问题进行选取. 其实激活函数说不上谁比谁好,对于隐含层的激活函数,可以选择sigmoid、tanh、relu等多种激活函数. 而对于输出层的激活函数,则是有一定选择的:如果是两类分类问题,输出层只有一个神经元,那么选择sigmoid(logistic); 如果是n类分类问题,则输出层有n(或n-1)个神经元,那么选择softmax;如果是回归问题,那么选择线性激活函数. - 初始权值
由于系数是非线性的,初始值对于学习是否达到局部最小、是否能够收敛以及训练时间的长短的关系很大. 如果初始值太大,使得加权后的输入和sum落在S型激活函数的饱和区,从而导致其导数非常小,而在计算权值修正公式中,导数 →0 ,使得 ΔW→0 ,从而使得调节过程几乎停顿下来. 所以一般总是希望经过初始加权后的每个神经元的输出值都接近于零,这样可以保证每个神经元的权值都能够在它们的S型激活函数变化最大之处进行调节. 所以,一般取初始值在(-1,1)之间的随机数. - 学习速率
学习速率决定每一次batch训练中所产生的权值更新量. 大的学习速率可能导致系统的不稳定; 但是小的学习速率导致较长的训练时间,可能收敛速度慢,不过能保证网络的误差值不跳出误差表面的低谷而最终趋于最小误差值. 所以一般情况下,倾向于选取较小的学习速率以保证系统的稳定性,选取范围一般在[0.01, 1]之间.
在对神经网络的结构进行设计时,需要经过几个不同的学习速率的训练,通过观察每一次训练后的误差平方和的下降速率来判断所选定的学习速率是否合适. 如果误差平方和下降很快,则说明学习速率合适,若误差平方和出现振荡现象,则说明学习速率过大. 对于较复杂的网络,在误差曲面的不同部位可能需要不同的学习速率. 为了减少寻找学习速率的训练次数以及训练时间,比较合适的方法是采用变化的自适应学习速率,使网络的训练在不同的阶段自动设置不同大小的学习速率.
我们可以根据误差变化的信息对学习速率进行启发式调整:
- 若总误差E减小,则学习速率增加,比如将值放大1.1倍;
- 若总误差增加,则学习速率减小. 当新误差与老误差之比超过一定值(如1.1),则学习速率快速下降,如缩小到0.7倍.
- 期望误差的选择
在网络的训练误差减小到事先设定的期望误差时,则人为网络收敛. 因为要达到较小的期望误差值则要靠增加隐含层的节点,以及训练时间来获得. 一般,可以同时对两个不同的期望误差值的网络进行训练,最后通过综合因素考虑来确定采用其中哪一个网络.
算法源码
'''
该网络中隐含层所有的偏置项使用在输入层增加一个节点(节点输入输出值恒为1.0来代替),而输出层没有偏置项
@author hy
'''
import numpy as np
'''
激活函数类
'''
class Sigmoid:
#sigmoid函数
def f(self,x):
return 1/(1+np.exp(-x))
#sigmoid函数的导数
def df(self,x):
y = self.f(x)
return y-np.multiply(y,y)
class Tanh:
#双正切函数
def f(self,x):
return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
#双正切函数的导数
def df(self,x):
y = self.f(x)
return 1-np.multiply(y,y)
'''
工具类
'''
class Utils:
def uniform_distribution(self,x1,x2):
return np.random.uniform(x1,x2)
def create_random_matrix(self,row,col,periphery):
m = np.zeros((row,col))
for i in range(row):
for j in range(col):
m[i][j] = self.uniform_distribution(-1*periphery, periphery)
return m
def create_matrix(self,row,col,init_value=None):
m = np.zeros((row,col))
if init_value is not None:
for i in range(row):
for j in range(col):
m[i][j] = init_value
return m
def matrix_fill_zeros(self,m):
return np.zeros(np.shape(m))
'''
BP神经网络类
输入层、隐含层、输出层三层网络结构
'''
class BPNN:
#网络初始化
def __init__(self,input_node_num,hidden_node_num,output_node_num):
#输入层节点个数,增加一个偏置项
self.i_n = input_node_num+1
#隐含层层节点个数
self.h_n = hidden_node_num
#输出层节点个数
self.o_n = output_node_num
self.utils = Utils()
#输入层的输入(第i个样本),增加的偏置项节点的输入输出恒为1
self.i_i = self.utils.create_matrix(self.i_n,1,1.0)
#隐含层对第i个样本的输入
self.h_i = self.utils.create_matrix(self.h_n,1,0.0)
#输出层对第i个样本的输入
self.o_i = self.utils.create_matrix(self.o_n,1,0.0)
#输入层的第i个样本输出,增加的偏置项节点的输入输出恒为1
self.i_o = self.utils.create_matrix(self.i_n,1,1.0)
#隐含层对于第i个样本的输出
self.h_o = self.utils.create_matrix(self.h_n,1,0.0)
#o_o是预测值,第i个样本的预测值
self.o_o = self.utils.create_matrix(self.o_n,1,0.0)
#初始化连接权值矩阵
self.w_i_h = self.utils.create_random_matrix(self.i_n,self.h_n,0.2)
self.w_h_o = self.utils.create_random_matrix(self.h_n,self.o_n,2)
#delta
self.o_delta = self.utils.create_matrix(self.o_n, 1,0.0)
self.h_delta = self.utils.create_matrix(self.h_n, 1,0.0)
#delta w和,batch_size个样本的训练的和,也就是批量更新
self.w_h_o_delta = self.utils.create_matrix(self.h_n,self.o_n,0.0)
self.w_i_h_delta = self.utils.create_matrix(self.i_n,self.h_n,0.0)
#训练
def train(self,hidden_activation,output_activation,train_inputs,train_outputs,alpha,error_threshold,iteration_num,batch_percent):
#隐含层的激活函数
self.h_activation = hidden_activation
#输出层的激活函数
self.o_activation = output_activation
#学习步长
self.alpha = alpha
#训练样本的个数
self.train_sample_n = np.shape(train_inputs)[0]
#这次迭代的总误差
self.train_error = 0.0
#误差阈值
self.error_threshold = error_threshold
#最大迭代次数
self.iteration_num = iteration_num
#每一次批量更新需要使用的样本个数
if batch_percent>100:
batch_percent = 100
self.batch_size = (int)(self.train_sample_n*batch_percent/100)
#训练样本输入,矩阵,每一行为一个样本特征
self.train_inputs = train_inputs
#训练样本真实值,矩阵,每一行为一个样本的值
self.train_outputs = train_outputs
#开始训练
self.batch()
#测试
def test(self,test_inputs,test_outputs=None):
#测试样本个数
self.test_sample_n = np.shape(test_inputs)[0]
#预测集合
predict_outputs = self.utils.create_matrix(self.test_sample_n, self.o_n,0.0)
for i in range(self.test_sample_n):
#预测第i个测试样本
self.predict(test_inputs[i:i+1:,::])
#预测结果在self.o_o中
predict_outputs[i:i+1:,::] = np.transpose(self.o_o)
print "actural: ",test_outputs[i]
'''
print "predict values:"
print predict_outputs
#如果测试样本有结果,则输出真实结果以及预测总误差
if test_outputs is not None:
diff = test_outputs-predict_outputs
self.test_error = 0.5*np.sum(np.sum(np.multiply(diff,diff),axis=1),axis=0)[0,0]
print "actural values:"
print test_outputs
print "test error:"
print self.test_error
'''
#预测一个样本
def predict(self,test_input):
#输入层的输出,即为其输入,i_nx1矩阵,因为有个偏置项,所有两个矩阵行数不一样,需要进行这样的赋值操作
self.i_o[0:self.i_n-1:,0:1:] = np.transpose(test_input[0:1:,::])
#计算隐含层每个节点的输出h_o
self.h_o = self.h_activation.f(np.transpose(self.w_i_h)*self.i_o)
#计算输出层每个节点的输出o_o
self.o_o = self.o_activation.f(np.transpose(self.w_h_o)*self.h_o)
print "predict: ",self.o_o
#批量更新
def batch(self):
#一次batch使用的样本的编号集
inputs_indexs = [i for i in range(self.batch_size)]
#下次batch的需要使用的第一个样本的编号
last_index = (inputs_indexs[-1]+1)%self.train_sample_n
#批量更新,直到误差小于阈值或者达到最大迭代次数
while True:
#print "inputs_indexs:",inputs_indexs
self.one_batch(inputs_indexs)
#print "error: ",self.train_error
#剩余的迭代次数减1
self.iteration_num -= 1
#判断误差是否不再改变或者达到最大迭代次数
if self.terminate():
break
else:#否则继续迭代
#得到下次batch所需要使用的样本集所对应的编号集
'''
举例:训练样本集所对应的编号集是[0,1,2,3,4,5],样本个数为6,即train_sample_n=6
如果batch_size=4,即每一次batch使用四个样本,
那么第一次使用的batch样本集所对应的编号集inputs_indexs=[0,1,2,3]
last_index = 4
第二次使用的batch样本集所对应的编号集inputs_indexs=[4,5,0,1]
即以后每次batch的inputs_indexs为:
for i in range(self.batch_size):
inputs_indexs.append((i+last_index)%self.train_sample_n)
'''
inputs_indexs = []
for i in range(self.batch_size):
inputs_indexs.append((i+last_index)%self.train_sample_n)
last_index = (inputs_indexs[-1]+1)%self.train_sample_n
#一次batch
def one_batch(self,inputs_indexs):
#对每一个样本,首先使用前向传递,然后使用误差反向传播
for i in inputs_indexs:
#前向传递
self.fp(i)
#break
#反向传播
self.bp(i)
#更新权值
self.update()
#第i个样本前向传递
def fp(self,i):
#输入层的输出,即为其输入,第i个样本, i_nx1矩阵
self.i_o[0:self.i_n-1:,0:1:] = np.transpose(self.train_inputs[i:i+1:,::])
#计算隐含层每个节点的输入h_i,以及隐含层的输出h_o
self.h_i = np.transpose(self.w_i_h)*np.matrix(self.i_o)
self.h_o = self.h_activation.f(self.h_i)
#计算输出层每个节点的输入o_i,以及隐含层的输出o_o
self.o_i = np.transpose(self.w_h_o)*self.h_o
self.o_o = self.o_activation.f(self.o_i)
#计算平方误差和
actural = np.transpose(self.train_outputs[i:i+1:,::])
tmp = self.o_o-actural
self.train_error = self.train_error + (np.transpose(tmp)*tmp)[0,0]
#第i个样本误差反向传播
def bp(self,i):
#对输出层每一个节点,计算\Delta_{ij}^{T-1}=(y_{ij}-\hat{y}_{ij}) \cdot f'^{T}(v)|_{v=I_{ij}^{T}}
self.o_delta = np.multiply((self.o_o-np.transpose(self.train_outputs[i:i+1:,::])),
self.o_activation.df(self.o_i))
#print "self.o_delta:",self.o_delta
#使用公式\frac{1}{p}\sum_{i=1}^{p}\Delta_{ij}^{T-1} \cdot o^{T-1}_{ik}计算\Delta {w_{kj}^{T-1}}
#前面的系数frac{1}{p}还没乘
self.w_h_o_delta = self.w_h_o_delta + self.h_o*np.transpose(self.o_delta)
#print "self.w_h_o_delta:",self.w_h_o_delta
#对隐含层每一个节点,计算\Delta_{ij}^{T-2}=\sum_{s=1}^{s_{T}}(y_{is}-\hat{y}_{is}) \cdot f'^{T}(v)|_{v=I_{is}^{T}}\cdot w_{js}^{T-1} \cdot f'^{T-1}(v)|_{v=I_{ij}^{T-1}}
self.h_delta = np.multiply(self.w_h_o*np.multiply((self.o_o-np.transpose(self.train_outputs[i:i+1:,::])),self.o_activation.df(self.o_i)),self.h_activation.df(self.h_i))
#print "self.h_delta:",self.h_delta
#使用公式\frac{1}{p}\sum_{i=1}^{p}\Delta_{ij}^{T-2}\cdot o^{T-2}_{ik}计算\Delta {w_{kj}^{T-2}}
#前面的系数frac{1}{p}还没乘
self.w_i_h_delta = self.w_i_h_delta + self.i_o*np.transpose(self.h_delta)
#print "self.w_i_h_delta:",self.w_i_h_delta
#更新权值W
def update(self):
#按照公式更新输入层与隐含层之间的w: w^{T-2}_{kj}:=w^{T-2}_{kj}-\alpha\frac{1}{p}\sum_{i=1}^{p}\Delta_{ij}^{T-2}\cdot o^{T-2}_{ik}
self.w_i_h = self.w_i_h - self.alpha/self.batch_size*self.w_i_h_delta
#按照公式更新隐含层与输出层之间的w: w^{T-1}_{kj}:=w^{T-1}_{kj}-\alpha\frac{1}{p}\sum_{i=1}^{p}\Delta_{ij}^{T-1} \cdot o^{T-1}_{ik}
self.w_h_o = self.w_h_o - self.alpha/self.batch_size*self.w_h_o_delta
#delta清零
self.w_i_h_delta = Utils().matrix_fill_zeros(self.w_i_h_delta)
self.w_h_o_delta = Utils().matrix_fill_zeros(self.w_h_o_delta)
#判断迭代是否终止
def terminate(self):
if(0.5*self.train_error/self.batch_sizeor self.iteration_num<=0):
return True
else:
print "error: ",self.train_error
self.train_error = 0.0
return False
if __name__=="__main__":
'''
inputs = np.matrix([[0,0],[0,1],[1,0],[1,1]])
outputs = np.matrix([[0],[1],[1],[0]])
bpnn = BPNN(2, 5, 1)
bpnn.train(Tanh(), Tanh(), inputs,
outputs, 0.1, 0.001,
10000, 100)
bpnn.test(inputs)
'''
#读取数据
r_fp = open("data","r")
#输入层节点数
input_level_node_num = 0
#隐藏层层节点数
hidden_level_node_num = 0
#输出层节点数
output_level_node_num = 0
#输入数据
inputs = []
#数据的真实值
outputs = []
i = 0
for line in r_fp:
strs = line.strip().split(",")
#第一行是每层的节点数
if i==0:
input_level_node_num = int(strs[0])
hidden_level_node_num = int(strs[1])
output_level_node_num = int(strs[2])
else:
#数据,最后一列是真实值
#特征值向量
i_v = []
#真实值向量
o_v = []
for i in range(len(strs)-1):
i_v.append(float(strs[i]))
o_v.append(float(strs[-1]))
inputs.append(i_v)
outputs.append(o_v)
i+=1
inputs = np.matrix(inputs)
outputs = np.matrix(outputs)
#每个特征以及结果的的最大值最小值归一化
max_inputs = np.max(inputs,axis=0)
min_inputs = np.min(inputs,axis=0)
normalize_inputs = (inputs-min_inputs)/(max_inputs-min_inputs)
max_outputs = np.max(outputs,axis=0)
min_outputs = np.min(outputs,axis=0)
normalize_outputs = (outputs-min_outputs)/(max_outputs-min_outputs)
#获取总共样本的个数
smaple_n = np.shape(normalize_inputs)[0]
#将数据按照2:1拆分成训练集与测试集
train_sample_n = smaple_n*2.0/3
train_inputs = normalize_inputs[0:train_sample_n:1,::]
train_outputs = normalize_outputs[0:train_sample_n:1,::]
test_inputs = normalize_inputs[train_sample_n:smaple_n:1,::]
test_outputs = normalize_outputs[train_sample_n:smaple_n:1,::]
#构建网络
bpnn = BPNN(input_level_node_num, hidden_level_node_num, output_level_node_num)
#训练
bpnn.train(Sigmoid(), Sigmoid(), train_inputs,
train_outputs, 0.2, 0.01,
1000, 100)
#测试,其实最后预测值需要进行反归一化,这里没有做此步骤
bpnn.test(test_inputs,test_outputs)