sklearn ROC曲线使用

这篇文章中我将使用sklearn的ROC曲线官方示例代码进行讲解，当然主要目的还是在于记录，好记性不如烂键盘嘛。

ROC曲线定义

ROC曲线是Receiver Operating Characteristic Curve的简称，中文名为“受试者工作特征曲线”。
ROC曲线的横坐标为假阳性率（False Positive Rate，FPR）；纵坐标为真阳性率（True Positive Rate，TPR）。FPR和TPR的计算方法分别为：
$$FPR=\frac{FP}{FP+TN}$$
$$TPR=\frac{TP}{TP+FN}$$
式中FP表示实际为负但被预测为正的样本数量，TN表示实际为负被预测为负的样本的数量，TP表示实际为正被预测为正的样本数量，FN表示实际为正但被预测为负的样本的数量。这几个变量可以用下面的混淆矩阵表示：

从混淆矩阵也可以看到FP+TN是实际为负的样本数量，因此，FPR公式也可以写作：
$$FPR=\frac{FP}{N}$$
同理，TP+FN是实际为正的样本数量，因此，TPR公式也可以写作：
$$TPR=\frac{TP}{T}$$
ROC曲线上的每个点的横坐标就是FPR，纵坐标就是TPR。

绘制ROC曲线

假设我们有一个二分类器，分类器对所有的样本进行分类并给出一个0,1之间的分数，一般来说我们会设置一个阈值，大于这个阈值则将其预测为正，小于该阈值即预测为负，这样就可以得到混淆矩阵中的各个值，从而得到一组(FPR, TPR)。
问题在于，通常一个分类器的阈值只有一个，这样才可以确定谁正谁负。但这样也只有一组(FPR, TPR)，而绘制ROC曲线需要很多组这样的点才可以，那么我们该如何得到它呢？
我们结合下面的样本看一下：

我们将所有的样本按照预测分数从高到低进行排序，然后以每个预测分数为阈值确定一组（FPR，TPR）。比如说，当将预测分数0.85作为阈值时，那么序号为1，2，3的三个样本被预测为正，其余被预测为负，再利用每个样本的实际类别确定混淆矩阵，从而得到FPR为$\frac{1}{6}$，TPR为$\frac{1}{2}$，以此类推就可以得到多组(FPR, TPR)从而得到绘制ROC曲线需要的数据了。
ROC曲线上比较特殊的点是当阈值为1时，即(FPR, TPR)为(0, 0)的点，当阈值为0时的(1, 1)点。
另外，在ROC曲线中有一条特殊的线，即FPR=TPR的线，这条线对应的分类器等价于随机猜测，因为二分类问题是有一半的概率随机猜对的。
好的分类器的ROC曲线是位于FPR=TPR曲线的上方的。而完美的分类器是FPR等于0，TPR为1的那点所对应的分类器。一般来说，分类器越接近于(0, 1)点，其分类器性能越好。
对于ROC曲线位于FPR=TPR线之下的分类器也不是一无是处，我们只需按照其预测结果反着来就可以得到较好的分类器了。
其实，还有一种更直观地绘制ROC曲线的方法，我们简短的说一下。首先，根据样本标签统计出正负样本的数量，假设正样本数量为P，负样本数量为N；接下来，把横轴的刻度间隔设置为1/N，纵轴的刻度间隔设置为1/P；再根据模型输出的预测概率对样本进行排序（从高到低）；依次遍历样本，同时从零点开始绘制ROC曲线，每遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线，每遇到一个负样本就沿横轴方向绘制一个刻度间隔的曲线，直到遍历完所有样本，曲线最终停在(1, 1)这个点，整个ROC曲线绘制完成。

AUC定义

AUC（Area Under Curve）就是ROC曲线下的面积大小，它能够量化地反映基于ROC曲线衡量出的模型性能。AUC的取值一般在0.5和1之间，AUC越大，说明分类器越可能把实际为正的样本排在实际为负的样本的前面，即正确做出预测。

代码讲解

官方示例的链接为Receiver Operating Characteristic (ROC)

二分类

import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle

from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp

# 导入鸢尾花数据集
iris = datasets.load_iris()
X = iris.data  # X.shape==(150, 4)
y = iris.target  # y.shape==(150, )

# 二进制化输出
y = label_binarize(y, classes=[0, 1, 2])  # shape==(150, 3)
n_classes = y.shape[1]  # n_classes==3

# 添加噪音特征，使问题更困难
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape  # n_samples==150, n_features==4
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]  # shape==(150, 84)

# 打乱数据集并切分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5,
                                                    random_state=0)
# X_train.shape==(75, 804), X_test.shape==(75, 804), y_train.shape==(75, 3), y_test.shape==(75, 3)

# 学习区分某个类与其他的类
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,
                                 random_state=random_state))
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# y_score.shape==(75, 3)

# 为每个类别计算ROC曲线和AUC
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])
# fpr[0].shape==tpr[0].shape==(21, ), fpr[1].shape==tpr[1].shape==(35, ), fpr[2].shape==tpr[2].shape==(33, ) 
# roc_auc {0: 0.9118165784832452, 1: 0.6029629629629629, 2: 0.7859477124183007}

plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

上述代码得到的图像如下图所示，代码中只画出了第三个分类器的ROC曲线。

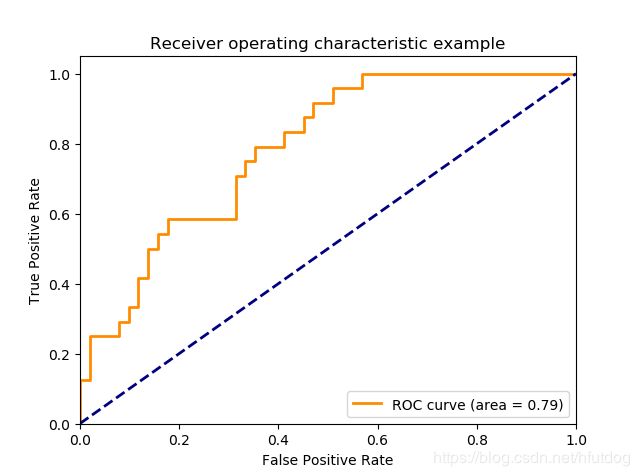
我将上述代码的注释改为中文，并将一些步骤的输出也写在了注释中。
fpr2的shape为(35, )，说明上述ROC曲线是由37组(FPR, TPR)绘制出来的（含(0, 0)和(1, 1)点）。问题在于，我们使用的不是75条数据作为预测集吗？为什么最终只剩35个值了呢？一个原因在于，roc_curve方法的参数drop_intermediate默认设置为True，也就是说每组的阈值并不是将所有的值取满的，它删除了一些次优的阈值；还有一个原因可能是75条数据预测出的分数中有重复的，那么阈值数量也就变少了。
代码中roc_auc的值为{0: 0.9118165784832452, 1: 0.6029629629629629, 2: 0.7859477124183007}，它们就是三个类别的二分类器的AUC值，可以看到上图中area=0.79是与roc_auc第三个值相对应的。

多分类

将二分类的代码从plt.figure()行开始替换成如下代码就可以得到多分类的ROC曲线。

# 计算微平均ROC曲线和AUC
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

# 计算宏平均ROC曲线和AUC

# 首先汇总所有FPR
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))

# 然后再用这些点对ROC曲线进行插值
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
    mean_tpr += interp(all_fpr, fpr[i], tpr[i])

# 最后求平均并计算AUC
mean_tpr /= n_classes

fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])

# 绘制所有ROC曲线
plt.figure()
lw = 2
plt.plot(fpr["micro"], tpr["micro"],
         label='micro-average ROC curve (area = {0:0.2f})'
               ''.format(roc_auc["micro"]),
         color='deeppink', linestyle=':', linewidth=4)

plt.plot(fpr["macro"], tpr["macro"],
         label='macro-average ROC curve (area = {0:0.2f})'
               ''.format(roc_auc["macro"]),
         color='navy', linestyle=':', linewidth=4)

colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):
    plt.plot(fpr[i], tpr[i], color=color, lw=lw,
             label='ROC curve of class {0} (area = {1:0.2f})'
             ''.format(i, roc_auc[i]))

plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()

上述代码的输出图像如下所示：

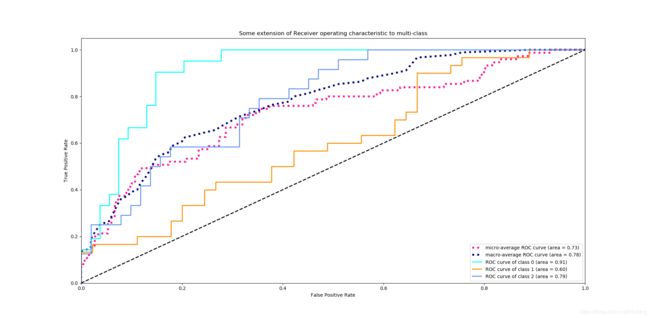
代码中涉及到interp()函数，可以参考我的这篇文章：numpy.interp()用法。
从代码中我们可以看到多分类的ROC曲线包括微平均（micro-average）ROC曲线和宏平均（macro-average）ROC曲线，我们只要明白了两种曲线的绘制方式就很容易看懂上面的代码。
在具体看两种曲线之前，我们先定义两个矩阵。一个是标签矩阵L（即各样本的实际类别），一个是概率矩阵P（即分类器预测的各样本类别）。两种矩阵的形状都是m行n列，其中m为样本个数，n为样本的类别个数，两个矩阵中样本和类别顺序都是互相对应的。标签矩阵L是二进制矩阵，矩阵中的一行表示某个样本是否属于各个类别（例如0表示“不属于该类别”，1表示“属于该类”）。概率矩阵P和标签矩阵L每个元素一一对应，只不过现在用0和1之间的概率值表示分类器的预测结果，矩阵中的一行表示某个样本属于各个类别的概率。

• 微平均ROC曲线：
  假设每个样本只属于多个类别中的某个类别。在标签矩阵L中元素1表示样本的类别，0表示样本不属于该类。那么在概率矩阵P中，如果分类器对某个样本的预测结果是正确的，对应该样本的概率矩阵的行中最大的元素就对应标签矩阵L中值为1的类别。
  微平均的做法是将标签矩阵L和概率矩阵P按行展开（对应代码中的y_test.ravel(), y_score.ravel()），然后将两个行向量转置合并，就得到一个两列的矩阵。这个矩阵相当于m*n个样本的二分类
  结果，一列为实际的类别，另外一列为预测类别。这样就可以按照二分类计算ROC的方式得到多分类的ROC曲线了（对应程序中的前两行）。
• 宏平均ROC曲线：
  取标签矩阵L和概率矩阵P中的对应两列，就构成了一个二分类的实际类别和预测结果，这样就可以得到一条ROC曲线（某个类别下的FPR和TPR）。依次取完各个类别就可以得到多条ROC曲线，然后将所有ROC曲线取平均就得到宏平均ROC曲线了。
  需要注意的是，两种方法得到的ROC曲线是不同的，因此AUC也是不同的。

总结

ROC曲线的特点在于当测试集中的正负样本的分布发生变化时，ROC曲线的形状能够基本保持不变。这个特点让ROC曲线能够降低不同测试集带来的干扰，更加客观地衡量模型本身的性能。ROC曲线被广泛用于排序、推荐、广告等领域。

参考

机器学习之分类性能度量指标 : ROC曲线、AUC值、正确率、召回率
ROC原理介绍及利用python实现二分类和多分类的ROC曲线
《百面机器学习》（诸葛越主编、葫芦娃著）第二章第2节——ROC曲线