AlphaGo Zero是如何工作的?——AlphaGo Zero背后的强化学习算法原理
Deepmind公司的AlphaGo算法是第一个打败人类选手的围棋程序。2016年三月,打败李世石的是AlphaGo Lee,一个靠大量人类围棋专家的棋谱进行监督学习和自对弈强化学习进行训练的AI程序。不久之后,deepmind的新论文展示了不同于之前AlphaGo的全新网络结构——它仅仅用了三天的自对弈强化学习而无需人类的下棋经验就以100-0的战绩打败了AlphaGo。它就是大名鼎鼎的AlphaGo Zero。这篇文章将介绍AlphaGo Zero背后的算法原理。
其他资料可以参考我的另外两篇
一张图读懂AlphaGo Zero背后的强化学习算法原理
AlphaGo Zero强化学习简易教程
蒙特卡洛树搜索
蒙特卡洛树搜索(Monte Carlo Tree Search)可以说是棋类游戏机器人的入门级算法了。它适合处理离散的、确定性的、完全信息的(perfect information,也就是双方都能看到完全的棋局状态)棋类游戏。当一个机器人开始下棋,最简单的方法就是把所有可能的结果全部尝试一遍,这样就能得到对手所有可能的应对措施,以及下一步应该走哪等等。但是像围棋这样的游戏,动作搜索空间将随着棋局的进行变得越来越庞大,以至于暴力穷举变得极不现实。而蒙特卡洛树搜索可以有选择地尝试它觉得不错的可选动作,如此就将大部分算力集中于最有可能性的走子方案上,使搜索变得高效。
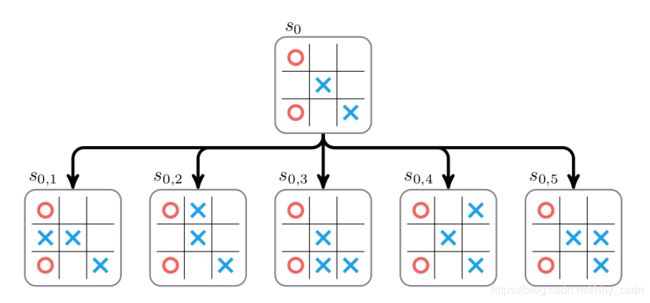
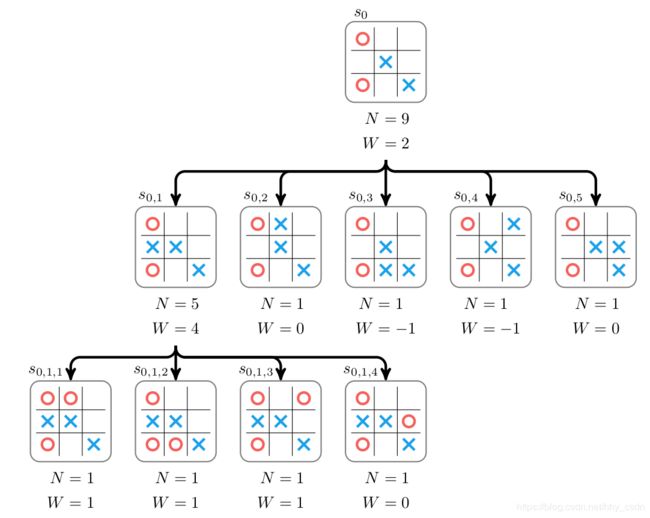
我们来具体地看一下MCTS的工作原理,以一字棋(tic-tac-toe)为例来说明。假设游戏的初始状态是 s 0 s_0 s0,轮到程序走子,走子的可选方案是一个动作集合 A A A。蒙特卡洛搜索树初始化为一个只含有单结点 s 0 s_0 s0的树。下面,搜索算法对状态 s 0 s_0 s0下的每一个可能的走子方案 a ∈ A a\in A a∈A都尝试一次,建立了五个子结点,分别是 s 0 , 1 , s 0 , 2 , s 0 , 3 , s 0 , 4 , s 0 , 5 s_{0,1},s_{0,2},s_{0,3},s_{0,4},s_{0,5} s0,1,s0,2,s0,3,s0,4,s0,5。
接着从每个子结点出发,采用随机走子策略完成当前棋局(rollout),确定 s 0 → s 0 , i s_0 \rightarrow s_{0,i} s0→s0,i的动作价值。若MCTS算法一方赢得棋局,这个子结点记为 + 1 +1 +1,输掉为 − 1 -1 −1,平局记为 0 0 0。(多说一句,如果从 s 0 , i s_{0,i} s0,i出发,经过足够多次simulation,则累计回报的平均值就可以评价这个状态 s 0 , i s_{0,i} s0,i的好坏了)
我们假设从 s 0 , 1 s_{0,1} s0,1结点出发,赢得棋局,得到价值函数的估计值 + 1 +1 +1,但是这个值并不代表下一次走这个方案还会赢,它取决于从 s 0 , 1 s_{0,1} s0,1出发的rollout采取什么样的走子策略完成棋局。从子结点出发,可以采用完全随机的、非智能的走子策略,也可以采取更优秀的随机策略,也可以从 s 0 , 1 s_{0,1} s0,1直接估计价值函数(比如利用神经网络)。
上图我们画出来从 s 0 s_0 s0根结点出发,探索了五个子结点的情况。每个结点存储两个变量:
-
N N N表示访问该结点 s 0 , i s_{0,i} s0,i或该结点的子结点 s 0 , i , j s_{0,i,j} s0,i,j的次数。也就是说,在该结点 s 0 , i s_{0,i} s0,i的子结点执行simulation的次数也要在信息回传过程中加到 N s 0 , i N_{s_{0,i}} Ns0,i上,我们之后会讲到回传是怎样进行的。
-
W W W代表累计回报值,将从该结点出发的所有simulation的回报值加起来就是 W W W。
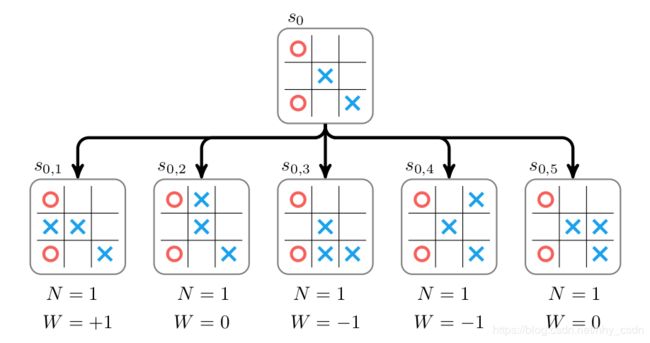
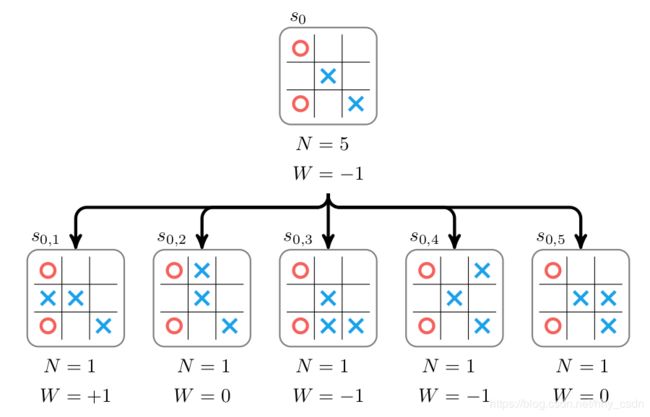
当探索完子结点,就需要把子结点记录的信息回传给它的上级结点。如下图所示,子结点 { s 0 , i , ∣ i = 1 , ⋯ , 5 } \{s_{0,i},\mid \ i=1,\cdots,5\} {s0,i,∣ i=1,⋯,5}分别探索一次,获得回报分别是 { + 1 , 0 , − 1 , − 1 , 0 } \{ +1,0,-1,-1,0 \} {+1,0,−1,−1,0},则上级节点 s 0 s_0 s0的访问次数加5,累计回报价值为 1 + 0 − 1 − 1 + 0 = − 1 1+0-1-1+0=-1 1+0−1−1+0=−1。
蒙特卡洛树搜索的基本流程就是这样:1)选择一个结点,2)以上述方式扩展该结点——执行可能的动作,并将游戏进行到底以获得最终分数即回报价值,3)将该结点的信息回传给它的上级,并不断地重复这一过程。但是MCTS不会扩展所有可能的子结点,这样做的计算代价非常之大。所以搜索算法在选择哪个结点向下扩展的时候会平衡两方面:选择当前较优的结点向下拓展(W值高)和选择较少探索过的结点(N值小),如果了解强化学习基本概念,就会发现这其实就是在平衡探索exploration和利用exploitation之间的关系。
MCTS算法怎样选择子结点呢?假设当前结点共有 M M M个子结点可供拓展,搜索树会选择具有最高上限置信区间(Upper Confidence Bound applied to Tree,UCT)的子结点:
U i = W i N i + c ln N p N i , i = 1 , ⋯ , M U_i=\frac{W_i}{N_i}+c\sqrt{\frac{\ln N_p}{N_i}},\ i=1,\cdots,M Ui=NiWi+cNilnNp, i=1,⋯,M
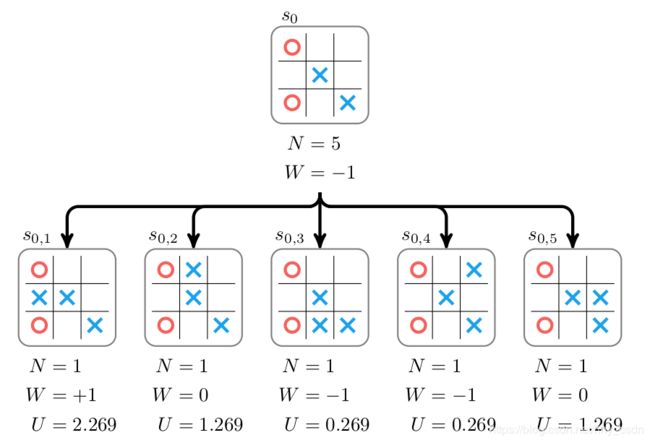
式中, W i W_i Wi是第 i i i个子结点的累计回报值, N i N_i Ni是第 i i i个子结点的访问次数, N p N_p Np是父节点的访问次数,其值等于所有子结点访问次数 N i N_i Ni之和。参数 c c c是控制探索和利用的超参数: c c c值小,则偏重于选择具有高平均回报值的子结点; c c c值大,则算法偏向于选择访问次数少的子结点。当取 c = 1 c=1 c=1的时候,上图的 U U U值计算如下:
五个子结点中,第一个结点的 U U U值最高,所以我们选择第一个结点 s 0 , 1 s_{0,1} s0,1向下拓展。并将 s 0 , 1 s_{0,1} s0,1结点之下的模拟结果反向传播至树的上层。
这里要注意,我们做rollout得到的 W W W值都是在反映 × \times ×棋的输赢,在选择结点时,如果轮到 ∘ \circ ∘棋,就需要将 W W W值取反,因为零和游戏的双方看待棋局的好坏是截然相反的。
在时间没有溢出的情况下,MCTS算法不断地在 s 0 s_0 s0的子结点下进行rollout模拟。最终搜索树被完全拓展开,理想状态下,搜索树探索了所有可能的动作(导致的子结点),于是就能反映出最值得采取的动作是什么。假设搜索了足够多次后,树的状态如下,则应该选择平均回报值最大(51/106=0.48)的第一个子结点,在那个位置上真实地下一个棋子,棋局的状态也就随之转移到 s 0 , 1 s_{0,1} s0,1,这时我们完成了一步棋的搜索,再走下一步时,就以 s 0 , 1 s_{0,1} s0,1为根节点建立搜索树,搜索足够次数并选择最优。
使用专家策略提升搜索效率
围棋和象棋这样的棋类游戏在进行树搜索时有着非常庞大的分支,在某个状态下可执行的动作也非常多,所以搜索起来非常困难。据计算,在象棋中大约有 1 0 46 10^{46} 1046种状态,而一个 19 × 19 19\times 19 19×19的围棋棋盘上大约有 1 0 170 10^{170} 10170种状态,相比之下,一字棋只有5478个不同棋盘状态。
用普通的MCTS算法进行策略评估Policy Evaluation——或者叫走子评估Move Evaluation(即第一部分所述内容)——还是不够高效,我们需要搜索树把搜索精力尽量集中在更有价值的走子方案上。
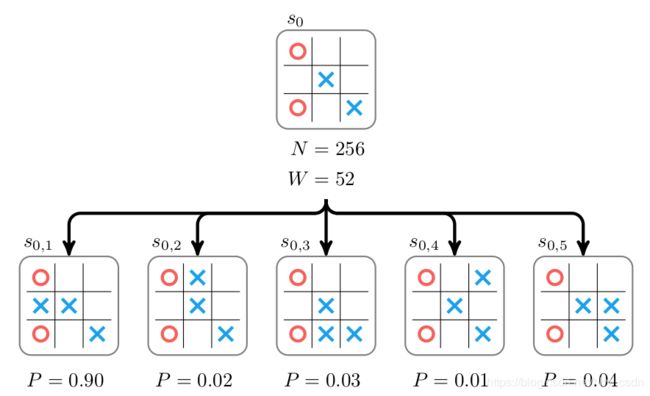
我们假设有一个专家策略 π \pi π,对于一个给定状态 s s s,策略 π \pi π能给出专业水平的选手可能的走子方案。以一字棋为例:如下图所示, P i = π ( a i ∣ s 0 ) P_i=\pi(a_i\mid s_0) Pi=π(ai∣s0)是在状态 s 0 s_0 s0下采取第 i i i个动作 a i a_i ai的条件概率。
如果这个专家策略足够强大,我们就可以直接根据策略 π \pi π的指导走下一步棋,或者说,选择 arg m a x a i { P i = π ( a i ∣ s ) } \arg max_{a_i}\{ P_i=\pi(a_i\mid s) \} argmaxai{Pi=π(ai∣s)}作为下一步棋。但是,要得到专家策略 π \pi π也是蛮困难的事,要确定一个策略是最优的也几乎是不可能的。
幸运的是,我们可以用一种改进的MCTS算法逐步地优化一个策略。改进MCTS算法会在搜索树的每个结点额外存储动作条件概率,也就是上述 P i P_i Pi,概率值将在选择结点时起到作用。因此,Deepmind论文中采用的概率化的上限置信区间公式为
U i = W i N i + c ⋅ P i ln N p 1 + N i U_i=\frac{W_i}{N_i}+c\cdot P_i\sqrt{\frac{\ln N_p}{1+N_i}} Ui=NiWi+c⋅Pi1+NilnNp
与之前的UCT公式一样, U U U值在高回报值和低访问次数之间取平衡。但是在上式中,探索这一项还受到概率值的影响,也就是说,如果一个子结点没有或很少访问到,而且策略 π \pi π认为采取动作(从父结点转移到该子结点)的概率值较高,那它则更有可能被选中。如果专家策略 π \pi π下棋水平很高,那么搜索树就可以高效地估计当前棋盘状态。但如果这个专家策略水平不太高,那么搜索树对状态的估计就有偏差了。不管怎样,只要模拟的次数足够多,每个结点的访问次数足够多,结点的 U U U值就主要受输赢比率 W i N i \frac{W_i}{N_i} NiWi的控制,这和上一个公式是一样的。
提高 值估计 的效率
在上文说到,搜索树对每个结点进行 W W W值估计的时候,采用的方法是:从该结点出发,采用随机走子策略,完成一盘棋局(这个方法叫rollout),赢了记1分,输了记-1分,平局记0分。这个完全随机的方法看起来并不高效,也不准确。我们的第二个改进措施就从 随机rollout 着手。
第一个方案是采用之前所述的专家策略 π ( a ∣ s ) \pi(a\mid s) π(a∣s),去指导rollout的走子。即走子策略不再完全随机。如果 π \pi π比较优秀,rollout就能反应更多的真实情况,正确的估计状态的好坏;如果 π \pi π水平不高,在它的指导下从状态 s s s出发进行的模拟也就很难反映 s s s的好坏情况。
第二个方案是不直接进行rollout,而是采用值估计函数 W ^ ( s ) \hat{W}(s) W^(s)直接估计state value,不再将棋局从状态 s s s下完。 W ^ ( s ) \hat{W}(s) W^(s)采取当前状态 s s s作为输入,返回一个 [ − 1 , 1 ] [-1,1] [−1,1]的实数,反映了当前状态的好坏。如果 W ^ ( s ) \hat{W}(s) W^(s)对真实值的估计能力不错,那我们就可以在不执行rollout的情况下保持预测精度,提高值估计value estimate的效率。
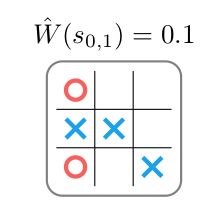
事实上,这两个方法可以同时运用,比如使用expert policy先模拟几个回合,到达状态 s ′ s' s′,而后再用 W ^ ( s ′ ) \hat{W}(s') W^(s′)得到状态 s s s的值估计。但是这两个方法都存在一个问题没有解决,那就是如何得到一个优秀的策略或是值估计函数?或者说,有没有一个算法能够对策略 π \pi π或函数 W ^ ( s ) \hat{W}(s) W^(s)进行训练呢?
AlphaZero中的神经网络
我们已经知道,AlphaZero采用改进的MCTS算法,通过自对弈的方式进行学习,可以一步一步地得到越来越好的策略 π \pi π和值估计函数 W ^ \hat{W} W^。在AlphaZero中,策略和值估计函数都是以深度神经网络的形式存在的。实际上,为了提高效率,AlphaZero采用了一个神经网络,同时给出下一步棋的动作概率和当前状态的价值。 p \bm{p} p形如 [ 0 , 0 , 0.1 , 0 , 0.3 , 0.4 , 0.2 , 0 ] [0,0,0.1,0,0.3,0.4,0.2,0] [0,0,0.1,0,0.3,0.4,0.2,0]。
f ( s ) → [ p , W ] f(s)\rightarrow[{\rm \bm{p}} ,\bm{W}] f(s)→[p,W]
值得注意的是,神经网络将最后8个回合的棋盘状态拆成黑白双方( 8 × 2 = 16 8\times2=16 8×2=16个 19 × 19 19\times19 19×19的棋局矩阵)和一个 19 × 19 19\times19 19×19的全0或全1矩阵(指示轮到黑白哪方)作为输入,输入的维度是 19 × 19 × 17 19\times19\times17 19×19×17。
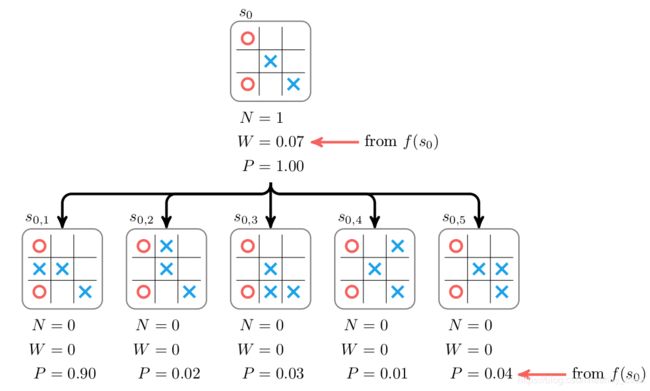
估计结点 s 0 s_0 s0的价值 W W W的rollout方法被神经网络 f ( s ) f(s) f(s)代替了。首先,初始化 s 0 s_0 s0的每个子结点的 N = 0 N=0 N=0和 W = 0 W=0 W=0。其次,走子概率 P P P由神经网络进行预测,如下图所示。五个可选动作的概率分别是 0.9 , 0.02 , 0.03 , 0.01 , 0.04 0.9,0.02,0.03,0.01,0.04 0.9,0.02,0.03,0.01,0.04。然后,状态 s 0 s_0 s0的 W W W值也由 f ( s 0 ) f(s_0) f(s0)得到。最后,根据 U U U值计算公式选择子结点向下扩展。结点信息的回传机制和之前一样。
我们说完了AlphaZero是怎么引入神经网络来完成前述的MCTS算法的。下面就来说一说AlphaZero的神经网络是怎么训练的。
AlphaZero的核心思想就是一个不断迭代、不断优化的神经网络。并且,利用MCTS算法进行的棋局走子数据也会作为网络训练的数据而收集起来。
具体的训练是这样的:网络的策略预测部分,状态 s 0 s_0 s0下,网络的输出 P s 0 ^ \hat{P_{s_0}} Ps0^被要求拟合MCTS算法经过搜索得到的概率 π s 0 \pi_{s_0} πs0,即
π i = N i 1 / τ \pi_i=N^{1/\tau}_i πi=Ni1/τ
τ \tau τ是温度系数, τ → 0 \tau\rightarrow0 τ→0表示选择状态 s 0 s_0 s0的访问次数最多(best move)的子结点, τ → ∞ \tau\rightarrow \infin τ→∞则表示策略 π \pi π趋近于完全随机。
值函数估计部分的训练目标是逼近真实的棋局结果 Z Z Z(输/赢/平),即从状态 s 0 s_0 s0预测这盘棋的输赢可能性,可以认为这是一个回归问题。
加入正则化项的总损失函数如下,式中 ( W − Z ) 2 (W-Z)^2 (W−Z)2是值估计的损失, π T ln P \pi^T\ln {\rm P} πTlnP是策略预测的交叉熵损失, λ ∥ θ ∥ 2 2 \lambda \| \theta \|^2_2 λ∥θ∥22是网络参数 θ \theta θ的正则化项。
( W − Z ) 2 + π T ln P + λ ∥ θ ∥ 2 2 (W-Z)^2+\pi^T\ln {\rm P}+\lambda \| \theta \|^2_2 (W−Z)2+πTlnP+λ∥θ∥22
在自对弈(self-play)阶段中,当前神经网络已经完成参数的更新,网络参数被固定住。(如果是第一次迭代,网络的参数为随机初始化。)当前网络被用来指导MCTS算法进行子结点的选择和扩展、结点的 W W W值估计和走子策略的预测等。具体来说,在每一局棋中,每走一步都经过若干次树搜索,得到策略 π ( a ∣ s ) \pi(a|s) π(a∣s)和棋局输赢信息 Z Z Z,这些数据以 ( s t , a t , r t ) (s_t,a_t,r_t) (st,at,rt)的形式收集起来,用于在网络训练阶段,做损失函数的随机梯度下降。